Deck 14: Integral Transform Method
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 14: Integral Transform Method
1
The solution of the integral equation 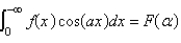 is
is
A)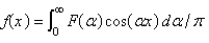
B)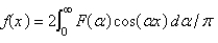
C)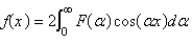
D)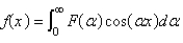
E) none of the above
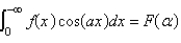 is
isA)
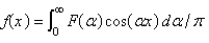
B)
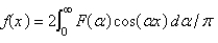
C)
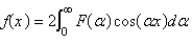
D)
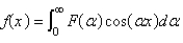
E) none of the above
B
2
In the three previous problems, the solution for 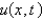 is
is
A)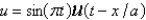
B)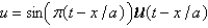
C)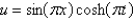
D)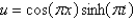
E)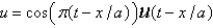
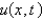 is
isA)
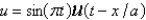
B)
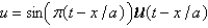
C)
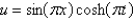
D)
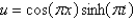
E)
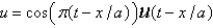
B
3
Let 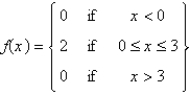 . The Fourier integral representation of f is
. The Fourier integral representation of f is
A)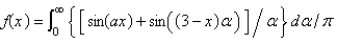
B)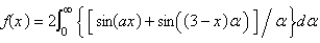
C)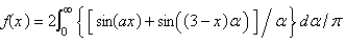
D)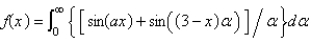
E) none of the above
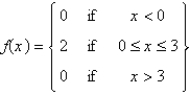 . The Fourier integral representation of f is
. The Fourier integral representation of f isA)
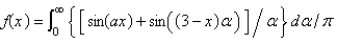
B)
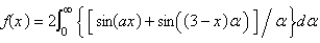
C)
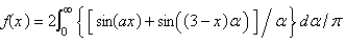
D)
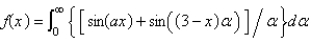
E) none of the above
C
4
In the previous problem, the solution for 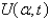 is
is
A)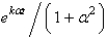
B)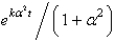
C)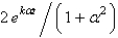
D)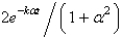
E)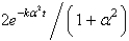
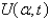 is
isA)
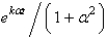
B)
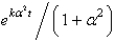
C)
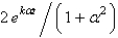
D)
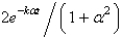
E)
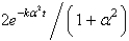

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
In the previous problem, the integral converges at 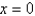 to the value
to the value
A) 0
B)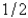
C) 1
D) 2
E)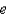
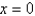 to the value
to the valueA) 0
B)
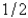
C) 1
D) 2
E)
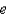

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
The value of 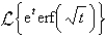 is
is
A)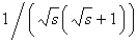
B)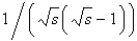
C)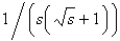
D)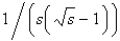
E) none of the above
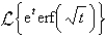 is
isA)
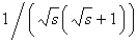
B)
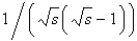
C)
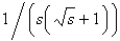
D)
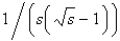
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
The value of 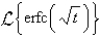 is
is
A)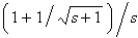
B)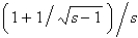
C)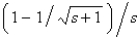
D)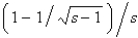
E) none of the above
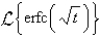 is
isA)
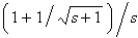
B)
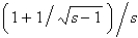
C)
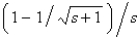
D)
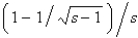
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
In the previous two problems, the integral converges for 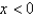 to the function
to the function
A)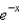
B)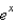
C)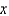
D) 1
E) none of the above
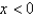 to the function
to the functionA)
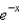
B)
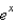
C)
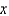
D) 1
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
In the previous three problems, the solution for 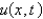 is
is
A)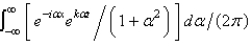
B)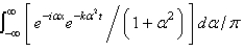
C)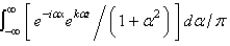
D)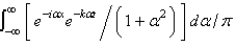
E)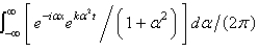
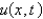 is
isA)
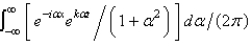
B)
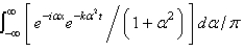
C)
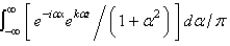
D)
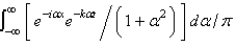
E)
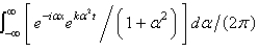

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
The complementary error function is defined as
A)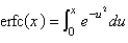
B)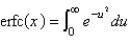
C)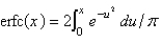
D)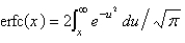
E)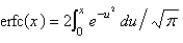
A)
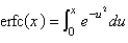
B)
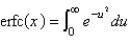
C)
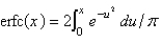
D)
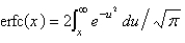
E)
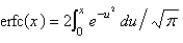

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
In the previous problem, assume that 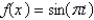 . The solution for
. The solution for 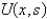 is
is
A)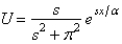
B)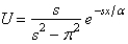
C)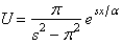
D)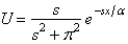
E)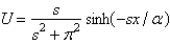
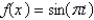 . The solution for
. The solution for 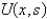 is
isA)
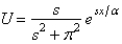
B)
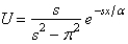
C)
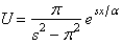
D)
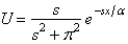
E)
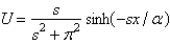

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
Apply a Fourier transform in 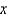 in the previous problem. The resulting equation for
in the previous problem. The resulting equation for 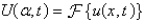 is
is
A)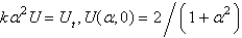
B)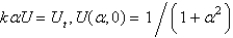
C)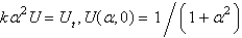
D)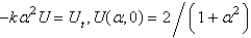
E)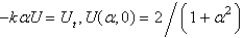
 in the previous problem. The resulting equation for
in the previous problem. The resulting equation for 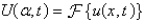 is
isA)
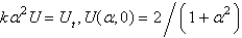
B)
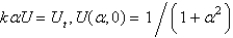
C)
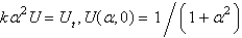
D)
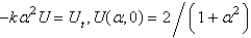
E)
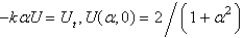

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
The Fourier cosine integral of a function f defined on 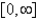 is
is
A)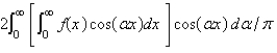
B)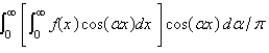
C)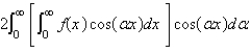
D)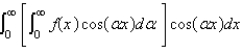
E)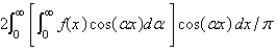
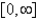 is
isA)
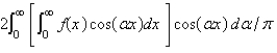
B)
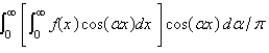
C)
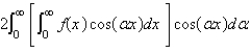
D)
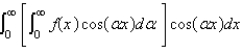
E)
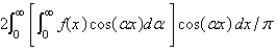

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
In the previous problem, the integral converges at 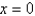 to the value
to the value
A) 0
B) 1
C) 2
D) 3
E) 4
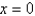 to the value
to the valueA) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
In the previous problem, if 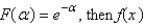 is
is
A)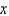
B)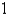
C)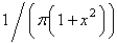
D)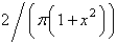
E) 0
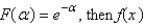 is
isA)
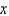
B)
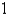
C)
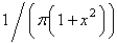
D)
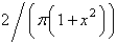
E) 0

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the temperature, 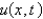 , in an infinite rod
, in an infinite rod 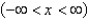 , with an initial temperature of
, with an initial temperature of 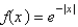 . The mathematical model for this is
. The mathematical model for this is
A)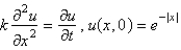
B)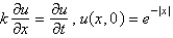
C)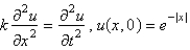
D)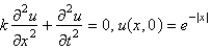
E)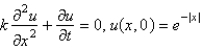
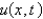 , in an infinite rod
, in an infinite rod 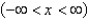 , with an initial temperature of
, with an initial temperature of 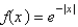 . The mathematical model for this is
. The mathematical model for this isA)
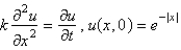
B)
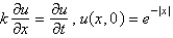
C)
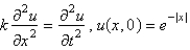
D)
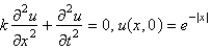
E)
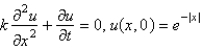

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
In the previous problem, apply the Laplace transform. The resulting equation for 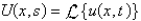 is
is
A)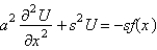
B)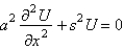
C)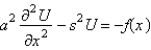
D)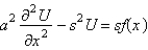
E)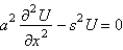
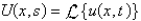 is
isA)
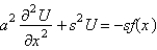
B)
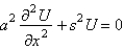
C)
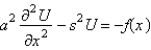
D)
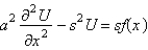
E)
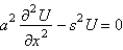

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
Consider a semi-infinite, elastic, vibrating string, with zero initial position and velocity, driven by a vertical force at 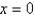 , so that
, so that 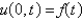 . Assume that
. Assume that 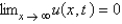 . The mathematical model for the deflection,
. The mathematical model for the deflection, 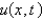 , is
, is
A)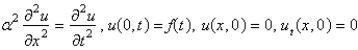
B)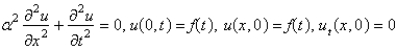
C)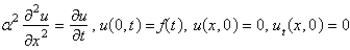
D)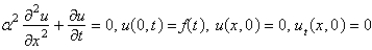
E)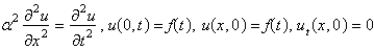
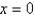 , so that
, so that 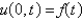 . Assume that
. Assume that 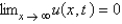 . The mathematical model for the deflection,
. The mathematical model for the deflection, 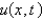 , is
, isA)
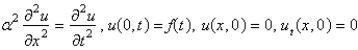
B)
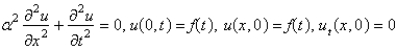
C)
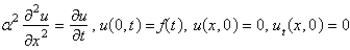
D)
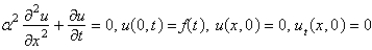
E)
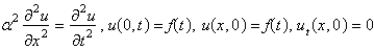

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
The value of 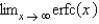 is
is
A) 0
B) 1
C)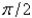
D)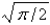
E)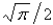
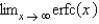 is
isA) 0
B) 1
C)
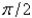
D)
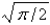
E)
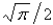

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
The Fourier cosine integral of 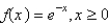 is
is
A)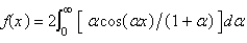
B)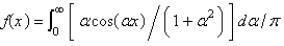
C)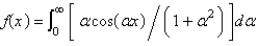
D)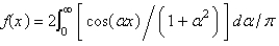
E)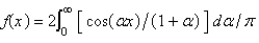
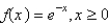 is
isA)
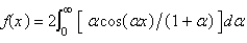
B)
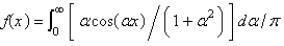
C)
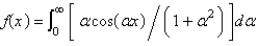
D)
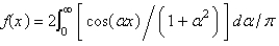
E)
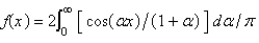

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
In the previous problem, assume that 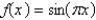 . The solution for
. The solution for 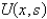 is
is
A)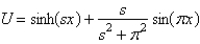
B)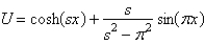
C)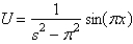
D)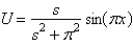
E)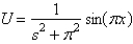
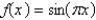 . The solution for
. The solution for 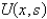 is
isA)
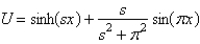
B)
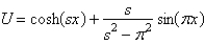
C)
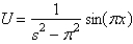
D)
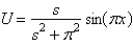
E)
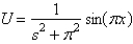

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
The value of 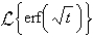 is
is
A)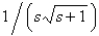
B)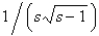
C)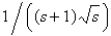
D)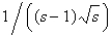
E) none of the above
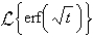 is
isA)
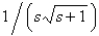
B)
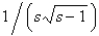
C)
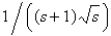
D)
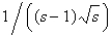
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The error function is defined as
A)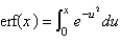
B)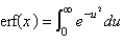
C)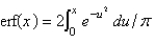
D)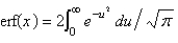
E)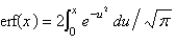
A)
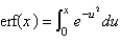
B)
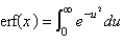
C)
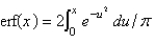
D)
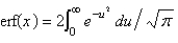
E)
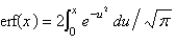

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the problem of finding the temperature in a semi-infinite rod with zero initial temperature and a fixed constant temperature, 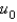 , at
, at 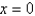 . The mathematical model for this problem is
. The mathematical model for this problem is
A)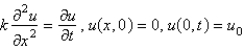
B)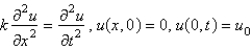
C)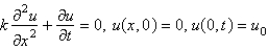
D)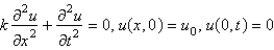
E)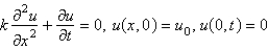
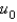 , at
, at 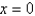 . The mathematical model for this problem is
. The mathematical model for this problem isA)
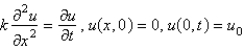
B)
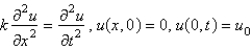
C)
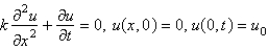
D)
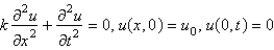
E)
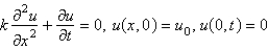

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The value of 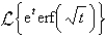 is
is
A)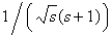
B)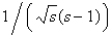
C)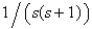
D)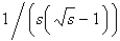
E)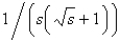
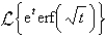 is
isA)
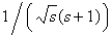
B)
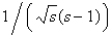
C)
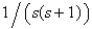
D)
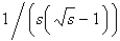
E)
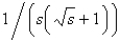

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
The value of 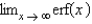 is
is
A) 0
B) 1
C)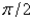
D)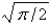
E)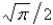
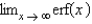 is
isA) 0
B) 1
C)
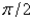
D)
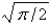
E)
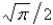

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
The Laplace transform of a function f is
A)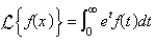
B)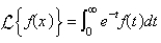
C)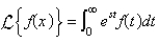
D)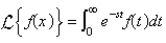
E)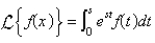
A)
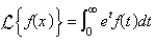
B)
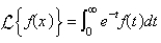
C)
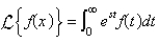
D)
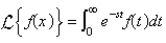
E)
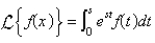

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
The Fourier integral representation of a function f is given by
A)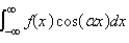
B)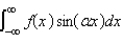
C)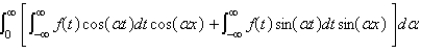
D)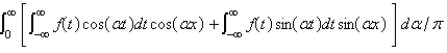
E)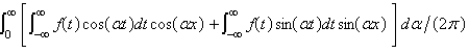
A)
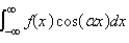
B)
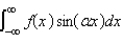
C)
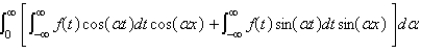
D)
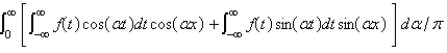
E)
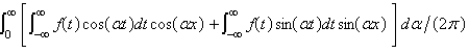

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
In the three previous problems, the solution for the temperature 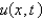 is
is
A)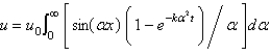
B)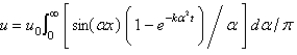
C)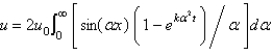
D)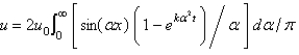
E)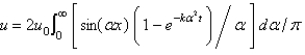
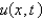 is
isA)
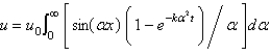
B)
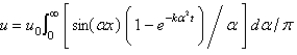
C)
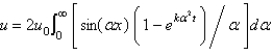
D)
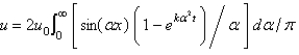
E)
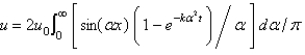

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
If 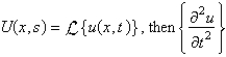 is
is
A)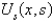
B)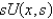
C)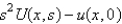
D)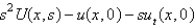
E)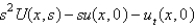
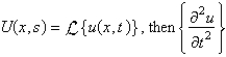 is
isA)
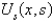
B)
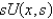
C)
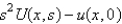
D)
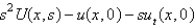
E)
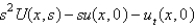

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
In the previous problem, apply the Laplace transform. The resulting equation for 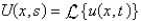 is
is
A)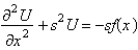
B)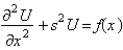
C)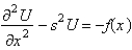
D)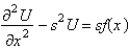
E)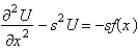
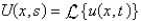 is
isA)
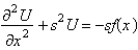
B)
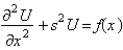
C)
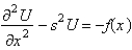
D)
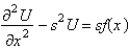
E)
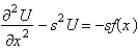

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
Suppose 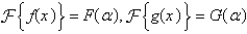 . In the convolution theorem, the formula for the Fourier transform is Select all that apply.
. In the convolution theorem, the formula for the Fourier transform is Select all that apply.
A)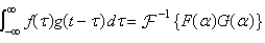
B)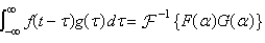
C)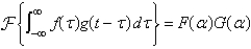
D)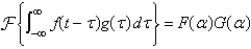
E) none of the above
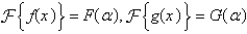 . In the convolution theorem, the formula for the Fourier transform is Select all that apply.
. In the convolution theorem, the formula for the Fourier transform is Select all that apply.A)
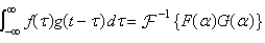
B)
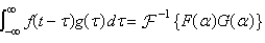
C)
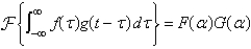
D)
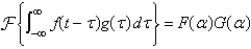
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
The complex form of the Fourier integral of a function f is
A)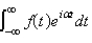
B)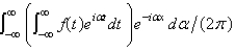
C)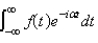
D)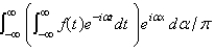
E)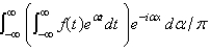
A)
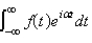
B)
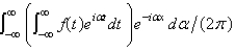
C)
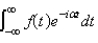
D)
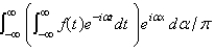
E)
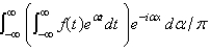

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
In the previous problem, the integral representation converges at 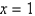 to the value
to the value
A) 0
B) 1
C)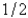
D) -1
E) none of the above
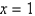 to the value
to the valueA) 0
B) 1
C)
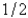
D) -1
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
In the three previous problems, the solution for 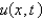 is
is
A)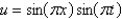
B)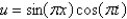
C)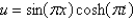
D)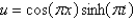
E)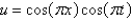
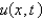 is
isA)
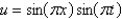
B)
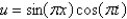
C)
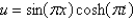
D)
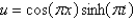
E)
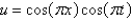

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
If 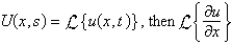 is
is
A)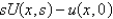
B)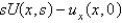
C)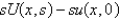
D)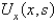
E)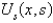
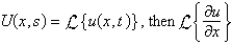 is
isA)
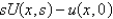
B)
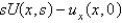
C)
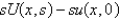
D)
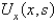
E)
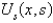

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
Let 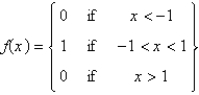 . The Fourier integral representation of f is
. The Fourier integral representation of f is 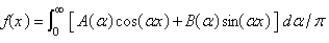 , where
, where
A)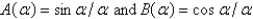
B)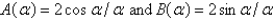
C)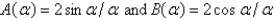
D)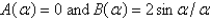
E)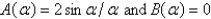
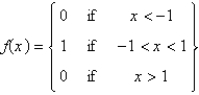 . The Fourier integral representation of f is
. The Fourier integral representation of f is 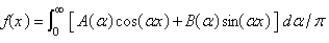 , where
, whereA)
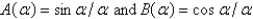
B)
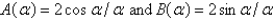
C)
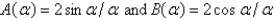
D)
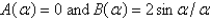
E)
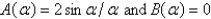

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the problem of a vibrating string, tightly-stretched between 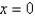 and
and 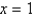 , with a fixed initial position,
, with a fixed initial position, 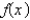 , and zero initial velocity. The mathematical problem for the deflection,
, and zero initial velocity. The mathematical problem for the deflection, 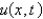 , is
, is 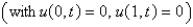
A)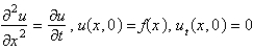
B)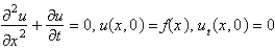
C)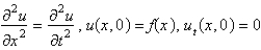
D)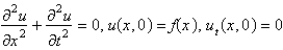
E)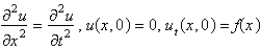
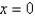 and
and 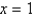 , with a fixed initial position,
, with a fixed initial position, 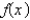 , and zero initial velocity. The mathematical problem for the deflection,
, and zero initial velocity. The mathematical problem for the deflection, 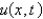 , is
, is 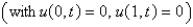
A)
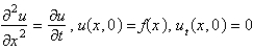
B)
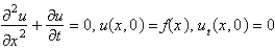
C)
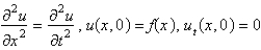
D)
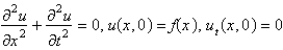
E)
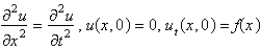

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
In the previous problem, apply a Fourier sine transform in x. The new problem for the transform 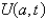 is
is
A)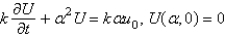
B)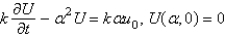
C)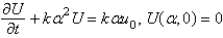
D)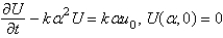
E)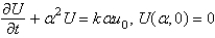
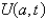 is
isA)
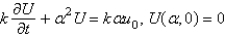
B)
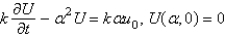
C)
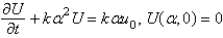
D)
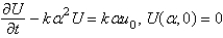
E)
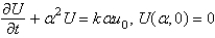

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
In the previous problem, the solution is
A)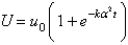
B)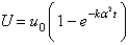
C)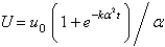
D)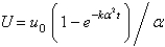
E)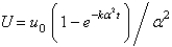
A)
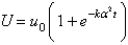
B)
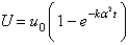
C)
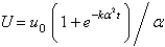
D)
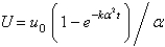
E)
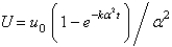

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


