Deck 15: Numerical Solutions of Partial Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 15: Numerical Solutions of Partial Differential Equations
1
In the previous two problems, let 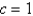 . Thesolutionforu along the line
. Thesolutionforu along the line 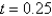 at the mesh points is Select all that apply.
at the mesh points is Select all that apply.
A)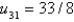
B)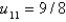
C)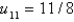
D)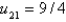
E)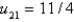
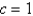 . Thesolutionforu along the line
. Thesolutionforu along the line 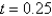 at the mesh points is Select all that apply.
at the mesh points is Select all that apply.A)
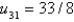
B)
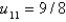
C)
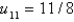
D)
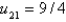
E)
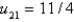
A, B, D
2
Laplace's equation is
A)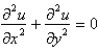
B)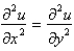
C)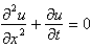
D)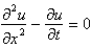
E)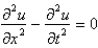
A)
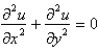
B)
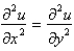
C)
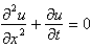
D)
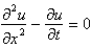
E)
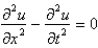
A
3
In the previous three problems, the values of 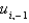 are
are
A)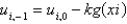
B)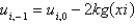
C)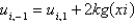
D)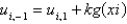
E)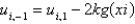
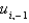 are
areA)
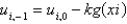
B)
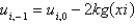
C)
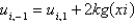
D)
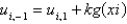
E)
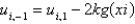
E
4
The heat equation is
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
In the previous problem, is the value of 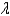 such that the scheme is stable?
such that the scheme is stable?
A) yes
B) no
C) It is right on the borderline.
D) It cannot be determined from the available data.
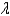 such that the scheme is stable?
such that the scheme is stable?A) yes
B) no
C) It is right on the borderline.
D) It cannot be determined from the available data.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
The five-point approximation of the Laplacian is
A)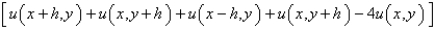
B)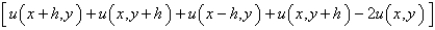
C)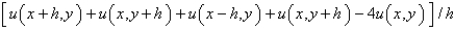
D)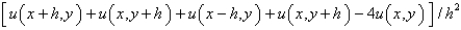
E)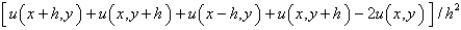
A)
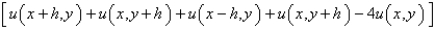
B)
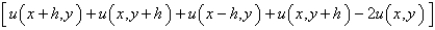
C)
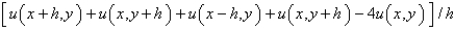
D)
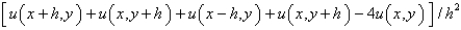
E)
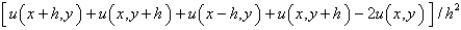

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the problem 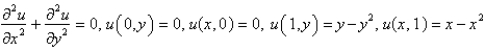 . A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of
. A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of 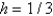 The conditions satisfied by the mesh points on the boundary are Select all that apply.
The conditions satisfied by the mesh points on the boundary are Select all that apply.
A)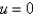 at (0, 1/3) and (1/3, 0)
at (0, 1/3) and (1/3, 0)
B)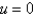 at (0, 2/3) and (2/3, 0)
at (0, 2/3) and (2/3, 0)
C)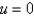 at (1/3, 1/3) and (2/3, 2/3)
at (1/3, 1/3) and (2/3, 2/3)
D)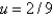 at (1, 1/3) and (1/3, 1)
at (1, 1/3) and (1/3, 1)
E)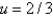 at (1, 2/3) and (2/3, 1)
at (1, 2/3) and (2/3, 1)
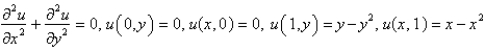 . A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of
. A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of 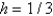 The conditions satisfied by the mesh points on the boundary are Select all that apply.
The conditions satisfied by the mesh points on the boundary are Select all that apply.A)
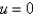 at (0, 1/3) and (1/3, 0)
at (0, 1/3) and (1/3, 0)B)
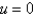 at (0, 2/3) and (2/3, 0)
at (0, 2/3) and (2/3, 0)C)
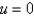 at (1/3, 1/3) and (2/3, 2/3)
at (1/3, 1/3) and (2/3, 2/3)D)
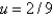 at (1, 1/3) and (1/3, 1)
at (1, 1/3) and (1/3, 1)E)
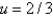 at (1, 2/3) and (2/3, 1)
at (1, 2/3) and (2/3, 1)
Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the problem 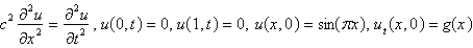 . Replace
. Replace 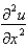 with a central difference approximation with
with a central difference approximation with 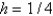 and
and 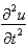 with a central difference approximation with
with a central difference approximation with 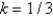 The resulting equation is
The resulting equation is
A)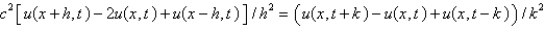
B)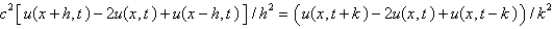
C)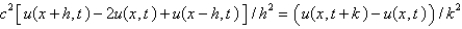
D)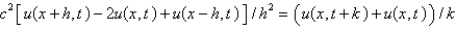
E)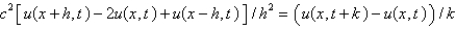
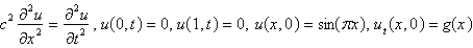 . Replace
. Replace 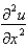 with a central difference approximation with
with a central difference approximation with 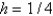 and
and 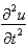 with a central difference approximation with
with a central difference approximation with 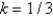 The resulting equation is
The resulting equation isA)
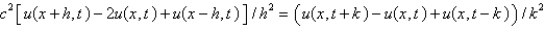
B)
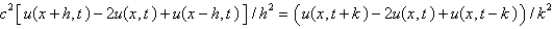
C)
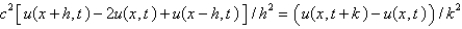
D)
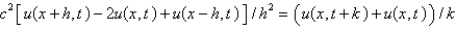
E)
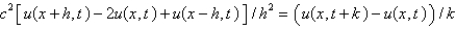

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
In the previous problem, using the notation 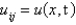 , and letting
, and letting 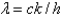 , the equation becomes
, the equation becomes
A)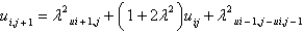
B)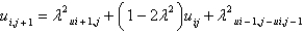
C)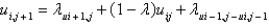
D)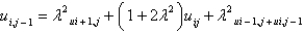
E)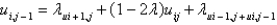
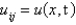 , and letting
, and letting 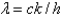 , the equation becomes
, the equation becomesA)
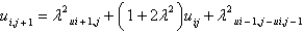
B)
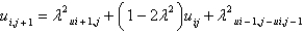
C)
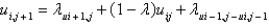
D)
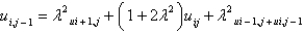
E)
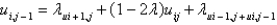

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
Laplace's equation is
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
The wave equation is
A)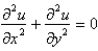
B)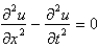
C)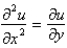
D)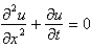
E)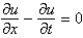
A)
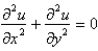
B)
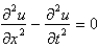
C)
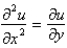
D)
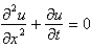
E)
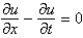

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
In the previous two problems, using 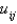 to denote the value of
to denote the value of 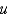 at the
at the 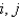 point, the equations for the values of the unknown function at the interior points are Select all that apply.
point, the equations for the values of the unknown function at the interior points are Select all that apply.
A)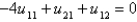
B)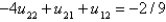
C)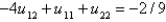
D)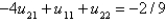
E)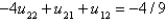
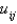 to denote the value of
to denote the value of 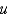 at the
at the 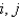 point, the equations for the values of the unknown function at the interior points are Select all that apply.
point, the equations for the values of the unknown function at the interior points are Select all that apply.A)
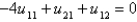
B)
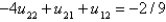
C)
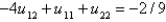
D)
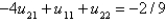
E)
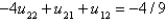

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
In the previous two problems, the values 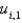 depend on the values
depend on the values 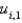 . How do you calculate those values?
. How do you calculate those values?
A) Use a central difference approximation in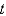 along the line
along the line 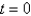 .
.
B) Use a forward difference approximation in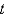 along the line
along the line 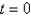 .
.
C) Use a backward difference approximation in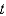 along the line
along the line 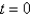 .
.
D) Use a forward difference approximation in x along the line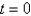 .
.
E) Use a backward difference approximation in x along the line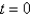 .
.
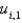 depend on the values
depend on the values 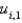 . How do you calculate those values?
. How do you calculate those values?A) Use a central difference approximation in
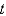 along the line
along the line 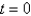 .
.B) Use a forward difference approximation in
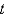 along the line
along the line 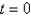 .
.C) Use a backward difference approximation in
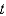 along the line
along the line 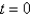 .
.D) Use a forward difference approximation in x along the line
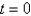 .
.E) Use a backward difference approximation in x along the line
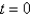 .
.
Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
In the previous problem, using the notation 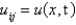 , and letting
, and letting 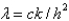 , the equation becomes
, the equation becomes
A)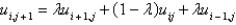
B)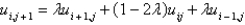
C)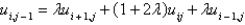
D)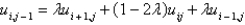
E)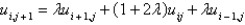
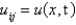 , and letting
, and letting 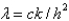 , the equation becomes
, the equation becomesA)
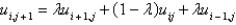
B)
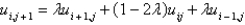
C)
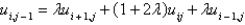
D)
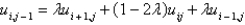
E)
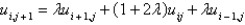

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
The central difference approximation for 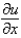 with step size
with step size 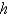 is
is
A)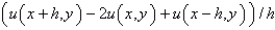
B)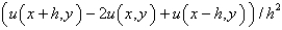
C)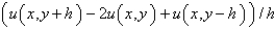
D)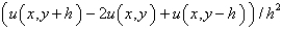
E)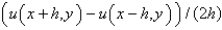
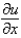 with step size
with step size 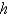 is
isA)
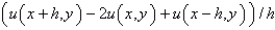
B)
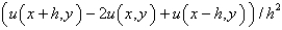
C)
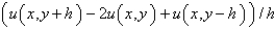
D)
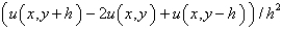
E)
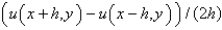

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
A Dirichlet problem is a partial differential equation with conditions specifying
A) a linear combination of the values of the unknown function along the boundary and the values of the derivative of the unknown function along the boundary
B) the values of the unknown function along the boundary
C) the values of the derivative of the unknown function along the boundary
D) none of the above
A) a linear combination of the values of the unknown function along the boundary and the values of the derivative of the unknown function along the boundary
B) the values of the unknown function along the boundary
C) the values of the derivative of the unknown function along the boundary
D) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
In the four previous problems, let 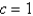 . The calculated values of
. The calculated values of 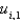 are Select all that apply.
are Select all that apply.
A)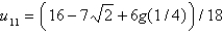
B)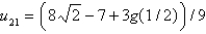
C)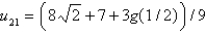
D)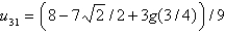
E)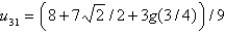
 . The calculated values of
. The calculated values of  are Select all that apply.
are Select all that apply.A)
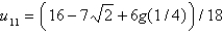
B)
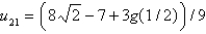
C)
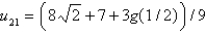
D)
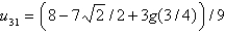
E)
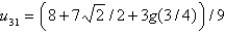

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
In the previous five problems, is the value of 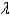 such that the numerical scheme is stable?
such that the numerical scheme is stable?
A) yes
B) no
C) It is in the borderline.
D) It cannot be determined from the available data.
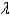 such that the numerical scheme is stable?
such that the numerical scheme is stable?A) yes
B) no
C) It is in the borderline.
D) It cannot be determined from the available data.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
In the previous three problems, the solution at the interior points is Select all that apply.
A)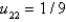
B)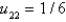
C)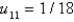
D)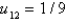
E)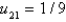
A)
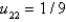
B)
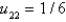
C)
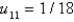
D)
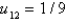
E)
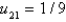

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
The central difference approximation for 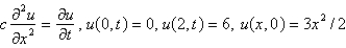 Replace
Replace 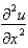 with a central difference approximation with
with a central difference approximation with 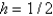 and
and 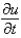 with a forward difference approximation with
with a forward difference approximation with 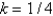 . The resulting equation is
. The resulting equation is
A)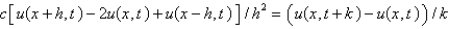
B)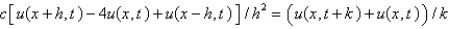
C)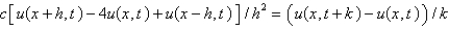
D)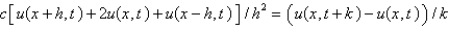
E)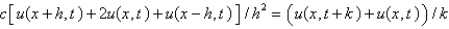
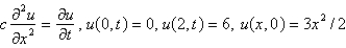 Replace
Replace 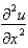 with a central difference approximation with
with a central difference approximation with 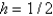 and
and 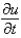 with a forward difference approximation with
with a forward difference approximation with 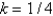 . The resulting equation is
. The resulting equation isA)
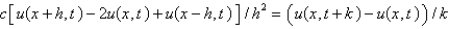
B)
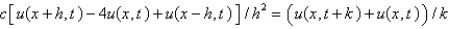
C)
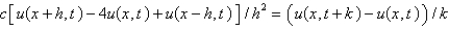
D)
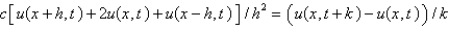
E)
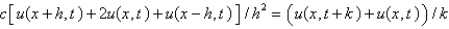

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
The heat equation is
A)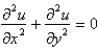
B)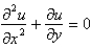
C)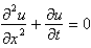
D)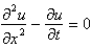
E)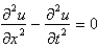
A)
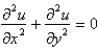
B)
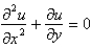
C)
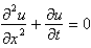
D)
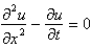
E)
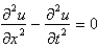

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
The central difference approximation for 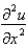 with step size
with step size 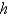 is
is
A)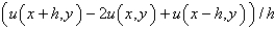
B)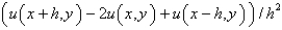
C)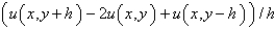
D)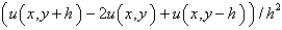
E)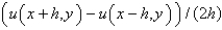
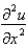 with step size
with step size 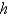 is
isA)
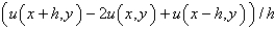
B)
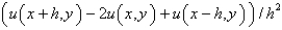
C)
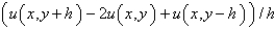
D)
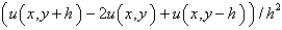
E)
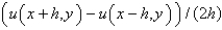

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The wave equation is
A)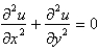
B)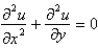
C)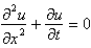
D)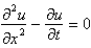
E)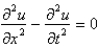
A)
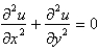
B)
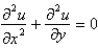
C)
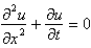
D)
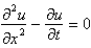
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
In the four previous problems, let 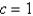 . The calculated values of
. The calculated values of 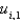 are
are
A)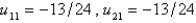
B)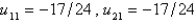
C)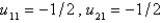
D)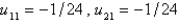
E)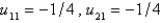
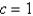 . The calculated values of
. The calculated values of 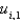 are
areA)
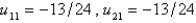
B)
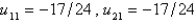
C)
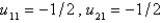
D)
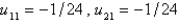
E)
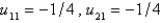

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
In the previous two problems, the values 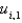 depend on the values
depend on the values 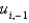 . How do you calculate those values?
. How do you calculate those values?
A) Use a forward difference approximation in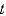 along the line
along the line 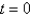 .
.
B) Use a backward difference approximation in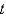 along the line
along the line 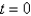 .
.
C) Use a central difference approximation in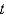 along the line
along the line 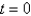 .
.
D) Use a forward difference approximation in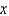 along the line
along the line 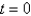 .
.
E) Use a backward difference approximation in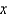 along the line
along the line 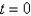 .
.
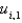 depend on the values
depend on the values 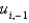 . How do you calculate those values?
. How do you calculate those values?A) Use a forward difference approximation in
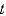 along the line
along the line 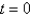 .
.B) Use a backward difference approximation in
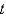 along the line
along the line 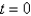 .
.C) Use a central difference approximation in
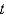 along the line
along the line 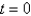 .
.D) Use a forward difference approximation in
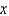 along the line
along the line 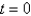 .
.E) Use a backward difference approximation in
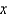 along the line
along the line 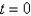 .
.
Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
The forward difference approximation of 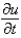 with step size k is
with step size k is
A)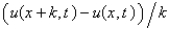
B)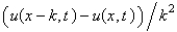
C)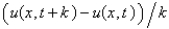
D)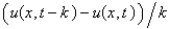
E)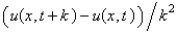
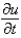 with step size k is
with step size k isA)
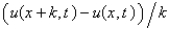
B)
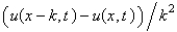
C)
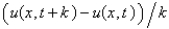
D)
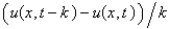
E)
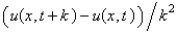

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
In the previous three problems, the solution at the interior points is Select all that apply.
A)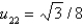
B)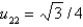
C)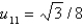
D)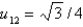
E)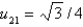
A)
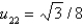
B)
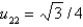
C)
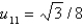
D)
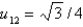
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
In the previous problem, using the notation 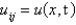 , and letting
, and letting 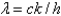 , the equation becomes
, the equation becomes
A)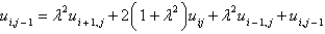
B)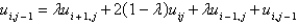
C)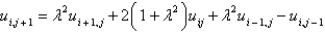
D)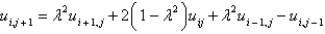
E)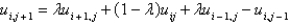
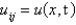 , and letting
, and letting 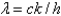 , the equation becomes
, the equation becomesA)
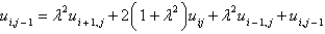
B)
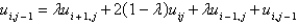
C)
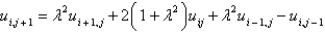
D)
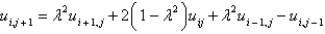
E)
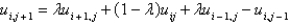

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
In the previous problem, using the notation 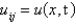 , and letting
, and letting 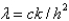 , the equation becomes
, the equation becomes
A)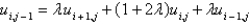
B)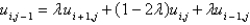
C)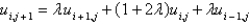
D)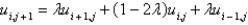
E)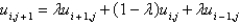
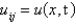 , and letting
, and letting 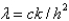 , the equation becomes
, the equation becomesA)
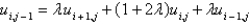
B)
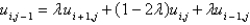
C)
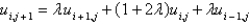
D)
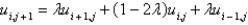
E)
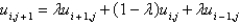

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
The wave equation is
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
In the previous three problems, if 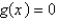 then the values of
then the values of 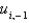 are
are
A)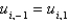
B)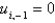
C)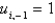
D)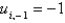
E) none of the above
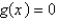 then the values of
then the values of 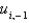 are
areA)
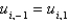
B)
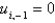
C)
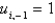
D)
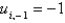
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
Consider the problem 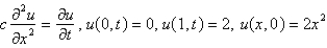 . Replace
. Replace 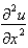 with a central difference approximation with
with a central difference approximation with 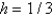 and
and 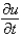 with a forward difference approximation with
with a forward difference approximation with 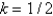 . The resulting equation is
. The resulting equation is
A)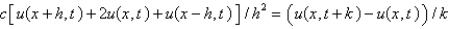
B)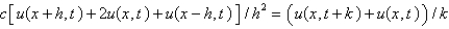
C)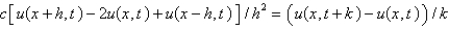
D)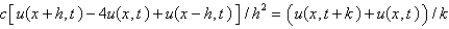
E)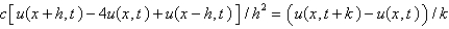
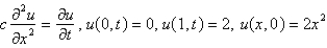 . Replace
. Replace 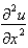 with a central difference approximation with
with a central difference approximation with 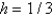 and
and 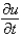 with a forward difference approximation with
with a forward difference approximation with 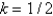 . The resulting equation is
. The resulting equation isA)
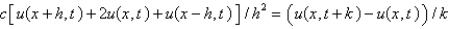
B)
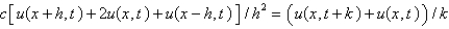
C)
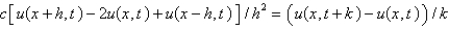
D)
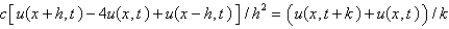
E)
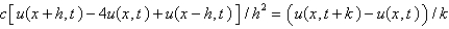

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the problem 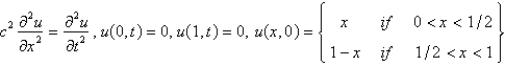 ,
, 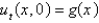 . Replace
. Replace 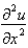 with a central difference approximation with
with a central difference approximation with 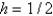 and
and 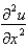 with a central difference approximation with
with a central difference approximation with 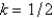 . The resulting equation is
. The resulting equation is
A)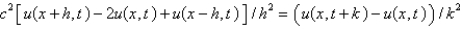
B)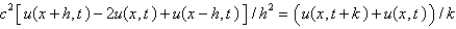
C)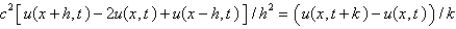
D)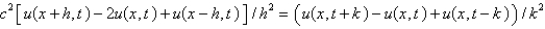
E)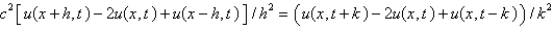
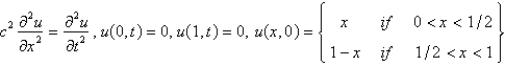 ,
, 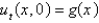 . Replace
. Replace 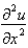 with a central difference approximation with
with a central difference approximation with 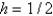 and
and 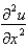 with a central difference approximation with
with a central difference approximation with 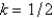 . The resulting equation is
. The resulting equation isA)
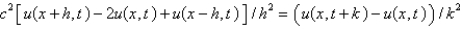
B)
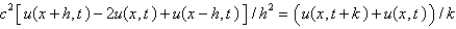
C)
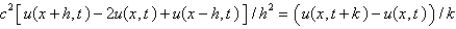
D)
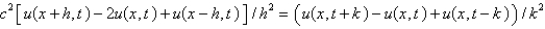
E)
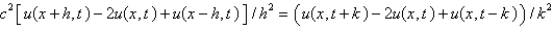

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
In the previous two problems, let 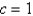 . Thesolution for u along the line
. Thesolution for u along the line 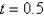 at the mesh points is Select all that apply.
at the mesh points is Select all that apply.
A)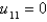
B)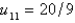
C)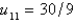
D)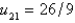
E)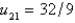
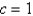 . Thesolution for u along the line
. Thesolution for u along the line 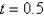 at the mesh points is Select all that apply.
at the mesh points is Select all that apply.A)
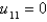
B)
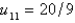
C)
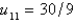
D)
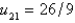
E)
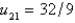

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
A Dirichlet problem is a partial differential equation with conditions specifying
A) the values of the unknown function along the boundary
B) the values of the derivative of the unknown function along the boundary
C) a linear combination of the values of the unknown function along the boundary and the values of the derivative of the unknown function along the boundary
D) none of the above
A) the values of the unknown function along the boundary
B) the values of the derivative of the unknown function along the boundary
C) a linear combination of the values of the unknown function along the boundary and the values of the derivative of the unknown function along the boundary
D) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
Laplace's equation is
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above
A) hyperbolic
B) parabolic
C) elliptic
D) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
In the previous problem, is the value of 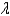 such that the scheme is stable?
such that the scheme is stable?
A) yes
B) no
C) It is right on the borderline.
D) It cannot be determined from the available data.
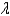 such that the scheme is stable?
such that the scheme is stable?A) yes
B) no
C) It is right on the borderline.
D) It cannot be determined from the available data.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
In the previous two problems, using 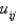 to denote the value of
to denote the value of 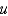 at the
at the 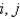 point, the equations for the values of the unknown function at the interior points are Select all that apply.
point, the equations for the values of the unknown function at the interior points are Select all that apply.
A)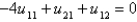
B)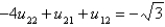
C)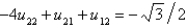
D)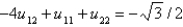
E)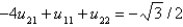
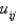 to denote the value of
to denote the value of 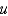 at the
at the 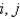 point, the equations for the values of the unknown function at the interior points are Select all that apply.
point, the equations for the values of the unknown function at the interior points are Select all that apply.A)
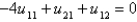
B)
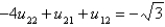
C)
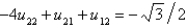
D)
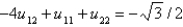
E)
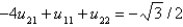

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
The five point approximation of the Laplacian is
A)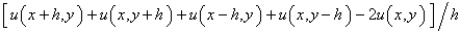
B)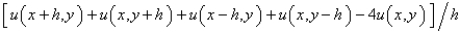
C)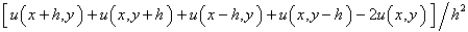
D)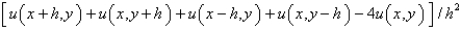
E)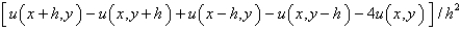
A)
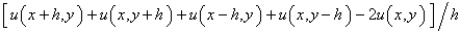
B)
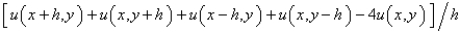
C)
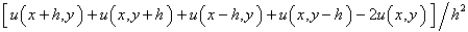
D)
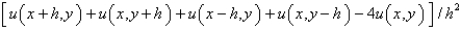
E)
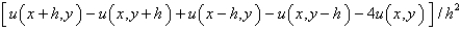

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
Consider the problem 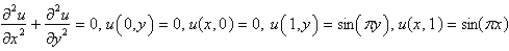 . A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of
. A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of 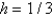 The conditions satisfied by the mesh points on the boundary are Select all that apply.
The conditions satisfied by the mesh points on the boundary are Select all that apply.
A)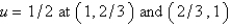
B)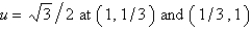
C)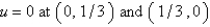
D)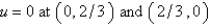
E)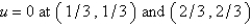
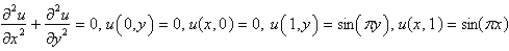 . A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of
. A finite difference approximation of the solution is desired, using the approximation of the previous problem. Use a mesh size of 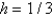 The conditions satisfied by the mesh points on the boundary are Select all that apply.
The conditions satisfied by the mesh points on the boundary are Select all that apply.A)
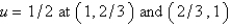
B)
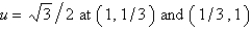
C)
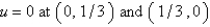
D)
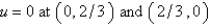
E)
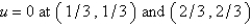

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


