Deck 11: Orthogonal Functions and Fourier Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 11: Orthogonal Functions and Fourier Series
1
The solution of the eigenvalue problem 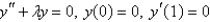 is
is
A)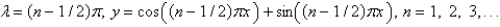
B)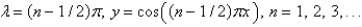
C)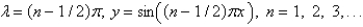
D)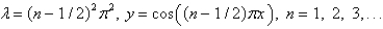
E)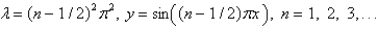
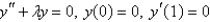 is
isA)
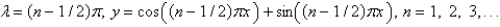
B)
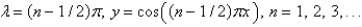
C)
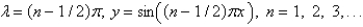
D)
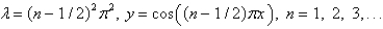
E)
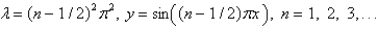
E
2
In order to be assured by a theorem that the Fourier Series of 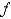 on
on 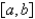 converges at
converges at 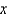 , to
, to 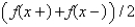 which of the following conditions need to be satisfied? Select all that apply.
which of the following conditions need to be satisfied? Select all that apply.
A)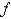 is continuous on
is continuous on 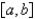
B)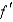 is continuous on
is continuous on 
C)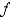 is piecewise continuous on
is piecewise continuous on 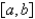
D)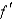 is piecewise continuous on
is piecewise continuous on 
E) is integrable on
is integrable on 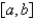
 on
on 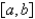 converges at
converges at 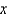 , to
, to 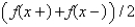 which of the following conditions need to be satisfied? Select all that apply.
which of the following conditions need to be satisfied? Select all that apply.A)
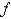 is continuous on
is continuous on 
B)
 is continuous on
is continuous on 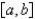
C)
 is piecewise continuous on
is piecewise continuous on 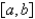
D)
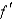 is piecewise continuous on
is piecewise continuous on 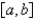
E)
 is integrable on
is integrable on 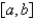
C, D, E
3
The problem 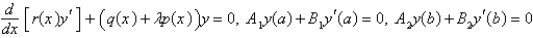 is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.
is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.
A)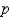 ,
, 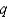 ,
, 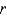 piecewise continuous on
piecewise continuous on 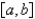
B)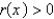 and
and 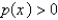 on
on 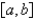
C)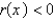 and
and 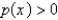 on
on 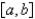
D)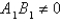
E)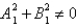
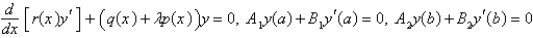 is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.
is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.A)
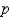 ,
, 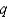 ,
, 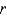 piecewise continuous on
piecewise continuous on 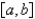
B)
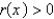 and
and 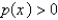 on
on 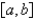
C)
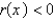 and
and 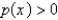 on
on 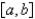
D)
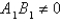
E)
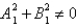
B, E
4
The square norm of the function 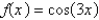 on the interval
on the interval 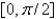 is
is
A) 1
B)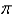
C)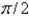
D)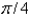
E) 0
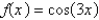 on the interval
on the interval 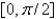 is
isA) 1
B)
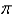
C)
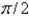
D)
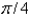
E) 0

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
The Fourier series of an even function might Select all that apply.
A) contain sine terms
B) contain cosine terms
C) contain a constant term
D) contain sine and cosine terms
E) contain sine, cosine, and constant terms
A) contain sine terms
B) contain cosine terms
C) contain a constant term
D) contain sine and cosine terms
E) contain sine, cosine, and constant terms

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
The square norm of the function 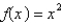 on the interval
on the interval 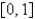 is
is
A) 1/2
B) 1/3
C) 1/5
D) 1
E) 0
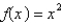 on the interval
on the interval 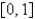 is
isA) 1/2
B) 1/3
C) 1/5
D) 1
E) 0

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
The differential equation 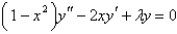 is
is
A) Legendre's equation
B) Bessel's equation
C) the Fourier-Bessel
D) the hypergeometric
E) none of the above
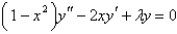 is
isA) Legendre's equation
B) Bessel's equation
C) the Fourier-Bessel
D) the hypergeometric
E) none of the above

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8
The Fourier series of the function 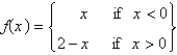 on
on 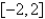 are Select all that apply.
are Select all that apply.
A) contains only cosine terms
B) contains only sine terms
C) contains sine and cosine terms
D) contains a constant term
E) contains sine, cosine, and constant terms
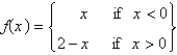 on
on 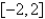 are Select all that apply.
are Select all that apply.A) contains only cosine terms
B) contains only sine terms
C) contains sine and cosine terms
D) contains a constant term
E) contains sine, cosine, and constant terms

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
The solution of the eigenvalue problem 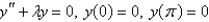 is
is
A)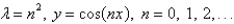
B)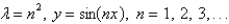
C)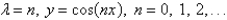
D)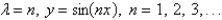
E)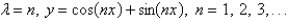
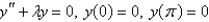 is
isA)
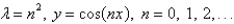
B)
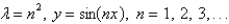
C)
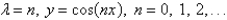
D)
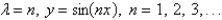
E)
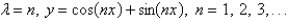

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
The Fourier coeficients of the function 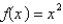 on
on 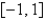 are Select all that apply.
are Select all that apply.
A)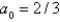
B)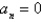
C)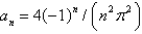
D)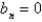
E)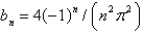
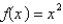 on
on 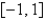 are Select all that apply.
are Select all that apply.A)
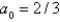
B)
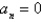
C)
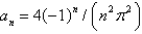
D)
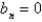
E)
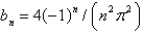

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
The problem 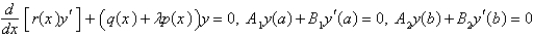 is not a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.
is not a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.
A)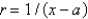 on
on 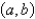
B)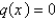 on
on 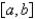
C)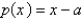 on
on 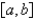
D)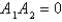
E)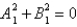
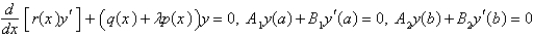 is not a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.
is not a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.A)
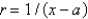 on
on 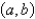
B)
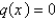 on
on 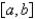
C)
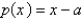 on
on 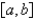
D)
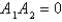
E)
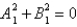

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
The solution of the eigenvalue problem 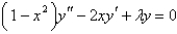 where
where 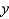 is bounded on
is bounded on 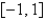 , is
, is
A)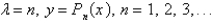
B)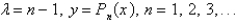
C)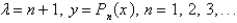
D)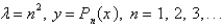
E)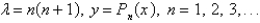
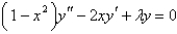 where
where 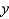 is bounded on
is bounded on 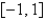 , is
, isA)
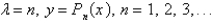
B)
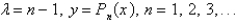
C)
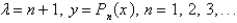
D)
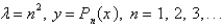
E)
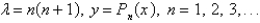

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following differential equations are in self-adjoint form? Select all that apply.
A)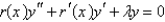
B)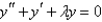
C)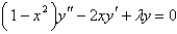
D)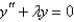
E)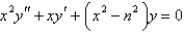
A)
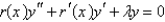
B)
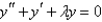
C)
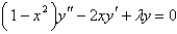
D)
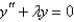
E)
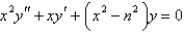

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
The Fourier Series of a function 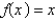 defined on
defined on 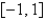 is
is 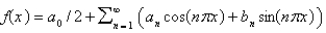 where Select all that apply.
where Select all that apply.
A)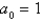
B)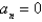
C)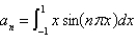
D)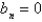
E)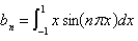
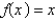 defined on
defined on 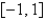 is
is 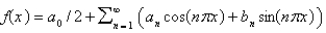 where Select all that apply.
where Select all that apply.A)
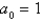
B)
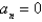
C)
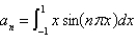
D)
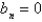
E)
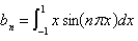

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
The function 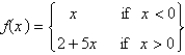 has a Fourier series on
has a Fourier series on 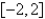 that converges at
that converges at 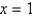 to
to
A) 7
B) 1
C) 1/2
D)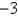
E) unknown
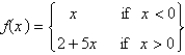 has a Fourier series on
has a Fourier series on 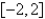 that converges at
that converges at 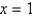 to
toA) 7
B) 1
C) 1/2
D)
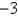
E) unknown

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
Using the eigenfunctions of the previous problem, the Fourier-Legendre series for the function 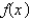 is
is 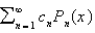 , where
, where
A)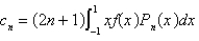
B)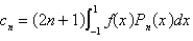
C)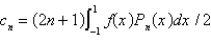
D)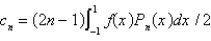
E)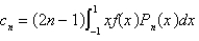
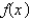 is
is 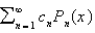 , where
, whereA)
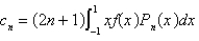
B)
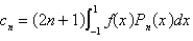
C)
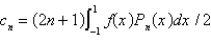
D)
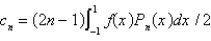
E)
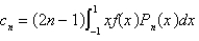

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
The function 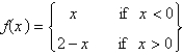 is Select all that apply.
is Select all that apply.
A) odd
B) even
C) neither even nor odd
D) continuous on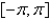
E) discontinuous on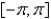
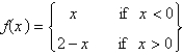 is Select all that apply.
is Select all that apply.A) odd
B) even
C) neither even nor odd
D) continuous on
E) discontinuous on

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
An example of a regular Sturm-Liouville problem is 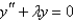 with boundary conditions Select all that apply.
with boundary conditions Select all that apply.
A)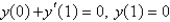
B)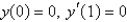
C)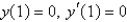
D)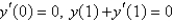
E)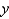 is bounded on
is bounded on 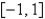
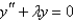 with boundary conditions Select all that apply.
with boundary conditions Select all that apply.A)
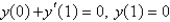
B)
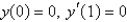
C)
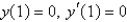
D)
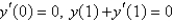
E)
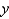 is bounded on
is bounded on 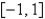

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
The function 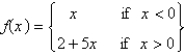 has a Fourier series on
has a Fourier series on 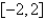 that converges at
that converges at 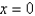 to
to
A) 0
B) 1
C) 1/2
D) 2
E) unknown
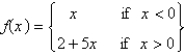 has a Fourier series on
has a Fourier series on 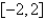 that converges at
that converges at 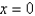 to
toA) 0
B) 1
C) 1/2
D) 2
E) unknown

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
The Fourier series of the function 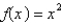 on
on 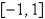 is
is
A)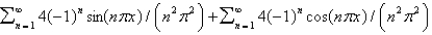
B)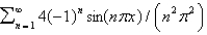
C)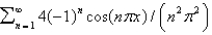
D)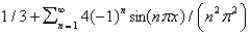
E)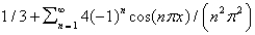
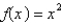 on
on 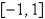 is
isA)
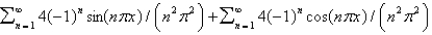
B)
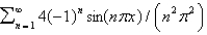
C)
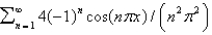
D)
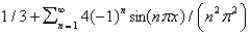
E)
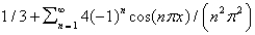

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
The Fourier Series of a function 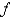 defined on
defined on 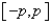 is
is 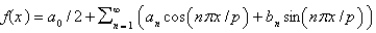 where Select all that apply.
where Select all that apply.
A)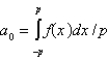
B)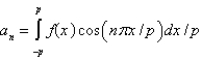
C)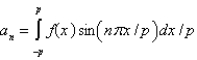
D)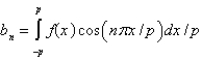
E)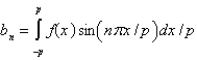
 defined on
defined on  is
is 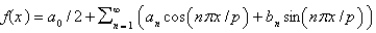 where Select all that apply.
where Select all that apply.A)
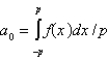
B)
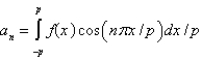
C)
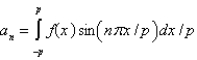
D)
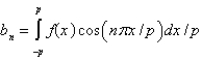
E)
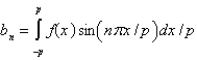

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
Using the eigenfunctions of the previous problem, written as 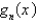 , the Fourier-Bessel series for the function
, the Fourier-Bessel series for the function  is
is 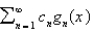 , where
, where
A)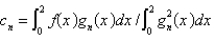
B)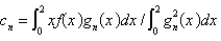
C)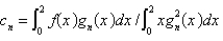
D)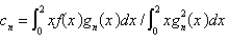
E)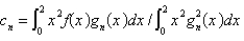
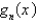 , the Fourier-Bessel series for the function
, the Fourier-Bessel series for the function  is
is 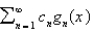 , where
, whereA)
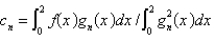
B)
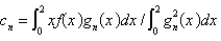
C)
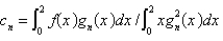
D)
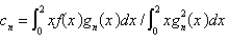
E)
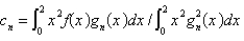

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The solution of the eigenvalue problem 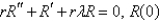 is bounded,
is bounded, 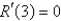 is
is 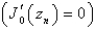
A)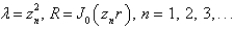
B)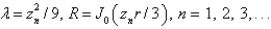
C)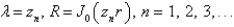
D)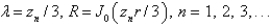
E)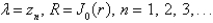
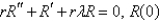 is bounded,
is bounded, 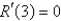 is
is 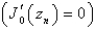
A)
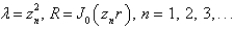
B)
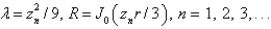
C)
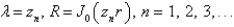
D)
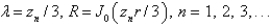
E)
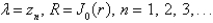

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
The square norm of the function 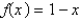 on the interval
on the interval 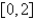 is
is
A) 2/3
B)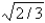
C) 1/3
D)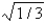
E) 0
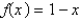 on the interval
on the interval 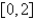 is
isA) 2/3
B)
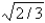
C) 1/3
D)
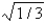
E) 0

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
The solution of the eigenvalue problem 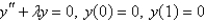 is
is
A)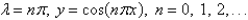
B)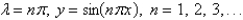
C)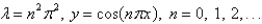
D)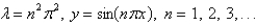
E)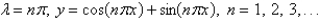
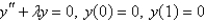 is
isA)
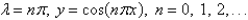
B)
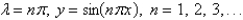
C)
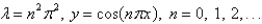
D)
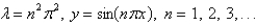
E)
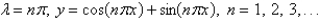

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the differential equation 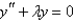 . Examples of boundary conditions for this equation that make a regular Sturm-Liouville problem are Select all that apply.
. Examples of boundary conditions for this equation that make a regular Sturm-Liouville problem are Select all that apply.
A)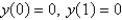
B)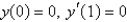
C)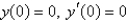
D)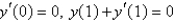
E)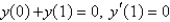
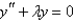 . Examples of boundary conditions for this equation that make a regular Sturm-Liouville problem are Select all that apply.
. Examples of boundary conditions for this equation that make a regular Sturm-Liouville problem are Select all that apply.A)
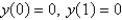
B)
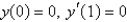
C)
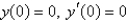
D)
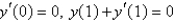
E)
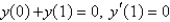

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
The Fourier series of the function 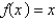 on
on 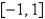 is
is
A)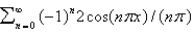
B)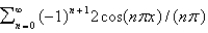
C)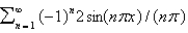
D)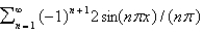
E)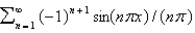
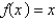 on
on 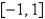 is
isA)
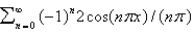
B)
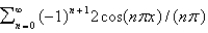
C)
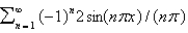
D)
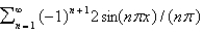
E)
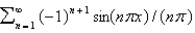

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
The square norm of the function 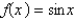 on the interval
on the interval 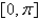 is
is
A) 1
B)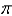
C)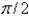
D)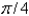
E) 0
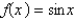 on the interval
on the interval 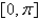 is
isA) 1
B)
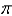
C)
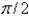
D)
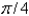
E) 0

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
In order to be assured by a theorem that the Fourier Series of  on
on 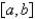 converges to
converges to 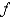 , which of the following conditions need to be satisfied? Select all that apply.
, which of the following conditions need to be satisfied? Select all that apply.
A)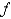 is continuous on
is continuous on 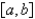
B) is continuous on
is continuous on 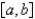
C) is piecewise continuous on
is piecewise continuous on 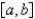
D) is piecewise continuous on
is piecewise continuous on 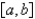
E) is integrable on
is integrable on 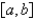
 on
on 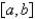 converges to
converges to  , which of the following conditions need to be satisfied? Select all that apply.
, which of the following conditions need to be satisfied? Select all that apply.A)
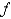 is continuous on
is continuous on 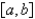
B)
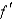 is continuous on
is continuous on 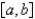
C)
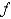 is piecewise continuous on
is piecewise continuous on 
D)
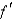 is piecewise continuous on
is piecewise continuous on 
E)
 is integrable on
is integrable on 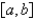

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
The function 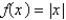 is Select all that apply.
is Select all that apply.
A) odd
B) even
C) neither even nor odd
D) continuous on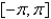
E) discontinuous on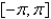
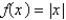 is Select all that apply.
is Select all that apply.A) odd
B) even
C) neither even nor odd
D) continuous on
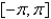
E) discontinuous on
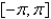

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
The problem 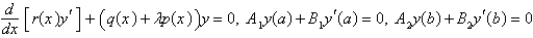 is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.
is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.
A)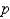 ,
, 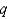 ,
, 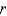 are continuous on
are continuous on 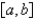
B)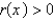 and
and 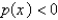 on
on 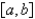
C)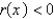 and
and 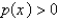 on
on 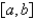
D)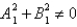
E)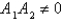
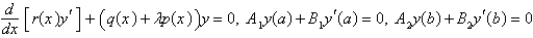 is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.
is a regular Sturm-Liouville problem under certain conditions, including Select all that apply.A)
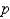 ,
, 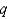 ,
, 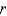 are continuous on
are continuous on 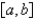
B)
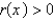 and
and 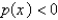 on
on 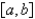
C)
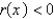 and
and 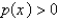 on
on 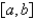
D)
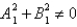
E)
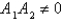

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
The solution of the eigenvalue problem 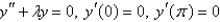 is
is
A)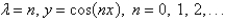
B)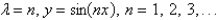
C)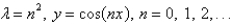
D)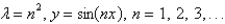
E)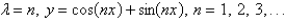
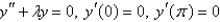 is
isA)
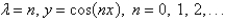
B)
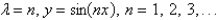
C)
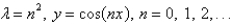
D)
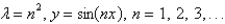
E)
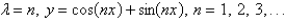

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following differential equations are in self-adjoint form? Select all that apply.
A)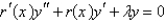
B)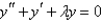
C)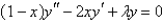
D)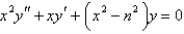
E)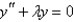
A)
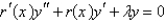
B)
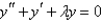
C)
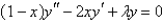
D)
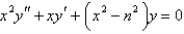
E)
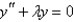

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
The problem 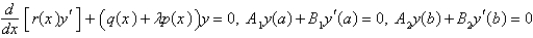 is a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.
is a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.
A)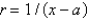 are continuous on
are continuous on 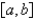
B)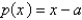 on
on 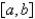
C)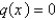 on
on 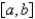
D)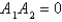
E)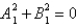
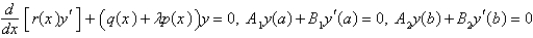 is a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.
is a regular Sturm-Liouville problem under which of the following conditions. Select all that apply.A)
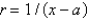 are continuous on
are continuous on 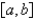
B)
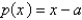 on
on 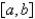
C)
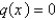 on
on 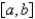
D)
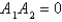
E)
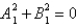

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
The function 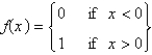 has a Fourier series on
has a Fourier series on 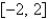 that converges at
that converges at 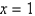 to
to
A) 0
B) 1
C) 1/2
D)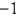
E) unknown
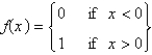 has a Fourier series on
has a Fourier series on 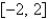 that converges at
that converges at 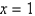 to
toA) 0
B) 1
C) 1/2
D)
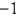
E) unknown

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
The Fourier series of an odd function might Select all that apply.
A) contain sine terms
B) contain cosine terms
C) contain a constant term
D) contain sine and cosine terms
E) contain sine, cosine, and constant terms
A) contain sine terms
B) contain cosine terms
C) contain a constant term
D) contain sine and cosine terms
E) contain sine, cosine, and constant terms

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
The Fourier series of the function 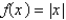 on
on 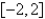 is Select all that apply.
is Select all that apply.
A) contains cosine terms
B) contains sine terms
C) contains sine and cosine terms
D) contains a constant term
E) contains sine, cosine, and constant terms
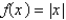 on
on 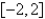 is Select all that apply.
is Select all that apply.A) contains cosine terms
B) contains sine terms
C) contains sine and cosine terms
D) contains a constant term
E) contains sine, cosine, and constant terms

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
The function 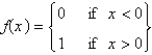 has a Fourier series on
has a Fourier series on 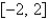 that converges at
that converges at 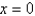 to
to
A) 0
B) 1
C) 1/2
D)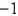
E) unknown
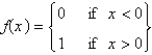 has a Fourier series on
has a Fourier series on 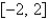 that converges at
that converges at 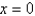 to
toA) 0
B) 1
C) 1/2
D)
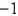
E) unknown

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the parameterized Bessel's differential equation 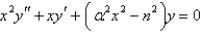 along with the conditions
along with the conditions 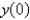 is bounded,
is bounded, 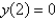 . The solution of this eigenvalue problem is
. The solution of this eigenvalue problem is 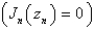
A)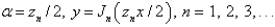
B)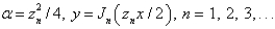
C)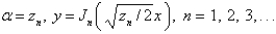
D)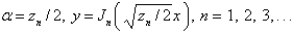
E)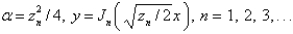
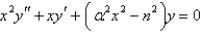 along with the conditions
along with the conditions 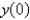 is bounded,
is bounded, 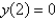 . The solution of this eigenvalue problem is
. The solution of this eigenvalue problem is 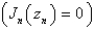
A)
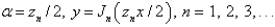
B)
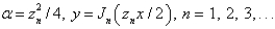
C)
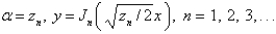
D)
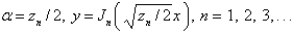
E)
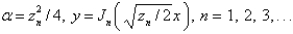

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
The Fourier coeficients of the function 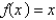 on
on 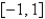 are
are
A)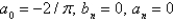
B)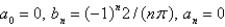
C)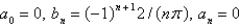
D)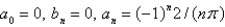
E)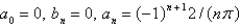
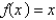 on
on 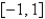 are
areA)
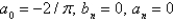
B)
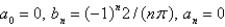
C)
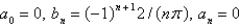
D)
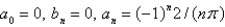
E)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


