Deck 8: Further Applications of Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/87
Play
Full screen (f)
Deck 8: Further Applications of Integration
1
A movie theater has been charging $ 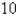 .00 per person and selling about
.00 per person and selling about 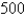 tickets on a typical weeknight. After surveying their customers, the theater estimates that for every $
tickets on a typical weeknight. After surveying their customers, the theater estimates that for every $ 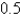 that they lower the price, the number of moviegoers will increase by
that they lower the price, the number of moviegoers will increase by 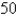 per night. Find the demand function and calculate the consumer surplus when the tickets are priced at $
per night. Find the demand function and calculate the consumer surplus when the tickets are priced at $ 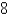 .
.
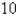 .00 per person and selling about
.00 per person and selling about 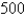 tickets on a typical weeknight. After surveying their customers, the theater estimates that for every $
tickets on a typical weeknight. After surveying their customers, the theater estimates that for every $ 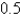 that they lower the price, the number of moviegoers will increase by
that they lower the price, the number of moviegoers will increase by 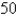 per night. Find the demand function and calculate the consumer surplus when the tickets are priced at $
per night. Find the demand function and calculate the consumer surplus when the tickets are priced at $ 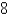 .
.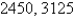
2
The manager of a fast-food restaurant determines that the average time that her customers wait for service is 2 minutes. Find the probability that a customer is served within the first 2 minutes.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
The manager of a fast-food restaurant determines that the average time that her customers wait for service is 2 minutes.
The manager wants to advertise that anybody who isn't served within a certain number of minutes gets a free hamburger. But she doesn't want to give away free hamburgers to more than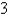 % of her customers. What value of x must she use in the advertisement "if you aren't served within x minutes, you get a free hamburger"?
% of her customers. What value of x must she use in the advertisement "if you aren't served within x minutes, you get a free hamburger"?
The manager wants to advertise that anybody who isn't served within a certain number of minutes gets a free hamburger. But she doesn't want to give away free hamburgers to more than
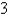 % of her customers. What value of x must she use in the advertisement "if you aren't served within x minutes, you get a free hamburger"?
% of her customers. What value of x must she use in the advertisement "if you aren't served within x minutes, you get a free hamburger"?
4
A type of lightbulb is labeled as having an average lifetime of 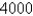 hours. It's reasonable to model the probability of failure of these bulbs by an exponential density function with mean µ =
hours. It's reasonable to model the probability of failure of these bulbs by an exponential density function with mean µ = 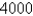 . What is the median lifetime of these lightbulbs? Give your answer rounded to two decimal places.
. What is the median lifetime of these lightbulbs? Give your answer rounded to two decimal places.
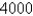 hours. It's reasonable to model the probability of failure of these bulbs by an exponential density function with mean µ =
hours. It's reasonable to model the probability of failure of these bulbs by an exponential density function with mean µ = 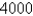 . What is the median lifetime of these lightbulbs? Give your answer rounded to two decimal places.
. What is the median lifetime of these lightbulbs? Give your answer rounded to two decimal places.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
5
A hot, wet summer is causing a mosquito population explosion in a lake resort area. The number of mosquitoes is increasing at an estimated rate of per week (where t is measured in weeks). By how much does the mosquito population increase between the 4th and 6 th weeks of summer?
A)
B) 7702
C) 5702
D) 6702
E) 8702
A)
B) 7702
C) 5702
D) 6702
E) 8702

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
6
If f (x) is the probability density function for the blood cholesterol level of men over the age of 40, where x is measured in milligrams per deciliter, express as an integral the probability that the cholesterol level of such a man lies between 195 and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
7
Let 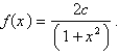 a) For what value of c is f a probability density function?
a) For what value of c is f a probability density function?
b) For that value of c, find P (-1 < X < 1).
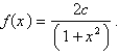 a) For what value of c is f a probability density function?
a) For what value of c is f a probability density function?b) For that value of c, find P (-1 < X < 1).

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
8
Let the function whose graph is shown be a probability density function. Calculate the mean. 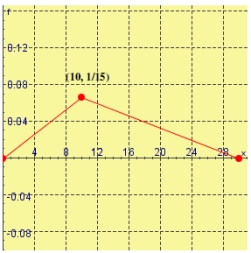


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
9
A demand curve is given by 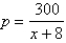 .
.
Find the consumer surplus when the selling price is $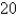 .
.
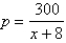 .
.Find the consumer surplus when the selling price is $
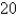 .
.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
10
A gate in an irrigation canal is constructed in the form of a trapezoid ft wide at the bottom, ft wide at the top, and 2 ft high. It is placed vertically in the canal, with the water extending to its top. Find the hydrostatic force on one side of the gate..
A) lb
B) lb
C) lb
D) lb
E) None of these
A) lb
B) lb
C) lb
D) lb
E) None of these

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
11
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 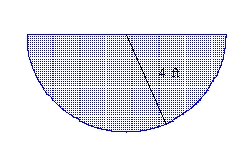
A) 2662.4 lb
B) 1331.2 lb
C) 665.6 lb
D) 332.8 lb

A) 2662.4 lb
B) 1331.2 lb
C) 665.6 lb
D) 332.8 lb

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
12
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 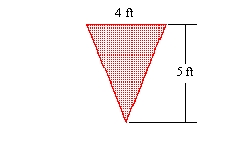
A) 104 lb
B) 1040 lb
C) 208 lb
D) 520 lb

A) 104 lb
B) 1040 lb
C) 208 lb
D) 520 lb

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose the average waiting time for a customer's call to be answered by a company representative (modeled by exponentially decreasing probability density functions) is minutes. Find the median waiting time.
A) minutes
B) minutes
C) minutes
D) minutes
E) minutes
A) minutes
B) minutes
C) minutes
D) minutes
E) minutes

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
14
The marginal cost function is defined to be the derivative of the cost function. If the marginal cost of manufacturing x units of a product is (measured in dollars per unit) and the fixed start-up cost is , use the Total Change Theorem to find the cost of producing the first 5,000 units.
A) $35,454,500
B) $35,484,500
C) $35,444,500
D) $35,434,500
E) $
A) $35,454,500
B) $35,484,500
C) $35,444,500
D) $35,434,500
E) $

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
15
Boxes are labeled as containing 500 g of cereal. The machine filling the boxes produces weights that are normally distributed with standard deviation 12
G) If the target weight is 500 g, what is the probability that the machine produces a box with less than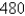 g of cereal? Round your answer to four decimal places.
g of cereal? Round your answer to four decimal places.
G) If the target weight is 500 g, what is the probability that the machine produces a box with less than
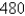 g of cereal? Round your answer to four decimal places.
g of cereal? Round your answer to four decimal places.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
16
For a given commodity and pure competition, the number of units produced and the price per unit are determined as the coordinates of the point of intersection of the supply and demand curves. Given the demand curve 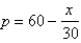 and the supply curve
and the supply curve 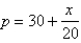 ,
,
find the consumer surplus.
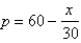 and the supply curve
and the supply curve 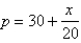 ,
,find the consumer surplus.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
17
The demand function for a commodity is given by . Find the consumer surplus when the sales level is .
A) $10458
B) $4458
C) $
D) $9458
E) $8458
A) $10458
B) $4458
C) $
D) $9458
E) $8458

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
18
The standard deviation for a random variable with probability density function f and mean µ is defined . Find the standard deviation for an exponential density function with mean .
A)
B)
C) 2
D)
E) 5
A)
B)
C) 2
D)
E) 5

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
19
For any normal distribution, find 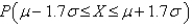 to two decimal places.
to two decimal places.
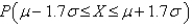 to two decimal places.
to two decimal places.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
20
The marginal revenue from producing x units of a certain product is (in dollars per unit). Find the increase in revenue if the production level is raised from 1,100 units to units.
A) $17765250
B) $
C) $26866667
D) $37974583
E) $51367000
A) $17765250
B) $
C) $26866667
D) $37974583
E) $51367000

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
21
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 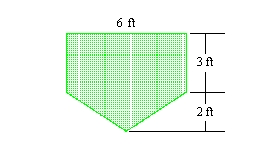


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
22
A trough is filled with a liquid of density 855 kg/ . The ends of the trough are equilateral triangles with sides 9 m long and vertex at the bottom. Find the hydrostatic force on one end of the trough.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
23
Find the exact coordinates of the centroid. 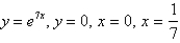
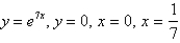

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
24
Find the coordinates of the centroid for the region bounded by the curves 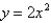 , x = 0,
, x = 0,
and y =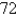 .
.
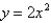 , x = 0,
, x = 0,and y =
 .
.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
25
Find the centroid of the region bounded by the given curves.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
26
An aquarium is 4 ft long, 3 ft wide, and 2 ft deep. If the aquarium is filled with water, find the force exerted by the water (a) on the bottom of the aquarium, (b) on the longer side of the aquarium, and (c) on the shorter side of the aquarium. (The weight density of water is 62.4 lb/ft3.)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
27
Use the Theorem of Pappus to find the volume of the solid obtained by revolving the region bounded by the graphs of and about the y-axis.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
28
Find the centroid of the region bounded by the graphs of the given equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
29
A swimming pool is 10 ft wide and 36 ft long and its bottom is an inclined plane, the shallow end having a depth of 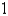 ft and the deep end, 12 ft. If the pool is full of water, find the hydrostatic force on the shallow end. (Use the fact that water weighs 62.5 lb/
ft and the deep end, 12 ft. If the pool is full of water, find the hydrostatic force on the shallow end. (Use the fact that water weighs 62.5 lb/ 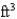 .)
.)
 ft and the deep end, 12 ft. If the pool is full of water, find the hydrostatic force on the shallow end. (Use the fact that water weighs 62.5 lb/
ft and the deep end, 12 ft. If the pool is full of water, find the hydrostatic force on the shallow end. (Use the fact that water weighs 62.5 lb/ 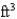 .)
.)
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
30
Find the centroid of the region bounded by the given curves.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
31
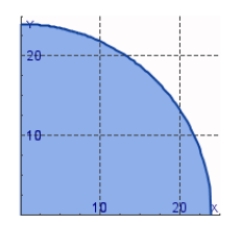
Find the center of mass of a lamina in the shape of a quarter-circle with radius 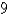 with density
with density 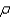 =
= 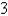 .
. 
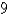 with density
with density 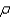 =
=  .
. 

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
32
A vertical plate is submerged in water (the surface of the water coincides with the x-axis). Find the force exerted by the water on the plate. (The weight density of water is 62.4 lb/ft3.) 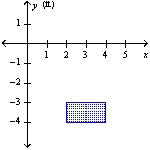 (ft)
(ft)
A) 62.4 lb
B) 873.6 lb
C) 436.8 lb
D) 124.8 lb
 (ft)
(ft)A) 62.4 lb
B) 873.6 lb
C) 436.8 lb
D) 124.8 lb

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
33
A rectangular tank has width 4 ft, height 4 ft, and length 7 ft. It is filled with equal volumes of water and oil. The oil has a weight density of 50 lb/ft3 and floats on the water. Find the force exerted by the mixture on one end of the tank. (The weight density of water is 62.4 lb/ft3.)
A) 1897.6 lb
B) 1699.2 lb
C) 899.2 lb
D) 1798.4 lb
A) 1897.6 lb
B) 1699.2 lb
C) 899.2 lb
D) 1798.4 lb

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
34
Find the centroid of the region bounded by the graphs of the given equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
35
Find the centroid of the region bounded by the given curves. 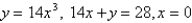
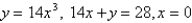

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
36
The masses are located at the point . Find the moments and and the center of mass of the system. ;
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the center of mass of the lamina with density  =
= 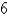 .
. 
 =
= 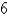 .
. 

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
38
Find the centroid of the region shown, not by integration, but by locating the centroids of the
rectangles and triangles and using additivity of moments.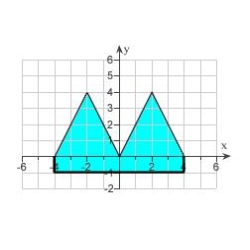
rectangles and triangles and using additivity of moments.


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
39
Find the centroid of the region bounded by the curves. 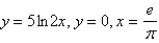
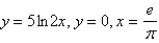

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
40
A trough has vertical ends that are equilateral triangles with sides of length 2 ft. If the trough is filled with water to a depth of 1 ft, find the force exerted by the water on one end of the trough. Round to one decimal place. (The weight density of water is 62.4 lb/ft3.)
A) 31.2 lb
B) 12.0 lb
C) 62.4 lb
D) 6.0 lb
A) 31.2 lb
B) 12.0 lb
C) 62.4 lb
D) 6.0 lb

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
41
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 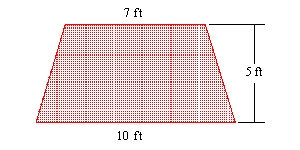


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
42
A vertical plate is submerged in water (the surface of the water coincides with the x-axis). Find the force exerted by the water on the plate. (The weight density of water is 62.4 lb/ft3.) 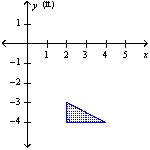 (ft)
(ft)
 (ft)
(ft)
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
43
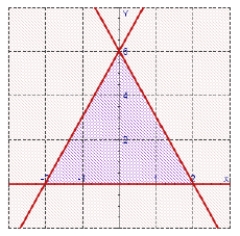
Find the centroid of the region shown in the figure. 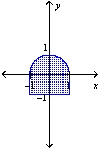


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
44
Find the volume obtained when the circle of radius 2 with center ( 2 , 0) is rotated about the y-axis.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
45
Find the area of the surface obtained by rotating the circle about the line .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
46
Find the area of the surface obtained by revolving the given curve about the x-axis. on
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
47
A vertical plate is submerged in water (the surface of the water coincides with the x-axis). Find the force exerted by the water on the plate. (The weight density of water is 62.4 lb/ft3.) 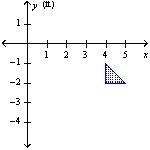 (ft)
(ft)
 (ft)
(ft)
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
48
Set up, but do not evaluate, an integral for the area of the surface obtained by rotating the curve about the x-axis on the interval .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
49
Find the centroid of the region bounded by the graphs of 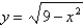 and
and 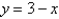 .
.
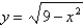 and
and 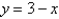 .
.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
50
A cylindrical drum of diameter 2 ft and length 6 ft is lying on its side, submerged in water 16 ft deep. Find the force exerted by the water on one end of the drum to the nearest pound. (The weight density of water is 62.4 lb/ft3.)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
51
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 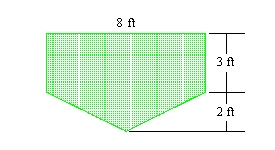


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
52
Set up, but do not evaluate, an integral for the area of the surface obtained by rotating the curve about the given axis. y-axis
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
53
Find the area of the surface obtained by rotating the curve about the y-axis.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
54
Find the area of the surface obtained by rotating the curve about the x-axis.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
55
Write an integral giving the area of the surface obtained by revolving the curve about the x-axis. (Do not evaluate the integral.) y = on [3, 6]
A) (![<strong>Write an integral giving the area of the surface obtained by revolving the curve about the x-axis. (Do not evaluate the integral.) y = \frac{4}{x} on [3, 6]</strong> A) (<font face=symbol></font> ) B) 8<font face=symbol></font> \int_{3}^{6} x^{3} \sqrt{x^{4}+16} d x C) 8<font face=symbol></font> \int_{3}^{6} \frac{\sqrt{x^{4}+16}}{x^{3}} d x D) (<font face=symbol></font> \int_{3}^{6} \frac{4}{x}\left(1+\left(-\frac{4}{x^{2}}\right)^{2}\right) d x )](https://storage.examlex.com/TB5972/11eaa3fc_bedc_3597_b1e4_35db679d46fd_TB5972_11.jpg) )
)
B) 8
C) 8
D) ( )
A) (
![<strong>Write an integral giving the area of the surface obtained by revolving the curve about the x-axis. (Do not evaluate the integral.) y = \frac{4}{x} on [3, 6]</strong> A) (<font face=symbol></font> ) B) 8<font face=symbol></font> \int_{3}^{6} x^{3} \sqrt{x^{4}+16} d x C) 8<font face=symbol></font> \int_{3}^{6} \frac{\sqrt{x^{4}+16}}{x^{3}} d x D) (<font face=symbol></font> \int_{3}^{6} \frac{4}{x}\left(1+\left(-\frac{4}{x^{2}}\right)^{2}\right) d x )](https://storage.examlex.com/TB5972/11eaa3fc_bedc_3597_b1e4_35db679d46fd_TB5972_11.jpg) )
)B) 8
C) 8
D) ( )

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
56
Find the area of the region under the graph of f on [a, b].
A) -3
B) -6
C) 6
D) 3
A) -3
B) -6
C) 6
D) 3

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
57
Find the centroid of the region bounded by the graphs of the given equations. 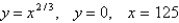
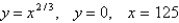

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
58
Find the center of mass of the lamina of the region shown if the density of the circular lamina is five times that of the rectangular lamina. 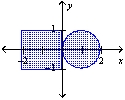


Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
59
Find the centroid of the region bounded by the graphs of 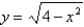 and
and 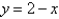 .
.
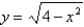 and
and 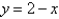 .
.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
60
Find the center of mass of the system comprising masses mk located at the points Pk in a coordinate plane. Assume that mass is measured in grams and distance is measured in centimeters.
m1 = 3, m2 = 4, m3 = 5
P1 (-3, 5), P2 (3, 4), P3 (-4, 1)
m1 = 3, m2 = 4, m3 = 5
P1 (-3, 5), P2 (3, 4), P3 (-4, 1)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
61
Find the length of the curve for the interval 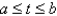 .
. 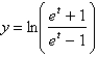
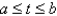 .
. 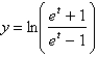

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
62
Find the area of the surface obtained by revolving the given curve about the y-axis.
x =![Find the area of the surface obtained by revolving the given curve about the y-axis. x = on [0, 2]](https://storage.examlex.com/TB5972/11eaa3fc_bedf_69f4_b1e4_b5e60fb926d5_TB5972_11.jpg) on [0, 2]
on [0, 2]
x =
![Find the area of the surface obtained by revolving the given curve about the y-axis. x = on [0, 2]](https://storage.examlex.com/TB5972/11eaa3fc_bedf_69f4_b1e4_b5e60fb926d5_TB5972_11.jpg) on [0, 2]
on [0, 2]
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
63
Find the area of the surface obtained by rotating the curve about the 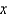 -axis.
-axis. 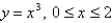
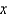 -axis.
-axis. 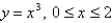

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
64
Set up, but do not evaluate, an integral that represents the length of the curve. 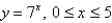
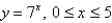

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
65
Use differentials to approximate the arc length of the graph of the equation from P to Q. Round answer to four decimal places. P (3, 12), Q (3.2, 13.24)
A) 6.0828
B) 3.6497
C) 1.2166
D) 2.4331
A) 6.0828
B) 3.6497
C) 1.2166
D) 2.4331

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
66
Find the arc length of the graph from A to B. 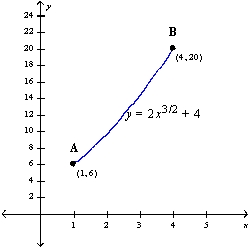
A) )
B) )
C) )
D) )

A) )
B) )
C) )
D) )

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
67
Set up, but do not evaluate, an integral for the length of the curve. 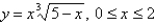
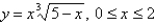

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
68
Find the length of the curve.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
69
Find the length of the curve.
A) 13.05
B) 25.05 5
C)
D) 36.05
E) None of these
A) 13.05
B) 25.05 5
C)
D) 36.05
E) None of these

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
70
Find the length of the curve for the interval .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
71
Find the length of the curve.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
72
Find the length of the line segment joining the two given points by finding the equation of the line using Equation (2). Then check your answer by using the distance formula. (0, 0), (1, 8)
A)
B) 9
C)
D) 3
A)
B) 9
C)
D) 3

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
73
Find the area of the surface obtained by revolving the graph of y = ![Find the area of the surface obtained by revolving the graph of y = on [0, 1] about the x-axis.](https://storage.examlex.com/TB5972/11eaa3fc_bedf_df25_b1e4_159b174fd3b1_TB5972_11.jpg) on [0, 1] about the x-axis.
on [0, 1] about the x-axis.
![Find the area of the surface obtained by revolving the graph of y = on [0, 1] about the x-axis.](https://storage.examlex.com/TB5972/11eaa3fc_bedf_df25_b1e4_159b174fd3b1_TB5972_11.jpg) on [0, 1] about the x-axis.
on [0, 1] about the x-axis.
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
74
Find the arc length of the graph of the given equation on the specified interval. y = ( + 1)
, [2, 5]
A)
B)
C)
D)
, [2, 5]
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
75
Find the area of the surface obtained by revolving the given curve about the x-axis. ![Find the area of the surface obtained by revolving the given curve about the x-axis. on [0, 1]](https://storage.examlex.com/TB5972/11eaa3fc_bee0_5456_b1e4_1356f4856f0e_TB5972_11.jpg) on [0, 1]
on [0, 1]
![Find the area of the surface obtained by revolving the given curve about the x-axis. on [0, 1]](https://storage.examlex.com/TB5972/11eaa3fc_bee0_5456_b1e4_1356f4856f0e_TB5972_11.jpg) on [0, 1]
on [0, 1]
Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
76
If the infinite curve , is rotated about the x-axis , find the area of the resulting surface.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
77
Use Simpson's Rule with n = 6 to estimate the length of the curve , . Round your answer to six decimal places.
A) 6.987208
B) 6.947368
C) 6.972089
D) 6.947582
E) None of these
A) 6.987208
B) 6.947368
C) 6.972089
D) 6.947582
E) None of these

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
78
Set up, but do not evaluate, an integral for the length of the curve.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
79
Find the arc length function for the curve with starting point .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
80
A hawk flying at an altitude of m accidentally drops its prey. The parabolic trajectory of the falling prey is described by the equation until it hits the ground, where y is its height above the ground and x is the horizontal distance traveled in meters.
True or False?
The distance traveled by the prey from the time it is dropped until the time it hits the ground is
approximately m.
True or False?
The distance traveled by the prey from the time it is dropped until the time it hits the ground is
approximately m.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck


