Exam 8: Further Applications of Integration
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Write an integral giving the area of the surface obtained by revolving the curve about the x-axis. (Do not evaluate the integral.) y = on [3, 6]
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
C
Set up, but do not evaluate, an integral for the length of the curve.
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
E
A trough has vertical ends that are equilateral triangles with sides of length 2 ft. If the trough is filled with water to a depth of 1 ft, find the force exerted by the water on one end of the trough. Round to one decimal place. (The weight density of water is 62.4 lb/ft3.)
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
B
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 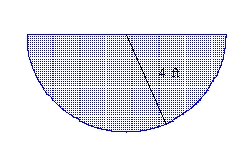
(Multiple Choice)
4.9/5  (34)
(34)
For the following exercise, (a) plot the graph of the function f, (b) write an integral giving the arc length of the graph of the function over the indicated interval, and (c) find the arc length of the curve accurate to two decimal places. = x - 3 ; [0, 3]
(Short Answer)
4.8/5  (34)
(34)
Find the centroid of the region bounded by the given curves.
(Multiple Choice)
4.9/5  (39)
(39)
Find the area of the surface obtained by rotating the curve about the -axis.
on [0, 2]
(Short Answer)
4.9/5  (40)
(40)
The manager of a fast-food restaurant determines that the average time that her customers wait for service is 2 minutes. Find the probability that a customer is served within the first 2 minutes.
(Multiple Choice)
5.0/5  (33)
(33)
Find the area of the surface obtained by rotating the circle about the line .
(Multiple Choice)
4.9/5  (42)
(42)
Use Simpson's Rule with n = 6 to estimate the length of the curve , . Round your answer to six decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
A demand curve is given by .
Find the consumer surplus when the selling price is $ .
(Short Answer)
4.8/5  (43)
(43)
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 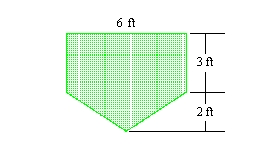
(Short Answer)
4.8/5  (42)
(42)
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is 62.4 lb/ft3.) 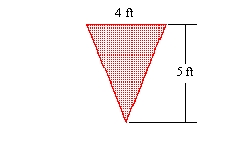
(Multiple Choice)
4.8/5  (27)
(27)
The demand function for a commodity is given by . Find the consumer surplus when the sales level is .
(Multiple Choice)
4.9/5  (27)
(27)
Use differentials to approximate the arc length of the graph of the equation from P to Q. Round answer to four decimal places. P (3, 12), Q (3.2, 13.24)
(Multiple Choice)
4.8/5  (39)
(39)
A vertical plate is submerged in water (the surface of the water coincides with the x-axis). Find the force exerted by the water on the plate. (The weight density of water is 62.4 lb/ft3.) 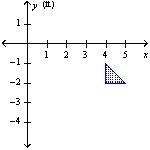 (ft)
(ft)
(Short Answer)
4.8/5  (33)
(33)
Find the centroid of the region shown, not by integration, but by locating the centroids of the
rectangles and triangles and using additivity of moments. 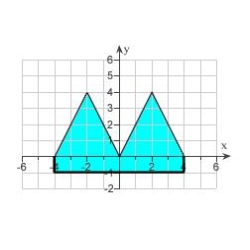
(Short Answer)
4.8/5  (36)
(36)
Showing 1 - 20 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)