Deck 6: Inverse Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/95
Play
Full screen (f)
Deck 6: Inverse Functions
1
If 10 J of work are needed to stretch a spring from 10 cm to 12 cm and another 20 J are needed to stretch it from 12 cm to 14 cm, what is the natural length of the spring? Round the answer to nearest integer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Find the average value of the function on the given interval. 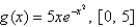
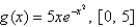
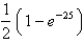
3
Find the volume of the solid obtained by revolving the region under the graph of 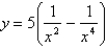 on [1,
on [1, 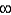 ) about the x-axis.
) about the x-axis.
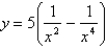 on [1,
on [1, 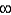 ) about the x-axis.
) about the x-axis.not answered
4
In a certain city the temperature hours after 7 A.M. was modeled by the function Find the average temperature to three decimal places during the period from 7 A.M. to 7 P.M.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
5
A force of 30 N is required to maintain a spring stretched from its natural length of 12 cm to a length of 15 cm. How much work is done in stretching the spring from 11 cm to 24 cm?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
6
A bucket weighs 7 lb and a rope of negligible weight are used to draw water from a well that is 60 ft deep. The bucket starts with 50 lb of water and is pulled up at a rate of 10 ft/s, but water leaks out of a hole in the bucket at a rate of 0.5 lb/s. Find the work done in pulling the bucket to the top of the well.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
7
Find the number(s) a such that the average value of the function 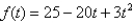 on the interval
on the interval 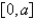 is equal to
is equal to 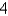 .
.
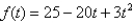 on the interval
on the interval 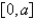 is equal to
is equal to 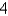 .
.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
8
Find the average value of the function on the given interval.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
9
Find the average value of the function 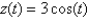 on the interval
on the interval 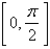 .
.
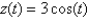 on the interval
on the interval 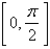 .
.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
10
A tank is full of water. Find the work required to pump the water out of the outlet. 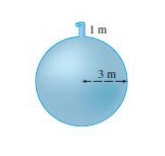
A)
B)
C)
D)
E) None of these

A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
11
Find the average value of the function on the interval . Round your answer to 3 decimal places.
A) 9.342
B) 0.45
C) 0.432
D)
E) 18
A) 9.342
B) 0.45
C) 0.432
D)
E) 18

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
12
A spring has a natural length of 20 cm. If a force of 25 N is required to keep it stretched to a length of 30 cm, how much work is required to stretch it from 20 cm to 32 cm?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
13
The Mean Value Theorem for Integrals says that if is continuous on [ , ], then there exists a number m in [ , ] such that

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
14
The linear density of a m long rod is where x is measured in meters from one end of the rod. Find the average density of the rod.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
15
A heavy rope, 40 ft long, weighs lb/ft and hangs over the edge of a building 110 ft high. How much work is done in pulling the rope to the top of the building?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
16
Find the average value of the function on the interval .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
17
The temperature of a metal rod, 6 m long, is 5 x (in degree Celsius) at a distance x meters from one end of the rod. What is the average temperature of the rod?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
18
Find the number(s) a such that the average value of the function on the interval is equal to 10.
A)
B)
C)
D)
E) .
A)
B)
C)
D)
E) .

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
19
Newton's Law of Gravitation states that two bodies with masses attract each other with a force where r is the distance between the bodies and G is the gravitation constant. If one of bodies is fixed, find the work needed to move the other from to .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
20
The velocity v of blood that flows in a blood vessel with radius 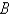 and length l at a distance
and length l at a distance 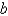 from the central axis is
from the central axis is 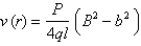 where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval
where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval 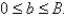
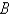 and length l at a distance
and length l at a distance 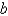 from the central axis is
from the central axis is 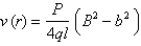 where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval
where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval 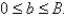

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
21
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y =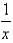 , y = 0, x = 2, x = 5; the y-axis
, y = 0, x = 2, x = 5; the y-axis
y =
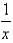 , y = 0, x = 2, x = 5; the y-axis
, y = 0, x = 2, x = 5; the y-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose you make napkin rings by drilling holes with different diameters through two wooden balls (which also have different diameters). You discover that both napkin rings have the same height h as shown in the figure. Use cylindrical shells to compute the volume of a napkin ring created by drilling a hole with radius d through the center of a sphere of radius D and express the answer in terms of . 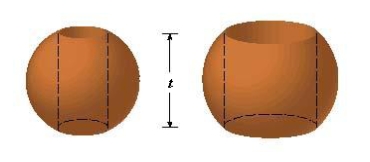
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
23
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = 3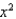 , y = 0, x = 1; the y-axis
, y = 0, x = 1; the y-axis
y = 3
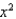 , y = 0, x = 1; the y-axis
, y = 0, x = 1; the y-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
24
Use cylindrical shells to find the volume of the solid. A sphere of radius .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
25
An aquarium 6 m long, 1 m wide, and 1 m deep is full of water. Find the work needed to pump half of the water out of the aquarium. (Use the facts that the density of water is )
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
26
If a force of 6 lbs is required to hold a spring stretched 5 inches beyond its natural length, then 38.4 lb-in. of work is done in stretching it from its natural length to 8 in. beyond its natural length.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
27
Use the Midpoint Rule with n = 4 to estimate the volume obtained by rotating about the region under the y-axis the region under the curve. Select the correct answer. The choices are rounded to the nearest hundredth.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
28
Use a graphing utility to (a) plot the graphs of the given functions, (b) find the approximate x-coordinates of the points of intersection of the graphs, and (c) find an approximation of the volume of the solid obtained by revolving the region bounded by the graphs of the functions about the y-axis. Round answers to two decimal places.
y = x, y = - , x 0
y = x, y = - , x 0

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
29
A particle moves a distance of 150 ft along a straight line. As it moves, it is acted upon by a constant force of magnitude 15 lb in a direction opposite to that of the motion. What is the work done by the force?
A) ft-lb
B) ft-lb
C) -2250 ft-lb
D) ft-lb
A) ft-lb
B) ft-lb
C) -2250 ft-lb
D) ft-lb

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
30
In a steam engine the pressure and volume of steam satisfy the equation 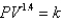 , where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of
, where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of 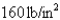 and a volume of
and a volume of 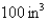 and expands to a volume of
and expands to a volume of 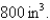 Use the fact that the work done by the gas when the volume expands from
Use the fact that the work done by the gas when the volume expands from 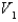 to volume
to volume 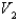 is
is 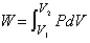 .
.
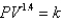 , where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of
, where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of 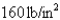 and a volume of
and a volume of 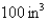 and expands to a volume of
and expands to a volume of 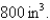 Use the fact that the work done by the gas when the volume expands from
Use the fact that the work done by the gas when the volume expands from 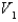 to volume
to volume 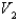 is
is 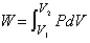 .
.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
31
Use the method of cylindrical shells to find the volume of solid obtained by rotating the region bounded by the given curves about the x-axis.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
32
Use the method of disks or washers, or the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle. , , , the x-axis
A)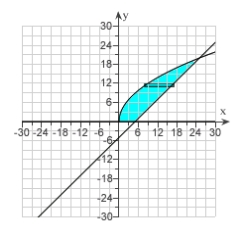
B)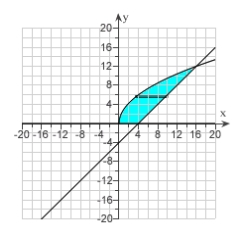
C)
D)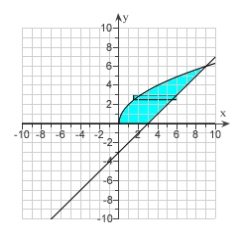
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
33
Find the work done in pushing a car a distance of 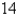 m while exerting a constant force of
m while exerting a constant force of 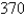 N.
N.
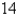 m while exerting a constant force of
m while exerting a constant force of  N.
N.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
34
The base of a solid is a circular disk with radius 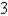 . Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
. Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
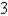 . Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
. Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
35
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated line. Sketch the region and a representative rectangle. y = 25 - , y = 0; the line x = - 5
A)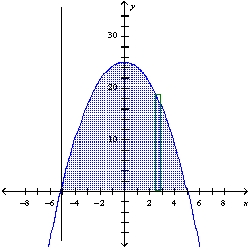
B)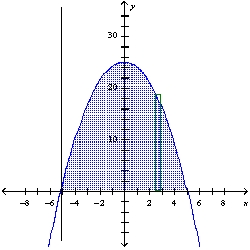
C)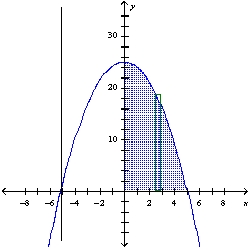
D)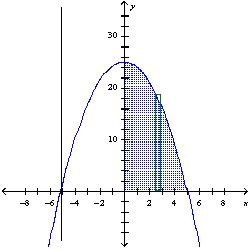
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
36
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. 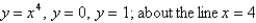
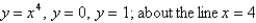

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
37
Use the method of disks or washers, or the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = 2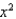 , y = 4x - 2, y = 8; the y-axis
, y = 4x - 2, y = 8; the y-axis
y = 2
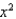 , y = 4x - 2, y = 8; the y-axis
, y = 4x - 2, y = 8; the y-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
38
Use the method of cylindrical shells to find the volume of solid obtained by rotating the region bounded by the given curves about the x-axis. 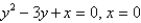
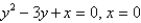

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
39
Sketch a plane region and indicate the axis about which it is revolved so that the resulting solid of revolution (found using the shell method) is given by the integral. 2
A)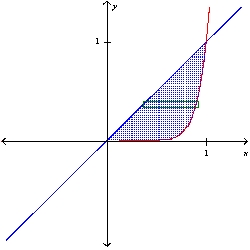 x-axis
x-axis
B)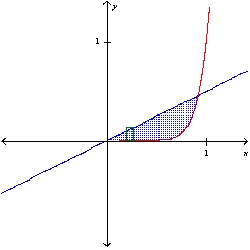 y-axis
y-axis
C)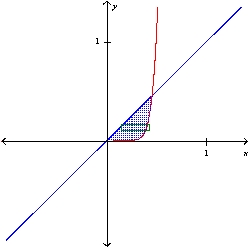 x-axis
x-axis
D)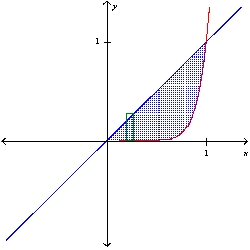 y-axis
y-axis
A)
 x-axis
x-axisB)
 y-axis
y-axisC)
 x-axis
x-axisD)
 y-axis
y-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
40
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle. y = , y = -x + 4; the y-axis
A)
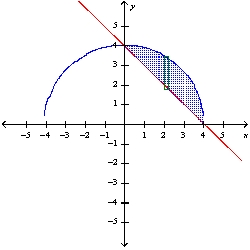
B) 128
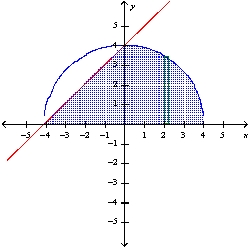
C) 128
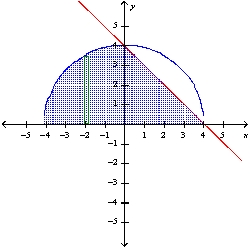
D)
A)

B) 128

C) 128

D)


Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
41
The height of a monument is m. A horizontal cross-section at a distance x meters from the top is an equilateral triangle with side meters. Find the volume of the monument.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
42
Sketch a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information to estimate the volume of the solid obtained by rotating about the y axis the region enclosed by these curves. Rounded to the nearest hundredth.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
43
The base of S is a circular region with boundary curve 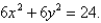 Cross-sections perpendicular to the x axis are isosceles right triangles with hypotenuse in the base.
Cross-sections perpendicular to the x axis are isosceles right triangles with hypotenuse in the base.
Find the volume of S.
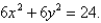 Cross-sections perpendicular to the x axis are isosceles right triangles with hypotenuse in the base.
Cross-sections perpendicular to the x axis are isosceles right triangles with hypotenuse in the base.Find the volume of S.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
44
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
45
Find the volume of the solid obtained by rotating the region bounded by about the x-axis.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
46
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated line. y = 4 - , y = 0; the line y = 5
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
47
Find the volume of the solid obtained by rotating the region bounded by about the line
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
48
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated line. Sketch the region and a representative rectangle.
y =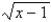 , y = x - 1; the line x = 2
, y = x - 1; the line x = 2
y =
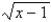 , y = x - 1; the line x = 2
, y = x - 1; the line x = 2
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
49
Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. 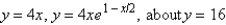
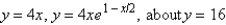

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
50
The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. about the y-axis
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
51
Find the volume common to two spheres, each with radius r = 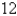 if the center of each sphere lies on the surface of the other sphere.
if the center of each sphere lies on the surface of the other sphere.
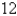 if the center of each sphere lies on the surface of the other sphere.
if the center of each sphere lies on the surface of the other sphere.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
52
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis. y = cos x + 1, x = 0, y = 0, x =
A) + 2
B) + 4
C)
+ 4
D)
+2
A) + 2
B) + 4
C)
+ 4
D)
+2

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
53
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations and inequalities about the y-axis. - = 16, x 0, y = - 4, y = 4
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
54
Find the volume of the solid that is obtained by revolving the region about the line y = . 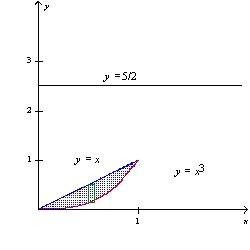
A)
B)
C)
D) 89

A)
B)
C)
D) 89

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
55
Use the method of disks or washers, or the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y =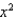 , y = 2x - 1, y = 4; the y-axis
, y = 2x - 1, y = 4; the y-axis
y =
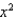 , y = 2x - 1, y = 4; the y-axis
, y = 2x - 1, y = 4; the y-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
56
The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. Round your answer to 3 decimal places. about the y-axis and .
A) 1763.213
B) None of these
C) 1752.016
D) 1760.025
E) 880.012
A) 1763.213
B) None of these
C) 1752.016
D) 1760.025
E) 880.012

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
57
Find the volume of a pyramid with height 4 and base an equilateral triangle with side a = 4 . 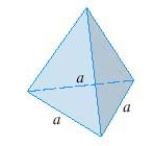
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
58
Find the volume of the solid that is obtained by revolving the region about the x-axis. 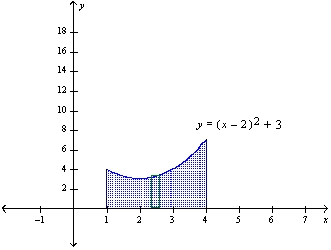
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
59
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
A)
B)
C)
D)
E) None
A)
B)
C)
D)
E) None

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
60
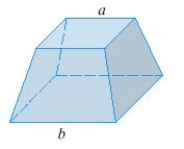
Find the volume of the frustum of a pyramid with square base of side 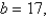 square top of side
square top of side 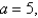 and height
and height 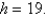
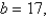 square top of side
square top of side 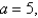 and height
and height 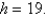


Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
61
The base of S is the parabolic region 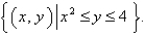 Cross-sections perpendicular to the y axis are squares.
Cross-sections perpendicular to the y axis are squares.
Find the volume of S.
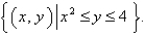 Cross-sections perpendicular to the y axis are squares.
Cross-sections perpendicular to the y axis are squares.Find the volume of S.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
62
Find the volume of the solid obtained by rotating the region bounded by 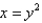 and
and 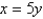 about the y-axis.
about the y-axis.
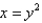 and
and 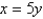 about the y-axis.
about the y-axis.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
63
Sketch a plane region, and indicate the axis about which it is revolved so that the resulting solid of revolution has the volume given by the integral. 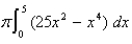
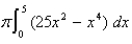

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
64
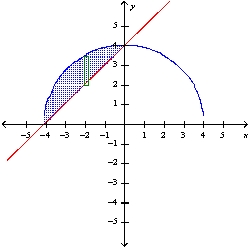
Find the area of the shaded region. 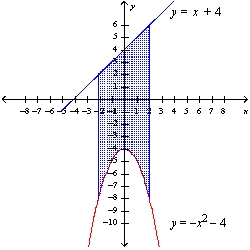
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
65
Graph the region between the curves and use your calculator to compute the area correct to five decimal places.
A) 12.08127
B) 91.504
C) 3.141257
D) 3.66016
E) 18.3008
A) 12.08127
B) 91.504
C) 3.141257
D) 3.66016
E) 18.3008

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
66
Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. 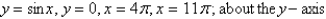
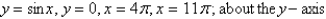

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
67
Find the area of the region bounded by the given curves.
A)
B)
C) 4
D) 2
E)
A)
B)
C) 4
D) 2
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
68
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. 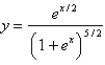 ,
, 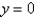 ,
, 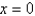 ,
, 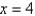 ; the x-axis
; the x-axis
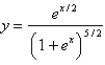 ,
, 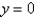 ,
, 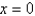 ,
, 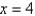 ; the x-axis
; the x-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
69
Find the volume of the solid obtained by rotating about the x-axis the region under the curve 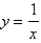 from x =
from x = 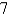 to x =
to x = 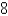 .
.
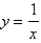 from x =
from x = 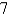 to x =
to x = 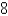 .
.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
70
Find the volume of the solid obtained by rotating the region bounded by 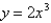 and
and 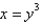 about the line
about the line 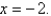
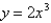 and
and 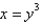 about the line
about the line 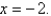

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
71
Find the area of the shaded region. 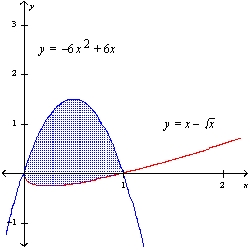
A) 7
B)
C)
D)

A) 7
B)
C)
D)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
72
Find the number b such that the line divides the region bounded by the curves and into two regions with equal area.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
73
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. 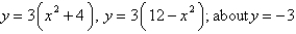
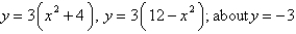

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
74
Find the volume of a cap of a sphere with radius r = 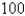 and height h = 3
and height h = 3 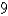 .
. 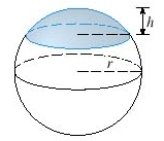
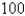 and height h = 3
and height h = 3 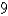 .
. 

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
75
Find the area of the region bounded by the given curves.
A)
B) None of these
C)
D)
E)
A)
B) None of these
C)
D)
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
76
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle. 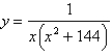 , y = 0, x = 1, x = 12; the y-axis
, y = 0, x = 1, x = 12; the y-axis
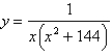 , y = 0, x = 1, x = 12; the y-axis
, y = 0, x = 1, x = 12; the y-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
77
The volume of a solid torus (the donut-shaped solid shown in the figure) with r = 5 and R = 15 is 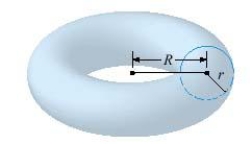


Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
78
Use a graphing utility to (a) plot the graphs of the given functions and (b) find the approximate x-coordinates of the points of intersection of the graphs. Then find an approximation of the volume of the solid obtained by revolving the region bounded by the graphs of the functions about the x-axis. Round answers to two decimal places.
y =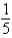
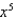 , y = 3
, y = 3 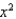 -
- 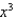
y =
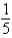
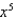 , y = 3
, y = 3 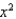 -
- 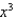

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
79
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis.
y =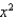 , y = 0, x = 3, x = 5; the x-axis
, y = 0, x = 3, x = 5; the x-axis
y =
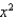 , y = 0, x = 3, x = 5; the x-axis
, y = 0, x = 3, x = 5; the x-axis
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
80
Find the area of the region bounded by the given curves.
A)
B)
C)
D)
E) 6
A)
B)
C)
D)
E) 6

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck


