Exam 6: Inverse Functions
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the values of c such that the area of the region bounded by the parabolas is .
Free
(Short Answer)
4.8/5  (33)
(33)
Correct Answer:
The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. about the y-axis
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
A
Racing cars driven by Chris and Kelly are side by side at the start of a race. The table shows the velocities of each car (in miles per hour) during the first ten seconds of the race. Use the Midpoint Rule to estimate how much farther Kelly travels than Chris does during the first ten seconds. t 0 0 0 1 22 28 2 33 38 3 45 46 4 53 60 5 63 69 6 72 83 7 78 83 8 85 97 9 90 98 10 90 102
Free
(Short Answer)
4.9/5  (32)
(32)
Correct Answer:
ft
Find the work done in pushing a car a distance of 14 m while exerting a constant force of 370 N.
(Short Answer)
4.8/5  (35)
(35)
Find the volume common to two spheres, each with radius r = if the center of each sphere lies on the surface of the other sphere.
(Short Answer)
4.8/5  (36)
(36)
The base of S is the parabolic region Cross-sections perpendicular to the y axis are squares.
Find the volume of S.
(Short Answer)
4.7/5  (44)
(44)
Use the method of disks or washers, or the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle. , , , the x-axis
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of a cap of a sphere with radius r = and height h = 3 9 . 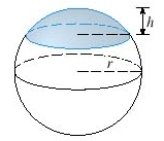
(Short Answer)
4.9/5  (37)
(37)
Use a graphing utility to (a) plot the graphs of the given functions, (b) find the approximate x-coordinates of the points of intersection of the graphs, and (c) find an approximation of the volume of the solid obtained by revolving the region bounded by the graphs of the functions about the y-axis. Round answers to two decimal places.
y = x, y = - , x 0
(Short Answer)
4.9/5  (40)
(40)
Use the method of disks or washers, or the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = , y = 2x - 1, y = 4; the y-axis
(Short Answer)
4.8/5  (33)
(33)
Find the volume of a pyramid with height 4 and base an equilateral triangle with side a = 4 . 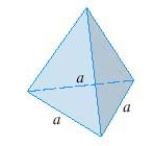
(Multiple Choice)
4.8/5  (39)
(39)
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis.
(Short Answer)
4.8/5  (41)
(41)
Find the average value of the function on the interval . Round your answer to 3 decimal places.
(Multiple Choice)
4.7/5  (40)
(40)
The height of a monument is m. A horizontal cross-section at a distance x meters from the top is an equilateral triangle with side meters. Find the volume of the monument.
(Multiple Choice)
4.8/5  (37)
(37)
Find the volume of the solid obtained by rotating about the x-axis the region under the curve from x = 7 to x = 8 .
(Short Answer)
4.8/5  (46)
(46)
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = , y = 0, x = 2, x = 5; the y-axis
(Short Answer)
4.8/5  (39)
(39)
Showing 1 - 20 of 95
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)