Deck 3: Applications of Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/155
Play
Full screen (f)
Deck 3: Applications of Differentiation
1
Find the derivative of the function. = sinh 4x
A) -4 cosh 4x
B) 4 sinh 4x
C) -sinh 4x
D) 4 cosh 4x
A) -4 cosh 4x
B) 4 sinh 4x
C) -sinh 4x
D) 4 cosh 4x
4 cosh 4x
2
Find the given integral.
A) -sinh (9x + 5)+ C
B) 9sinh (9x + 5) + C
C) sinh (9x + 5)+ C
D) sinh (9x + 5) + C
A) -sinh (9x + 5)+ C
B) 9sinh (9x + 5) + C
C) sinh (9x + 5)+ C
D) sinh (9x + 5) + C
sinh (9x + 5) + C
3
Find the derivative of 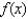 .
. 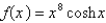
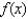 .
. 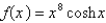
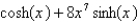
4
A telephone line hangs between two poles at 12 m apart in the shape of the catenary , where x and y are measured in meters. Find the slope of this curve where it meets the right pole. 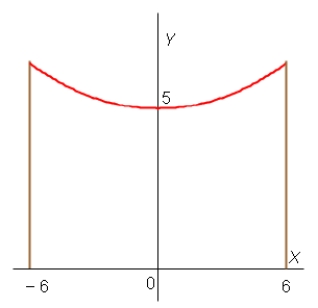
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
5
Two sides of a triangle are 2 m and 3 m in length and the angle between them is increasing at a rate of rad/s. Find the rate at which the area of the triangle is increasing when the
Angle between the sides of fixed length is ( )
A)
B)
C)
D)
E)
Angle between the sides of fixed length is ( )
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
6
Find the derivative of the function.  = sinh -1 6x
= sinh -1 6x
 = sinh -1 6x
= sinh -1 6x
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
7
Determine the values of x for which the given linear approximation is accurate to within 0.07 at a = 0.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
8
Use the linear approximation of the function at to approximate the number .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
9
A turkey is removed from the oven when its temperature reaches and is placed on a table in a room where the temperature is . After 10 minutes the temperature of the turkey is and after 20 minutes it is . Use a linear approximation to predict the temperature of the turkey after minutes.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
10
The top of a ladder slides down a vertical wall at a rate of m/s . At the moment when the bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s . How long is the ladder?
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
11
Find the derivative of the function. = cosh2 (6t2 + 3)
A) 24t sinh (6t2 + 3)
B) 24t cosh (6t2 + 3) sinh (6t2 + 3)
C) 12t sinh (6t2 + 3)
D) 12t cosh (6t2 + 3) sinh (6t2 + 3)
A) 24t sinh (6t2 + 3)
B) 24t cosh (6t2 + 3) sinh (6t2 + 3)
C) 12t sinh (6t2 + 3)
D) 12t cosh (6t2 + 3) sinh (6t2 + 3)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
12
Find the value of the expression accurate to four decimal places. sinh 4
A) 55.5798
B) 15.145
C) 27.2899
D) 29.3082
A) 55.5798
B) 15.145
C) 27.2899
D) 29.3082

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate 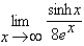
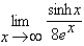

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
14
Gravel is being dumped from a conveyor belt at a rate of 32 ft/min and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10 ft high? Round the result to the nearest hundredth. 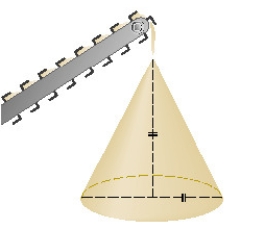
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
15
If two resistors with resistances and are connected in parallel, as in the figure, then the total resistance measured in ohms ( ), is given by . If and are increasing at rates of and respectively, how fast is changing when and ?
Round the result to the nearest thousandth.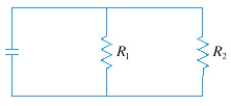
A)
B)
C)
D)
E)
Round the result to the nearest thousandth.

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
16
Find the derivative of the function. y =
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
17
Use differentials to estimate the amount of paint needed to apply a coat of paint cm thick to a hemispherical dome with diameter m.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
18
A plane flying horizontally at an altitude of 1 mi and a speed of mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
19
The circumference of a sphere was measured to be  cm with a possible error of
cm with a possible error of 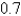 cm. Use differentials to estimate the maximum error in the calculated volume.
cm. Use differentials to estimate the maximum error in the calculated volume.
 cm with a possible error of
cm with a possible error of 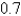 cm. Use differentials to estimate the maximum error in the calculated volume.
cm. Use differentials to estimate the maximum error in the calculated volume.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
20
Two cars start moving from the same point. One travels south at mi/h and the other travels west at mi/h. At what rate is the distance between the cars increasing 2 hours later? Round the result to the nearest hundredth.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
21
The volume of a cube is increasing at a rate of 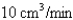 . How fast is the surface area increasing when the length of an edge is
. How fast is the surface area increasing when the length of an edge is 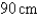 .
.
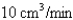 . How fast is the surface area increasing when the length of an edge is
. How fast is the surface area increasing when the length of an edge is 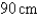 .
.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
22
The quantity Q of charge in coulombs C that has passed through a point in a wire up to time t (measured in seconds) is given by . Find the current when .
A) 15
B) 24
C) 26
D) 18
E) 13
A) 15
B) 24
C) 26
D) 18
E) 13

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
23
The top of a ladder leaning against a wall is 8 ft above the ground. The slope of the ladder with respect to the ground is -4. What is the length of the ladder?

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
24
Water flows from a tank of constant cross-sectional area 50 through an orifice of constant cross-sectional area located at the bottom of the tank. Initially, the height of the water in the tank was 20 ft, and t sec later it was given by the equation How fast was the height of the water decreasing when its height was 2 ft? 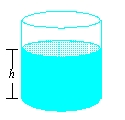
A) ft/sec
B) ft/sec.
C) ft/sec
D) ft/sec

A) ft/sec
B) ft/sec.
C) ft/sec
D) ft/sec

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
25
The altitude of a triangle is increasing at a rate of 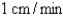 while the area of the triangle is increasing at a rate of
while the area of the triangle is increasing at a rate of 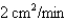 . At what rate is the base of the triangle changing when the altitude is 10 cm and the area is
. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 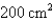 .
.
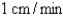 while the area of the triangle is increasing at a rate of
while the area of the triangle is increasing at a rate of 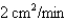 . At what rate is the base of the triangle changing when the altitude is 10 cm and the area is
. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 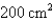 .
.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose the daily total cost (in dollars) of manufacturing x televisions is What is the marginal cost when x = 300? What is the actual cost incurred in manufacturing the 301st television?
A) $195.33, $195.42
B) $220.00, $220.28
C) $195.33, $195.98
D) $220.00, $220.73
A) $195.33, $195.42
B) $220.00, $220.28
C) $195.33, $195.98
D) $220.00, $220.73

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
27
Find the average rate of change of the area of a circle with respect to its radius r as r changes from 5 to 6 .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
28
In an adiabatic process (one in which no heat transfer takes place), the pressure P and volume V of an ideal gas such as oxygen satisfy the equation , where C is a constant. Suppose that at a certain instant of time, the volume of the gas is 2L, the pressure is 100 kPa, and the pressure is decreasing at the rate of 5 kPa/sec. Find the rate at which the volume is changing.
A) 14 L/sec
B) 14 L/sec
C) L/sec
D) L/sec
A) 14 L/sec
B) 14 L/sec
C) L/sec
D) L/sec

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
29
The parents of a child wish to establish a trust fund for the child's college education. If they need an estimated $90,000 5 years from now and they are able to invest the money at 5.5% compounded continuously in the interim, how much should they set aside in trust now?
A) $68,361.49
B) $17,061.61
C) $17,036.73
D) $68,862.09
A) $68,361.49
B) $17,061.61
C) $17,036.73
D) $68,862.09

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
30
If a snowball melts so that its surface area decreases at a rate of 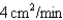 , find the rate at which the diameter decreases when the diameter is
, find the rate at which the diameter decreases when the diameter is 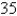 cm.
cm.
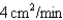 , find the rate at which the diameter decreases when the diameter is
, find the rate at which the diameter decreases when the diameter is 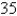 cm.
cm.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
31
A water trough is 20 m long and a cross-section has the shape of an isosceles trapezoid that is 20 cm wide at the bottom, 60 cm wide at the top, and has height 50 cm. If the trough is being filled with water at the rate of 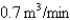 , how fast is the water level rising when the water is
, how fast is the water level rising when the water is 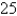 cm deep? Round the result to the nearest hundredth.
cm deep? Round the result to the nearest hundredth.
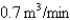 , how fast is the water level rising when the water is
, how fast is the water level rising when the water is 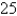 cm deep? Round the result to the nearest hundredth.
cm deep? Round the result to the nearest hundredth.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
32
A baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward first base with a speed of 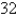 ft/s. At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
ft/s. At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
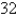 ft/s. At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
ft/s. At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
33
If two resistors with resistances and are connected in parallel, as in the figure, then the total resistance measured in ohms ( ), is given by . If and are increasing at rates of and respectively, how fast is changing when and ?
Round your answer to the nearest thousandth.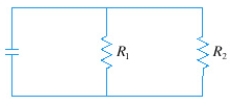
A)
B)
C)
D)
E)
Round your answer to the nearest thousandth.

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
34
Two carts, A and B, are connected by a rope 39 ft long that passes over a pulley (see the figure below). The point Q is on the floor 12 ft directly beneath and between the carts. Cart A is being pulled away from Q at a speed of 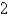 ft/s. How fast is cart B moving toward Q at the instant when cart A is 5 ft from Q?
ft/s. How fast is cart B moving toward Q at the instant when cart A is 5 ft from Q? 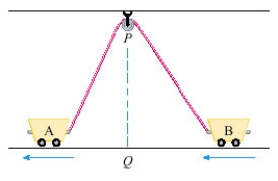
 ft/s. How fast is cart B moving toward Q at the instant when cart A is 5 ft from Q?
ft/s. How fast is cart B moving toward Q at the instant when cart A is 5 ft from Q? 

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
35
The equation of motion is given for a particle, where s is in meters and t is in seconds. Find the acceleration after seconds.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
36
Find the rate of change of y with respect of x at the indicated value of x. t = csc x - 18 cos x;
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
37
Find an equation of the tangent line to the curve at the point (4,1).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
38
The mass of the part of a metal rod that lies between its left end and a point x meters to the right is . Find the linear density when x is 3 m.
A) 4
B) 20
C) 24
D) 12
E) 18
A) 4
B) 20
C) 24
D) 12
E) 18

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
39
Find the accumulated amount after 7 years on an investment of $2,000 earning an interest rate of 5% per year compounded continuously. Round to the nearest cent.
A) $2,814.20
B) $2,838.14
C) $14,700.00
D) $14,717.80
A) $2,814.20
B) $2,838.14
C) $14,700.00
D) $14,717.80

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
40
A boat is pulled into a dock by a rope attached to the bow of the boat and passing through a pulley on the dock that is 1 m higher than the bow of the boat. If the rope is pulled in at a rate of 1 m/s how fast is the boat approaching the dock when it is 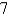 m from the dock? Round the result to the nearest hundredth if necessary.
m from the dock? Round the result to the nearest hundredth if necessary. 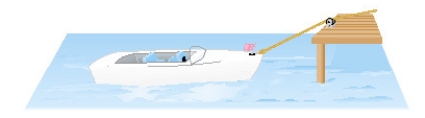
 m from the dock? Round the result to the nearest hundredth if necessary.
m from the dock? Round the result to the nearest hundredth if necessary. 

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
41
A spherical balloon is being inflated. Find the rate of increase of the surface area 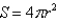 with respect to the radius r when r =
with respect to the radius r when r = 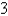 ft.
ft.
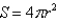 with respect to the radius r when r =
with respect to the radius r when r = 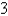 ft.
ft.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
42
The height (in meters) of a projectile shot vertically upward from a point m above ground level with an initial velocity of 25.48 m/s is after t seconds.
a. When does the projectile reach its maximum height?
b. What is the maximum height?
A)
B)
C)
D)
E)
a. When does the projectile reach its maximum height?
b. What is the maximum height?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose that f and g are functions that are differentiable at x = 2 and that f (2) = -1, 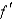 (2) = 3, g(2) = 3, and
(2) = 3, g(2) = 3, and 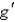 (2) = -4. Find
(2) = -4. Find 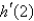 .
. 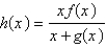
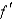 (2) = 3, g(2) = 3, and
(2) = 3, g(2) = 3, and 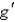 (2) = -4. Find
(2) = -4. Find 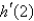 .
. 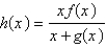

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
44
The mass of part of a wire is kilograms, where x is measured in meters from one end of the wire. Find the linear density of the wire when x = 16 m .
A) .
B)
C)
D)
E)
A) .
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
45
Differentiate the function.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
46
s(t) is the position of a body moving along a coordinate line; s(t) is measured in feet and t in seconds, where 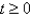 . Find the position, velocity, and speed of the body at the indicated time.
. Find the position, velocity, and speed of the body at the indicated time. 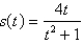 ; t = 3
; t = 3
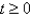 . Find the position, velocity, and speed of the body at the indicated time.
. Find the position, velocity, and speed of the body at the indicated time. 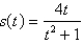 ; t = 3
; t = 3
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
47
Newton's Law of Gravitation says that the magnitude F of the force exerted by a body of mass m on a body of mass M is 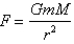 .
.
Find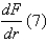 .
.
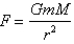 .
.Find
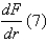 .
.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
48
Differentiate the function.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
49
A company makes computer chips from square wafers of silicon. It wants to keep the side length of a wafer very close to 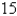 mm. The area is A(x). Find
mm. The area is A(x). Find 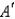 (
( 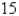 ).
).
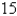 mm. The area is A(x). Find
mm. The area is A(x). Find 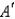 (
( 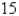 ).
).
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
50
s(t) is the position of a body moving along a coordinate line; s(t) is measured in feet and t in seconds, where 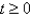 . Find the position, velocity, and speed of the body at the indicated time.
. Find the position, velocity, and speed of the body at the indicated time. 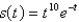 ; t = 1
; t = 1
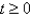 . Find the position, velocity, and speed of the body at the indicated time.
. Find the position, velocity, and speed of the body at the indicated time. 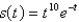 ; t = 1
; t = 1
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
51
Refer to the law of laminar flow. Consider a blood vessel with radius 0.01 cm, length 3 cm, pressure difference and viscosity =.028.
Find the velocity of the blood at radius r =
Find the velocity of the blood at radius r =

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose that f and g are functions that are differentiable at x = -3 and that f (-3) = 3, 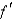 (-3) = -5, g (-3) = 3, and
(-3) = -5, g (-3) = 3, and 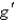 (-3) = 3. Find
(-3) = 3. Find 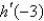 .
. 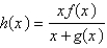
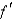 (-3) = -5, g (-3) = 3, and
(-3) = -5, g (-3) = 3, and 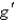 (-3) = 3. Find
(-3) = 3. Find 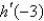 .
. 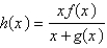

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
53
If , find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
54
Calculate y'.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
55
Find the differential of the function at the indicated number. 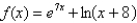 ;
; 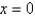
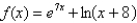 ;
; 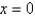

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
56
If a tank holds 5000 gallons of water, and that water can drain from the tank in 40 minutes, then Torricelli's Law gives the volume V of water remaining in the tank after t minutes as 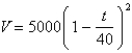 .
.
Find the rate at which water is draining from the tank after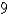 minutes.
minutes.
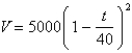 .
.Find the rate at which water is draining from the tank after
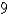 minutes.
minutes.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
57
In calm waters, the oil spilling from the ruptured hull of a grounded tanker spreads in all directions. Assuming that the polluted area is circular, determine how fast the area is increasing when the radius of the circle is 20 ft and is increasing at the rate of 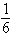 ft/sec. Round to the nearest tenth if necessary.
ft/sec. Round to the nearest tenth if necessary.
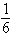 ft/sec. Round to the nearest tenth if necessary.
ft/sec. Round to the nearest tenth if necessary.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
58
Two chemicals react to form another chemical. Suppose that the amount of chemical formed in time t (in hours) is given by 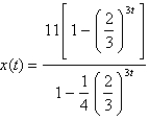 where
where 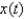 is measured in pounds.
is measured in pounds.
a. Find the rate at which the chemical is formed when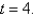 Round to two decimal places.
Round to two decimal places.
b. How many pounds of the chemical are formed eventually?
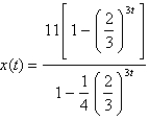 where
where 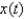 is measured in pounds.
is measured in pounds. a. Find the rate at which the chemical is formed when
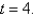 Round to two decimal places.
Round to two decimal places. b. How many pounds of the chemical are formed eventually?

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
59
s(t) is the position of a body moving along a coordinate line, where 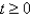 , and s(t) is measured in feet and t in seconds.
, and s(t) is measured in feet and t in seconds. 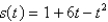
a. Determine the time(s) and the position(s) when the body is stationary.
b. When is the body moving in the positive direction? In the negative direction?
c. Sketch a schematic showing the position of the body at any time t.
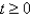 , and s(t) is measured in feet and t in seconds.
, and s(t) is measured in feet and t in seconds. 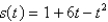
a. Determine the time(s) and the position(s) when the body is stationary.
b. When is the body moving in the positive direction? In the negative direction?
c. Sketch a schematic showing the position of the body at any time t.

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
60
The position function of a particle is given by 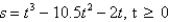 When does the particle reach a velocity of
When does the particle reach a velocity of 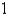 m/s?
m/s?
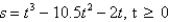 When does the particle reach a velocity of
When does the particle reach a velocity of 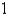 m/s?
m/s?
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
61
Find dy/dx by implicit differentiation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
62
Use logarithmic differentiation to find the derivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
63
If , find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
64
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
65
Differentiate the function. 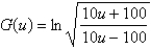
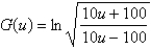

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
66
Use implicit differentiation to find an equation of the tangent line to the curve at the indicated point. y = sin xy6;
A) x =
B) y = 6x + 1
C) y = x
D) y = 1
A) x =
B) y = 6x + 1
C) y = x
D) y = 1

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
67
Find in terms of x and y.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
68
Find in terms of x and y.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
69
Find dy/dx by implicit differentiation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
70
Use logarithmic differentiation to find the derivative of the function. 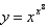
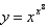

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
71
Find the tangent line to the ellipse at the point .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
72
Use logarithmic differentiation to find the derivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
73
Use implicit differentiation to find dy/dx.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
74
Differentiate the function. 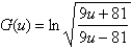
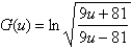

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
75
Differentiate the function. 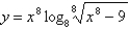
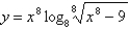

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
76
Find an equation of the tangent line to the curve 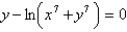 at
at 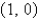 .
.
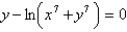 at
at 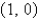 .
.
Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
77
Calculate .
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
78
Differentiate the function. 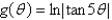
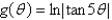

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
79
Use logarithmic differentiation to find the derivative of the function.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck
80
Use implicit differentiation to find an equation of the tangent line to the curve at the given point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 155 flashcards in this deck.
Unlock Deck
k this deck


