Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
A 20-ft ladder leaning against a wall begins to slide. How fast is the angle between the ladder and the wall changing at the instant of time when the bottom of the ladder is 13 ft from the wall and sliding away from the wall at the rate of 4 ft/sec? Round the answer to the nearest hundredth. 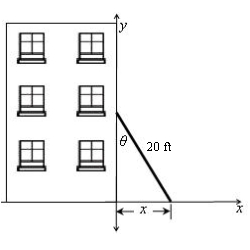 (figure not to scale)
(figure not to scale)
Free
(Short Answer)
5.0/5  (39)
(39)
Correct Answer:
0.26 rad/sec
Let .
a. Find the derivative of
b. Find the point on the graph of f where the tangent line to the curve is horizontal.
c. Sketch the graph of f and the tangent line to the curve at the point found in part (b).
d. What is the rate of change of f at this point?
Free
(Short Answer)
4.8/5  (42)
(42)
Correct Answer:
a.
b.
C. 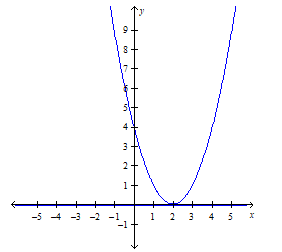
d. 0
A water trough is 20 m long and a cross-section has the shape of an isosceles trapezoid that is 20 cm wide at the bottom, 60 cm wide at the top, and has height 50 cm. If the trough is being filled with water at the rate of , how fast is the water level rising when the water is 25 cm deep? Round the result to the nearest hundredth.
(Short Answer)
4.8/5  (36)
(36)
A company makes computer chips from square wafers of silicon. It wants to keep the side length of a wafer very close to 15 mm. The area is A(x). Find ( 15 ).
(Short Answer)
4.7/5  (37)
(37)
Find an equation of the tangent line to the curve at the point
.
(Short Answer)
4.7/5  (28)
(28)
Suppose that f and g are functions that are differentiable at x = -3 and that f (-3) = 3, (-3) = -5, g (-3) = 3, and (-3) = 3. Find .
(Short Answer)
4.7/5  (43)
(43)
Use differentials to estimate the amount of paint needed to apply a coat of paint cm thick to a hemispherical dome with diameter m.
(Multiple Choice)
4.9/5  (28)
(28)
Newton's Law of Gravitation says that the magnitude F of the force exerted by a body of mass m on a body of mass M is .
Find .
(Short Answer)
4.8/5  (31)
(31)
Find the given derivative by finding the first few derivatives and observing the pattern that occurs.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)