Deck 15: Multiple Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 15: Multiple Integrals
1
Find the Jacobian of the transformation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Use cylindrical coordinates to evaluate the triple integral 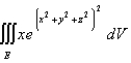 where E is the solid that lies between the sphere
where E is the solid that lies between the sphere 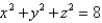 and
and 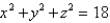 in the first octant.
in the first octant.
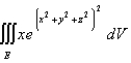 where E is the solid that lies between the sphere
where E is the solid that lies between the sphere 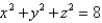 and
and 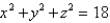 in the first octant.
in the first octant.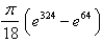
3
Use spherical coordinates. Evaluate , where is the ball with center the origin and radius .
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these
4
Identify the surface with equation 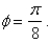
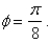

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
Use spherical coordinates to find the moment of inertia of the solid homogeneous hemisphere of radius and density 1 about a diameter of its base.
A) 205.13
B)
C) 195.22
D) 213.5
E) 198.08
A) 205.13
B)
C) 195.22
D) 213.5
E) 198.08

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the integral by making an appropriate change of variables. Round your answer to two decimal places. 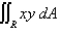 R is the parallelogram bounded by the lines
R is the parallelogram bounded by the lines 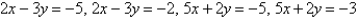 .
.
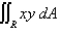 R is the parallelogram bounded by the lines
R is the parallelogram bounded by the lines 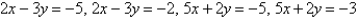 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
Use the transformation to evaluate the integral , where R is the region bounded by the ellipse .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
Identify the surface with equation 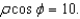
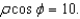

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
Find the Jacobian of the transformation. 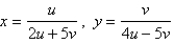
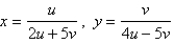

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate where and T is the region bounded by the paraboloid and the plane
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
Use spherical coordinates to find the volume of the solid that lies within the sphere 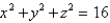 above the xy-plane and below the cone
above the xy-plane and below the cone 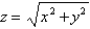 . Round the answer to two decimal places.
. Round the answer to two decimal places.
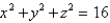 above the xy-plane and below the cone
above the xy-plane and below the cone 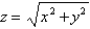 . Round the answer to two decimal places.
. Round the answer to two decimal places.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
Use the given transformation to evaluate the integral. , where R is the region in the first quadrant bounded by the lines and the hyperbolas .
A) 9.447
B) 3.296
C) 8.841
D) 4.447
E) 5.088
A) 9.447
B) 3.296
C) 8.841
D) 4.447
E) 5.088

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
Use spherical coordinate to find the volume above the cone 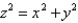 and inside sphere
and inside sphere 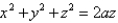 .
.
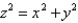 and inside sphere
and inside sphere 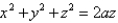 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
Find the moment of inertia with respect to a diameter of the base of a solid hemisphere of radius 3 with constant mass density function 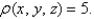
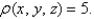

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
Use cylindrical coordinates to evaluate where T is the solid bounded by the cylinder and the planes and
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
Use the given transformation to evaluate the integral. , where R is the square with vertices (0, 0), (4, 6), (6, ), (10, 2) and
A) 208
B) 52
C) 343
D) 42
E) 312
A) 208
B) 52
C) 343
D) 42
E) 312

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
Use spherical coordinates to evaluate where B is the ball
A) 512
B) 8
C) 64
D) 1024
A) 512
B) 8
C) 64
D) 1024

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
The sketch of the solid is given below. Given , write the inequalities that describe it. 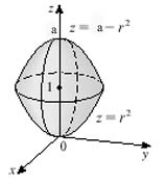
A) None of these
B)
C)
D)
E)

A) None of these
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
Identify the surface with equation 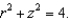
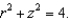

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
Find the mass of a solid hemisphere of radius 5 if the mass density at any point on the solid is directly proportional to its distance from the base of the solid.
A) k
B) k
C) k
D) k
A) k
B) k
C) k
D) k

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the integral where and with respect to x, y, and z, in that order.
A) 120
B) 620
C) 180
D) 500
A) 120
B) 620
C) 180
D) 500

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
The joint density function for a pair of random variables 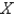 and
and 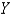 is given.
is given. 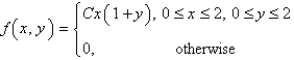 Find the value of the constant
Find the value of the constant 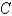 .
.
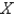 and
and 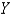 is given.
is given. 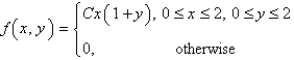 Find the value of the constant
Find the value of the constant 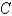 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
Express the integral as an iterated integral of the form 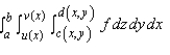 where E is the solid bounded by the surfaces
where E is the solid bounded by the surfaces 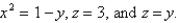
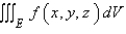
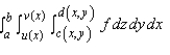 where E is the solid bounded by the surfaces
where E is the solid bounded by the surfaces 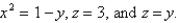
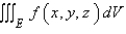

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
Find the moment of inertia about the y-axis for a cube of constant density 3 and side length 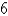 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.
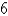 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
Use cylindrical coordinates to evaluate
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the iterated integral 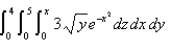
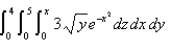

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
The joint density function for random variables 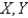 and
and 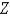 is
is 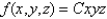 for
for 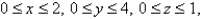 and
and 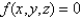 otherwise. Find the value of the constant
otherwise. Find the value of the constant 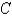 .
.
Round the answer to the nearest thousandth.
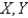 and
and 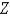 is
is 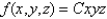 for
for 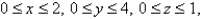 and
and 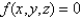 otherwise. Find the value of the constant
otherwise. Find the value of the constant 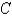 .
.Round the answer to the nearest thousandth.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
Find the center of mass of a homogeneous solid bounded by the paraboloid 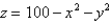 and
and 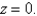
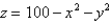 and
and 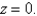

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
Calculate the iterated integral.
A) 8
B)
C)
D)
E) None of these
A) 8
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
Find the region E for which the triple integral 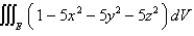 is a maximum.
is a maximum.
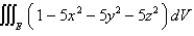 is a maximum.
is a maximum.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
Use cylindrical or spherical coordinates, whichever seems more appropriate, to evaluate where E lies above the paraboloid and below the plane .
A) 160.28
B) 175.37
C)
D) 176.38
E) 175.93
A) 160.28
B) 175.37
C)
D) 176.38
E) 175.93

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the triple integral. Round your answer to one decimal place. 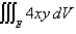
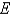 lies under the plane
lies under the plane 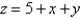 and above the region in the
and above the region in the 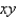 -plane bounded by the curves
-plane bounded by the curves 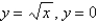 , and
, and 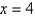 .
.
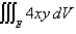
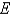 lies under the plane
lies under the plane 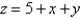 and above the region in the
and above the region in the 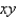 -plane bounded by the curves
-plane bounded by the curves 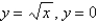 , and
, and 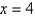 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Use a triple integral to find the volume of the solid bounded by and the planes and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
Find the mass of the solid S bounded by the paraboloid and the plane if S has constant density 3.
A) 16.25
B) 15.07
C) 24.91
D) 13.92
E) 19.63
A) 16.25
B) 15.07
C) 24.91
D) 13.92
E) 19.63

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
Use cylindrical coordinates to evaluate the triple integral where E is the solid that lies between the cylinders and above the xy-plane and below the plane .
A) 8.57
B) 0
C) 3.4
D) 9.19
E) 0.54
A) 8.57
B) 0
C) 3.4
D) 9.19
E) 0.54

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate the triple integral. Round your answer to one decimal place. 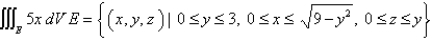
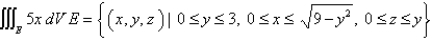

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
Use cylindrical coordinates to find the volume of the solid that the cylinder 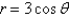 cuts out of the sphere of radius 3 centered at the origin.
cuts out of the sphere of radius 3 centered at the origin.
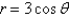 cuts out of the sphere of radius 3 centered at the origin.
cuts out of the sphere of radius 3 centered at the origin.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
Find the mass of the solid E, if E is the cube given by 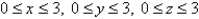 and the density function
and the density function 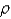 is
is 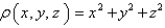 .
.
 and the density function
and the density function  is
is 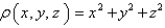 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
Express the volume of the wedge in the first octant that is cut from the cylinder 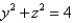 by the planes
by the planes 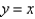 and
and 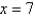 as an iterated integral with respect to
as an iterated integral with respect to 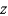 , then to
, then to 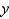 , then to
, then to 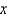 .
.
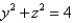 by the planes
by the planes 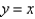 and
and 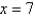 as an iterated integral with respect to
as an iterated integral with respect to 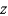 , then to
, then to 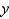 , then to
, then to 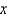 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Use cylindrical coordinates to evaluate where E is the region that lies inside the cylinder and between the planes . Round the answer to two decimal places.
A)
B) 2218.41
C) 2931.90
D) 2818.41
E) 2431.90
A)
B) 2218.41
C) 2931.90
D) 2818.41
E) 2431.90

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
Find the area of the surface. The part of the surface 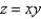 that lies within the cylinder
that lies within the cylinder 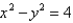 .
.
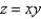 that lies within the cylinder
that lies within the cylinder 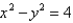 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse. Assume the vertex opposite the hypotenuse is located at , and that the sides are along the positive axes.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
Find the area of the part of the plane 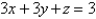 that lies in the first octant.
that lies in the first octant.
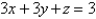 that lies in the first octant.
that lies in the first octant.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
Find the area of the surface S where S is the part of the plane 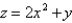 that lies above the triangular region with vertices
that lies above the triangular region with vertices 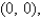
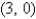 , and
, and 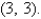
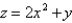 that lies above the triangular region with vertices
that lies above the triangular region with vertices 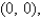
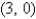 , and
, and 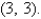

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
Sketch the solid whose volume is given by the integral 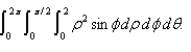 Evaluate the integral.
Evaluate the integral.
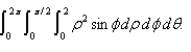 Evaluate the integral.
Evaluate the integral.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
Express the triple integral 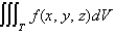 as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes
as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes 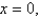
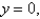
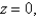 and
and 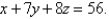
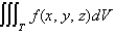 as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes
as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes 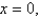
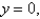
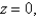 and
and 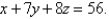

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
Find the area of the surface S where S is the part of the surface 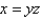 that lies inside the cylinder
that lies inside the cylinder 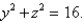
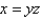 that lies inside the cylinder
that lies inside the cylinder 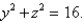

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
Find the area of the surface. The part of the surface that lies above the xy-plane.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
Find the area of the part of hyperbolic paraboloid that lies between the cylinders and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
Find the area of the surface S where S is the part of the sphere 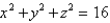 that lies to the right of the xz-plane and inside the cylinder
that lies to the right of the xz-plane and inside the cylinder 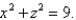
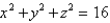 that lies to the right of the xz-plane and inside the cylinder
that lies to the right of the xz-plane and inside the cylinder 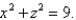

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
Find the area of the part of the plane 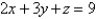 that lies inside the cylinder
that lies inside the cylinder 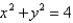 .
.
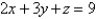 that lies inside the cylinder
that lies inside the cylinder 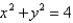 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
Find the area of the surface. The part of the sphere that lies above the plane .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
Find the area of the part of the sphere that lies inside the paraboloid .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
Sketch the solid bounded by the graphs of the equations 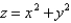 and
and 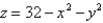 , and then use a triple integral to find the volume of the solid.
, and then use a triple integral to find the volume of the solid.
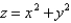 and
and 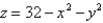 , and then use a triple integral to find the volume of the solid.
, and then use a triple integral to find the volume of the solid.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
Find the area of the surface. Round your answer to three decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
Sketch the solid whose volume is given by the iterated integral 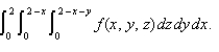
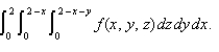

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
Find the exact area of the surface. .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
Find the area of the surface S where S is the part of the sphere 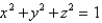 that lies inside the cylinder
that lies inside the cylinder 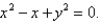
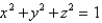 that lies inside the cylinder
that lies inside the cylinder 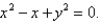

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
Set up, but do not evaluate, the iterated integral giving the mass of the solid T bounded by the cylinder 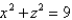 in the first octant and the plane
in the first octant and the plane 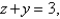 having mass density given by
having mass density given by 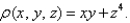
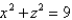 in the first octant and the plane
in the first octant and the plane 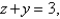 having mass density given by
having mass density given by 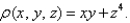

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
Describe the region whose area is given by the integral. 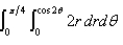
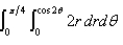

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
Find the mass and the moments of inertia 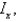
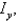 and
and 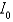 and the radii of gyration
and the radii of gyration 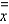 and
and 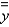 for the lamina occupying the region R, where R is the region bounded by the graphs of the equations
for the lamina occupying the region R, where R is the region bounded by the graphs of the equations 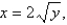
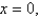 and
and 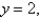 and having the mass density
and having the mass density 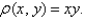
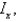
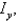 and
and 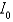 and the radii of gyration
and the radii of gyration 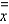 and
and 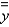 for the lamina occupying the region R, where R is the region bounded by the graphs of the equations
for the lamina occupying the region R, where R is the region bounded by the graphs of the equations 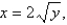
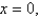 and
and 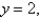 and having the mass density
and having the mass density 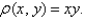

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
Find the mass and the center of mass of the lamina occupying the region R, where R is the region bounded by the graphs of 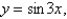
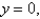
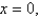 and
and 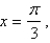 and having the mass density
and having the mass density 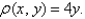
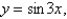
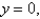
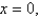 and
and 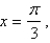 and having the mass density
and having the mass density 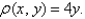

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
Use polar coordinates to find the volume of the solid inside the cylinder and the ellipsoid .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
Find the mass of the lamina that occupies the region 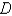 and has the given density function. Round your answer to two decimal places.
and has the given density function. Round your answer to two decimal places. 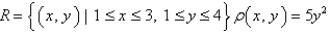
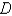 and has the given density function. Round your answer to two decimal places.
and has the given density function. Round your answer to two decimal places. 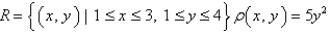

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
Find the mass and the center of mass of the lamina occupying the region R, where R is the region bounded by the graphs of the equations 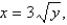
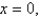 and
and 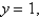 and having the mass density
and having the mass density 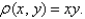
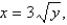
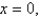 and
and 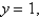 and having the mass density
and having the mass density 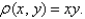

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
Use a double integral to find the area of the region R where R is bounded by the circle
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
A swimming pool is circular with a -ft diameter. The depth is constant along east-west lines and increases linearly from ft at the south end to ft at the north end. Find the volume of water in the pool.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
Find the center of mass of the system comprising masses mk located at the points Pk in a coordinate plane. Assume that mass is measured in grams and distance is measured in centimeters.
m1 = 4, m2 = 3, m3 = 2
P1(-3, -3), P2(0, 3), P3(-2, -1)
m1 = 4, m2 = 3, m3 = 2
P1(-3, -3), P2(0, 3), P3(-2, -1)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
Find the center of mass of the lamina that occupies the region D and has the given density function, if D is bounded by the parabola and the x-axis.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the integral by changing to polar coordinates. 
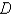 is the region bounded by the semicircle
is the region bounded by the semicircle 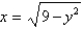 and the
and the 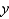 -axis.
-axis.

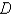 is the region bounded by the semicircle
is the region bounded by the semicircle 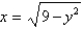 and the
and the 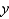 -axis.
-axis.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
An electric charge is spread over a rectangular region Find the total charge on R if the charge density at a point in R (measured in coulombs per square meter) is
A) coulombs
B) coulombs
C) coulombs
D) coulombs
A) coulombs
B) coulombs
C) coulombs
D) coulombs

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
Use polar coordinates to find the volume of the solid bounded by the paraboloid and the plane .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density
A) ,
B) ,
C) ,
D) ,
A) ,
B) ,
C) ,
D) ,

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
Evaluate the iterated integral by converting to polar coordinates. Round the answer to two decimal places. .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
A lamina occupies the part of the disk 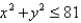 in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
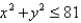 in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
Use polar coordinates to find the volume of the sphere of radius . Round to two decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
Find the center of mass of the lamina of the region shown if the density of the circular lamina is four times that of the rectangular lamina. 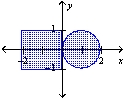


Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
Find the mass of the lamina that occupies the region D and has the given density function, if D is bounded by the parabola and the line .
A)
B)
C) 27
D)
E) None of these
A)
B)
C) 27
D)
E) None of these

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
Find the mass and the moments of inertia 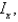
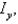 and
and 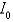 and the radii of gyration
and the radii of gyration 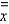 and
and 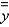 for the lamina occupying the region R, where R is the rectangular region with vertices
for the lamina occupying the region R, where R is the rectangular region with vertices 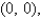
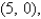
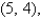 and
and 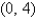 , and having uniform density
, and having uniform density 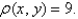
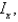
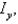 and
and 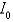 and the radii of gyration
and the radii of gyration 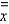 and
and 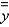 for the lamina occupying the region R, where R is the rectangular region with vertices
for the lamina occupying the region R, where R is the rectangular region with vertices 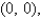
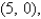
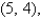 and
and 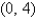 , and having uniform density
, and having uniform density 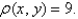

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
Use polar coordinates to find the volume of the solid under the paraboloid and above the disk .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


