Exam 15: Multiple Integrals
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use spherical coordinates to find the volume of the solid that lies within the sphere above the xy-plane and below the cone . Round the answer to two decimal places.
Free
(Short Answer)
4.8/5  (37)
(37)
Correct Answer:
39.26
Find the region E for which the triple integral is a maximum.
Free
(Short Answer)
4.7/5  (38)
(38)
Correct Answer:
Find the volume bounded by the cylinders and .
Free
(Short Answer)
4.8/5  (31)
(31)
Correct Answer:
Find the center of mass of a homogeneous solid bounded by the paraboloid and
(Short Answer)
4.9/5  (45)
(45)
The joint density function for a pair of random variables and is given. Find the value of the constant .
(Short Answer)
4.9/5  (29)
(29)
Find the area of the part of the plane that lies in the first octant.
(Short Answer)
4.7/5  (38)
(38)
Find an approximation for the integral. Use a double Riemann sum with and the sample point in the upper right corner to
approximate the double integral, where .
(Short Answer)
4.7/5  (32)
(32)
Use the Midpoint Rule for double integrals with to estimate the area of the surface. Round your answer to three decimal places.
(Short Answer)
4.9/5  (38)
(38)
Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse. Assume the vertex opposite the hypotenuse is located at , and that the sides are along the positive axes.
(Multiple Choice)
4.9/5  (30)
(30)
Find the mass and the moments of inertia and and the radii of gyration and for the lamina occupying the region R, where R is the rectangular region with vertices and , and having uniform density
(Short Answer)
4.9/5  (34)
(34)
Determine whether to use polar coordinates or rectangular coordinates to evaluate the integral , where f is a continuous function. Then write an expression for the (iterated) integral. 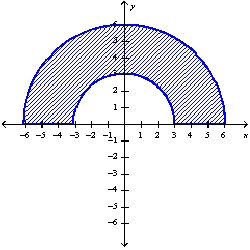
(Short Answer)
4.9/5  (26)
(26)
Use polar coordinates to find the volume of the solid under the paraboloid and above the disk .
(Multiple Choice)
5.0/5  (32)
(32)
Evaluate the integral by changing to polar coordinates. is the region bounded by the semicircle and the -axis.
(Short Answer)
4.8/5  (29)
(29)
Find the mass and the center of mass of the lamina occupying the region R, where R is the region bounded by the graphs of and and having the mass density
(Short Answer)
4.9/5  (32)
(32)
Find the mass of the lamina that occupies the region and has the given density function. Round your answer to two decimal places.
(Short Answer)
4.9/5  (44)
(44)
Calculate the double integral. Round your answer to two decimal places.
(Short Answer)
4.7/5  (42)
(42)
Showing 1 - 20 of 124
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)