Deck 13: Vector Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/93
Play
Full screen (f)
Deck 13: Vector Functions
1
Find the velocity, acceleration, and speed of an object with position function 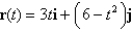 for
for 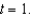 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
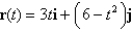 for
for 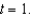 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.not answered
2
The following table gives coordinates of a particle moving through space along a smooth curve. Find the average velocity over the time interval .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
What force is required so that a particle of mass has the following position function?.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Find the acceleration of a particle with the following position function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
5
A force with magnitude N acts directly upward from the xy-plane on an object with mass kg. The object starts at the origin with initial velocity . Find its position function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
6
A projectile is fired with an initial speed of and angle of elevation . Find the range of the projectile.
A) km
B) km
C) km
D) km
E) km
A) km
B) km
C) km
D) km
E) km

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
7
Find the velocity of a particle with the given position function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
8
A particle moves with position function . Find the tangential component of the acceleration vector.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
9
A particle moves with position function 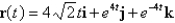 . Find the acceleration of the particle.
. Find the acceleration of the particle.
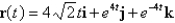 . Find the acceleration of the particle.
. Find the acceleration of the particle.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
10
Find the position vector of a particle that has the given acceleration and the given initial velocity and position. 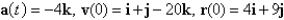
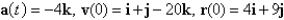

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
11
Find the scalar tangential and normal components of acceleration of a particle with position vector
A) ,
B) ,
C) ,
D) ,
A) ,
B) ,
C) ,
D) ,

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
12
Find the acceleration of a particle with the given position function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
13
A mortar shell is fired with a muzzle speed of 325 ft/sec. Find the angle of elevation of the mortar if the shell strikes a target located 1500 ft away. Round your answer to 2 decimal places.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
14
Find the speed of a particle with the given position function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
15
A particle moves with position function 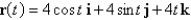 .
.
Find the normal component of the acceleration vector.
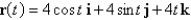 .
.Find the normal component of the acceleration vector.

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
16
Find the speed of a particle with the given position function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
17
A ball is thrown at an angle of to the ground. If the ball lands m away, what was the initial speed of the ball? Let .
A)
B) .
C) .
D)
E) .
A)
B) .
C) .
D)
E) .

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
18
Find the scalar tangential and normal components of acceleration of a particle with position vector
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
19
The position function of a particle is given by When is the speed a minimum?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
20
Find the velocity of a particle that has the given acceleration and the given initial velocity.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
21
Find the curvature of the curve .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
22
Find the scalar tangential and normal components of acceleration of a particle with position vector 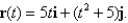
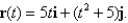

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
23
Find the curvature of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
24
Find the velocity, acceleration, and speed of an object with position function 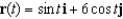 for
for 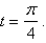 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
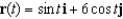 for
for 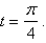 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
25
A projectile is fired from a height of 400 ft with an initial speed of 200 ft/sec and an angle of elevation of 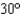 .
.
a. What are the scalar tangential and normal components of acceleration of the projectile?
b. What are the scalar tangential and normal components of acceleration of the projectile when the projectile is at its maximum height?
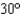 .
. a. What are the scalar tangential and normal components of acceleration of the projectile?
b. What are the scalar tangential and normal components of acceleration of the projectile when the projectile is at its maximum height?

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
26
Find the velocity and position vectors of an object with acceleration 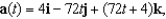 initial velocity
initial velocity 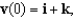 and initial position
and initial position 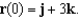
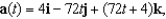 initial velocity
initial velocity 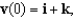 and initial position
and initial position 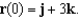

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
27
Find the length of the curve
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
28
For the curve given by , find the unit normal vector.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
29
Find the length of the curve
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
30
Find the unit tangent and unit normal vectors 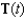 and
and 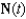 for the curve C defined by
for the curve C defined by 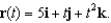
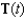 and
and 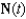 for the curve C defined by
for the curve C defined by 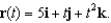

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
31
Let C be a smooth curve defined by , and let and be the unit tangent vector and unit normal vector to C corresponding to t. The plane determined by T and N is called the osculating plane. Find an equation of the osculating plane of the curve described by at
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
32
Reparametrize the curve with respect to arc length measured from the point where in the direction of increasing .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
33
Find the velocity, acceleration, and speed of an object with position vector  .
.
 .
.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
34
Find the velocity, acceleration, and speed of an object with position function 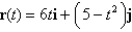 for
for 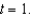 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
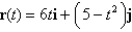 for
for 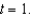 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
35
Find the unit tangent and unit normal vectors 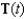 and
and 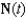 for the curve C defined by
for the curve C defined by 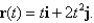 Sketch the graph of C, and show
Sketch the graph of C, and show 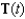 and
and 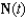 for
for 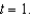
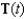 and
and 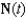 for the curve C defined by
for the curve C defined by 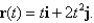 Sketch the graph of C, and show
Sketch the graph of C, and show 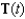 and
and 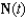 for
for 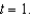

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
36
Find the velocity, acceleration, and speed of an object with position vector 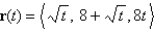 .
.
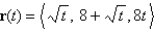 .
.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
37
A projectile is fired from ground level with an initial speed of 1100 ft/sec and an angle of elevation of 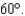
A) Find the range of the projectile.
B) What is the maximm height attained by the projectile?
C) What is the speed of the projectile at impact?
Round your answers to the nearest integer.
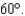
A) Find the range of the projectile.
B) What is the maximm height attained by the projectile?
C) What is the speed of the projectile at impact?
Round your answers to the nearest integer.

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
38
Find the length of the curve
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
39
Find the velocity, acceleration, and speed of an object with position function 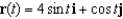 for
for 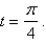 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
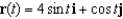 for
for 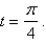 Sketch the path of the object and its velocity and acceleration vectors.
Sketch the path of the object and its velocity and acceleration vectors.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
40
Find the curvature of the curve .
A) 1
B)
C) 11
D) 0
A) 1
B)
C) 11
D) 0

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
41
Find parametric equations for the tangent line to the curve with parametric equations at the point with
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
43
Find satisfying the conditions for
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
44
The figure shows a curve given by a vector function . Choose the correct expression for . 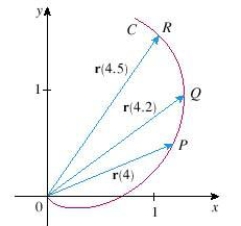
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
45
If
, find .
A)
B)
C)
D)
E)
, find .
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
46
Find equations of the normal plane to 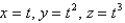 at the point (2, 4, 8).
at the point (2, 4, 8).
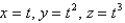 at the point (2, 4, 8).
at the point (2, 4, 8).
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
47
Find satisfying the conditions for
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
48
The torsion of a curve defined by is given by Find the torsion of the curve defined by .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
49
Find the integral
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
50
Find parametric equations for the tangent line to the curve with parametric equations at the point with
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
51
If , evaluate .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
52
Use Simpson's Rule with n = 4 to estimate the length of the arc of the curve with equations , from to . Round your answer to four decimal places.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
53
Find if and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
54
Find the arc length function 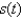 for the curve defined by
for the curve defined by 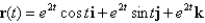 for
for 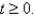 Then use this result to find a parametrization of C in terms of s.
Then use this result to find a parametrization of C in terms of s.
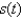 for the curve defined by
for the curve defined by 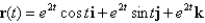 for
for 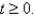 Then use this result to find a parametrization of C in terms of s.
Then use this result to find a parametrization of C in terms of s.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
55
The helix intersects the curve at the point . Find the angle of intersection.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
56
Find the unit tangent vector for at
A)
B) i + j + k
C) i j k
D)
A)
B) i + j + k
C) i j k
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
57
Find the point(s) on the graph of 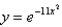 at which the curvature is zero.
at which the curvature is zero.
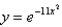 at which the curvature is zero.
at which the curvature is zero.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
58
Find the unit tangent vector .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
59
At what point on the curve is the normal plane parallel to the plane ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
60
The curvature of the curve given by the vector function is Use the formula to find the curvature of
at the point .
A)
B)
C)
D)
E)
at the point .
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
61
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
62
Given 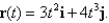
a. Find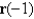 and
and 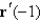 .
.
b. Sketch the curve defined by r and the vectors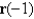 and
and 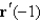 on the same set of axes.
on the same set of axes.
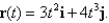
a. Find
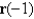 and
and 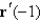 .
. b. Sketch the curve defined by r and the vectors
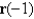 and
and 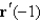 on the same set of axes.
on the same set of axes.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
63
Find the domain of the vector function .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
64
Find the unit tangent vector for the curve given by .
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
65
Find the derivative of the vector function. 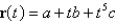
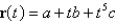

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
66
If 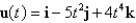 and
and 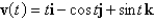 , find
, find 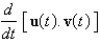 .
.
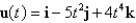 and
and 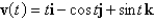 , find
, find 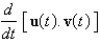 .
.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
67
Find 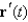 and
and 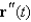 for
for 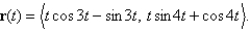
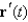 and
and 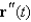 for
for 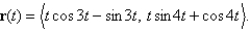

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
68
Find the point of intersection of the tangent lines to the curve 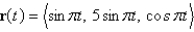 , at the points where
, at the points where 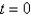 and
and 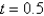 .
.
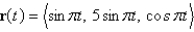 , at the points where
, at the points where 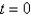 and
and 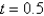 .
.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
69
The curves 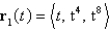 and
and 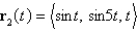 intersects at the origin. Find their angle of intersection correct to the nearest degree.
intersects at the origin. Find their angle of intersection correct to the nearest degree.
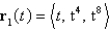 and
and 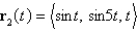 intersects at the origin. Find their angle of intersection correct to the nearest degree.
intersects at the origin. Find their angle of intersection correct to the nearest degree.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
70
Let . Find the domain of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
71
Find an expression for 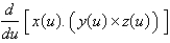 .
.
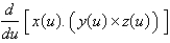 .
.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
72
Find 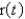 if
if 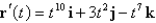 and
and 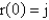 .
.
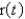 if
if 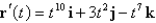 and
and 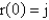 .
.
Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
73
Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
74
Find 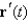 and
and 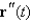 for
for 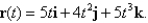
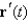 and
and 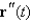 for
for 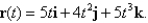

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
75
Find the domain of the vector function .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
76
Find the limit.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
77
Find the derivative 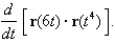
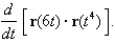

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
78
Find for the function given.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
79
Find the integral 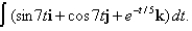
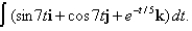

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck
80
Find 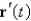 for the function given.
for the function given. 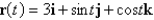
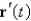 for the function given.
for the function given. 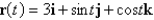

Unlock Deck
Unlock for access to all 93 flashcards in this deck.
Unlock Deck
k this deck


