Exam 13: Vector Functions
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
A force with magnitude N acts directly upward from the xy-plane on an object with mass kg. The object starts at the origin with initial velocity . Find its position function.
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
C
The curves and intersects at the origin. Find their angle of intersection correct to the nearest degree.
Free
(Short Answer)
4.8/5  (31)
(31)
Correct Answer:
Find the acceleration of a particle with the following position function.
(Multiple Choice)
4.8/5  (45)
(45)
Find a vector function describing the curve of intersection of the cylinder and the plane
(Short Answer)
5.0/5  (36)
(36)
A projectile is fired from ground level with an initial speed of 1100 ft/sec and an angle of elevation of
A) Find the range of the projectile.
B) What is the maximm height attained by the projectile?
C) What is the speed of the projectile at impact?
Round your answers to the nearest integer.
(Short Answer)
4.9/5  (37)
(37)
The figure shows a curve given by a vector function . Choose the correct expression for . 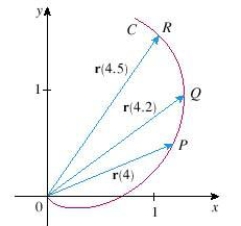
(Multiple Choice)
4.9/5  (40)
(40)
Find the unit tangent and unit normal vectors and for the curve C defined by
(Short Answer)
4.9/5  (38)
(38)
Find the arc length function for the curve defined by for Then use this result to find a parametrization of C in terms of s.
(Short Answer)
4.9/5  (39)
(39)
Use Simpson's Rule with n = 4 to estimate the length of the arc of the curve with equations , from to . Round your answer to four decimal places.
(Multiple Choice)
5.0/5  (38)
(38)
Find the velocity and position vectors of an object with acceleration initial velocity and initial position
(Short Answer)
4.8/5  (30)
(30)
The position function of a particle is given by When is the speed a minimum?
(Multiple Choice)
4.9/5  (49)
(49)
Find the speed of a particle with the given position function.
(Multiple Choice)
4.9/5  (40)
(40)
Showing 1 - 20 of 93
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)