Deck 14: One-Way Analysis of Variance- Comparing Several Means
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 14: One-Way Analysis of Variance- Comparing Several Means
1
A company runs a three-day workshop on strategies for working effectively in teams. On each day, a different strategy is presented. Forty-eight employees of the company attend the workshop. At the outset, all 48 are divided into 12 teams of four. The teams remain the same for the entire workshop. Strategies are presented in the morning. In the afternoon, the teams are presented with a series of small tasks. The number of these tasks completed successfully, using the strategy taught that morning, is recorded for each team. The mean number of tasks completed successfully by all teams each day and the standard deviation are computed. The results follow.  The researchers did an ANOVA F test of the data and obtained the following results.
The researchers did an ANOVA F test of the data and obtained the following results. 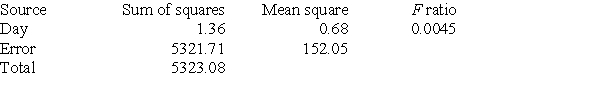 In this example, we notice that:
In this example, we notice that:
A)there is clear evidence of bias in the results. This is undoubtedly due to the lack of blinding on the part of the subjects.
B)the data show very strong evidence of a violation of the assumption that the three populations have the same standard deviation.
C)ANOVA cannot be used on these data, because the sample sizes are less than 20.
D)the assumption that the data are independent for the three days is unreasonable, because the same teams were observed each day.
 The researchers did an ANOVA F test of the data and obtained the following results.
The researchers did an ANOVA F test of the data and obtained the following results. 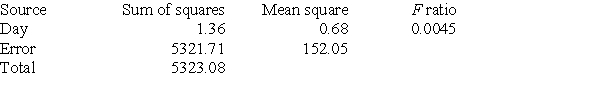 In this example, we notice that:
In this example, we notice that:A)there is clear evidence of bias in the results. This is undoubtedly due to the lack of blinding on the part of the subjects.
B)the data show very strong evidence of a violation of the assumption that the three populations have the same standard deviation.
C)ANOVA cannot be used on these data, because the sample sizes are less than 20.
D)the assumption that the data are independent for the three days is unreasonable, because the same teams were observed each day.
the assumption that the data are independent for the three days is unreasonable, because the same teams were observed each day.
2
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 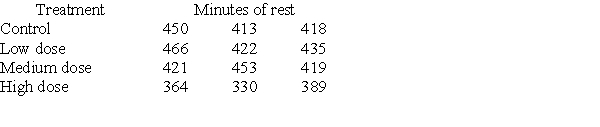 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 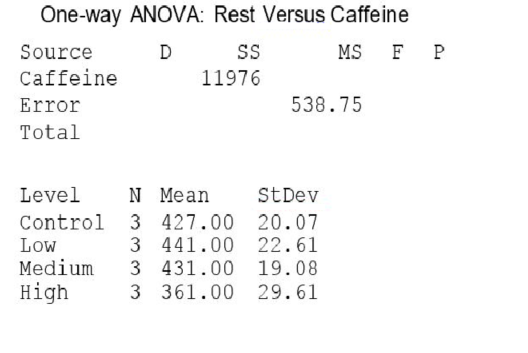 The P-value of this test is:
The P-value of this test is:
A)greater than 0.1.
B)between 0.05 and 0.1.
C)less than 0.05.
D)It is not possible to determine the P-value from the information provided.
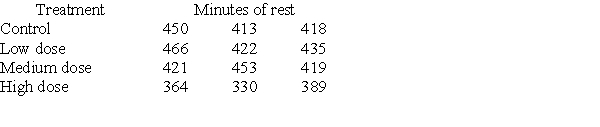 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The P-value of this test is:
The P-value of this test is:A)greater than 0.1.
B)between 0.05 and 0.1.
C)less than 0.05.
D)It is not possible to determine the P-value from the information provided.
less than 0.05.
3
A company conducted an experiment to investigate the effects of three different processes on the strength of its steel. The investigators randomly divided the production of 120 batches of steel, using 40 batches for each process. The steel was rated on a scale of 0 to 100 for its strength. The following sample means and standard deviations were obtained.  The sum of squares for groups for this experiment is given by 8952, and the sum of squares error is given by 56946. The F test is:
The sum of squares for groups for this experiment is given by 8952, and the sum of squares error is given by 56946. The F test is:
A)0.1572.
B)9.2.
C)3.03.
D)6.288.
 The sum of squares for groups for this experiment is given by 8952, and the sum of squares error is given by 56946. The F test is:
The sum of squares for groups for this experiment is given by 8952, and the sum of squares error is given by 56946. The F test is:A)0.1572.
B)9.2.
C)3.03.
D)6.288.
9.2.
4
The test statistic F used in one-way analysis of variance is:
A)a ratio of the P-values that are computed for each pairwise comparison.
B)a ratio of the variation between the sample means to the variation within the sample means.
C)a ratio of the variation within the sample means to the variation between the sample means.
D)the sum of the variations between the sample means.
A)a ratio of the P-values that are computed for each pairwise comparison.
B)a ratio of the variation between the sample means to the variation within the sample means.
C)a ratio of the variation within the sample means to the variation between the sample means.
D)the sum of the variations between the sample means.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is not a condition that must be met for one-way analysis of variance to be valid?
A)All of the populations are independent.
B)All of the populations are Normally distributed.
C)All of the populations must have the same standard deviation.
D)All of the populations must have the same variance.
A)All of the populations are independent.
B)All of the populations are Normally distributed.
C)All of the populations must have the same standard deviation.
D)All of the populations must have the same variance.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
At what age do babies learn to crawl? Does it depend on the time of the year that babies were born? Data were collected from parents who brought their babies into the University of Denver's Infant Study Center to participate in one of a number of experiments between 1988 and 1991. Parents reported the birth month and the age at which their child was first able to creep or crawl a distance of four feet within one minute. The resulting data were grouped by month of birth: January, May, and September. Crawling age is given in weeks. Assume that the data can be considered as three independent random samples (one from each of the populations composed of babies born in that particular month) and that the populations of crawling ages have Normal distributions.  An ANOVA F test was run on the data. The following shows a portion of the results.
An ANOVA F test was run on the data. The following shows a portion of the results.  The value of the ANOVA F statistic is:
The value of the ANOVA F statistic is:
A)3.15.
B)4.73.
C)6.3.
D)9.45.
 An ANOVA F test was run on the data. The following shows a portion of the results.
An ANOVA F test was run on the data. The following shows a portion of the results.  The value of the ANOVA F statistic is:
The value of the ANOVA F statistic is:A)3.15.
B)4.73.
C)6.3.
D)9.45.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
At what age do babies learn to crawl? Does it depend on the time of year that babies were born? Data were collected from parents who brought their babies into the University of Denver's Infant Study Center to participate in one of a number of experiments between 1988 and 1991. Parents reported the birth month and the age at which their child was first able to creep or crawl a distance of four feet within one minute. The resulting data were grouped by month of birth: January, May, and September. Crawling age is given in weeks. Assume that the data can be considered as three independent random samples (one from each of the populations composed of babies born in that particular month) and that the populations of crawling ages have Normal distributions.  An ANOVA F test was run on the data. The following shows a portion of the results.
An ANOVA F test was run on the data. The following shows a portion of the results.  The mean square for groups is:
The mean square for groups is:
A)5.38.
B)252.63.
C)1010.52.
D)1515.78.
 An ANOVA F test was run on the data. The following shows a portion of the results.
An ANOVA F test was run on the data. The following shows a portion of the results.  The mean square for groups is:
The mean square for groups is:A)5.38.
B)252.63.
C)1010.52.
D)1515.78.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
A company conducted an experiment to investigate the effects of three different processes on the strength of its steel. The investigators randomly divided the production of 120 batches of steel, using 40 batches for each process. The steel was rated on a scale of 0 to 100 for its strength. The following sample means and standard deviations were obtained.  The degrees of freedom for the F test are:
The degrees of freedom for the F test are:
A)3, 117.
B)3, 120.
C)2, 40.
D)2, 117.
 The degrees of freedom for the F test are:
The degrees of freedom for the F test are:A)3, 117.
B)3, 120.
C)2, 40.
D)2, 117.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
The alternative hypothesis for the one-way analysis of variance states that:
A)some of the means are statistically significant, but others are not.
B)only one mean is different from all of the others.
C)there is no difference between any of the means being considered.
D)at least one of the means is different from all of the other means.
A)some of the means are statistically significant, but others are not.
B)only one mean is different from all of the others.
C)there is no difference between any of the means being considered.
D)at least one of the means is different from all of the other means.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 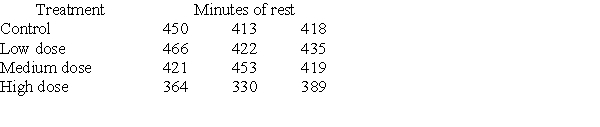 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 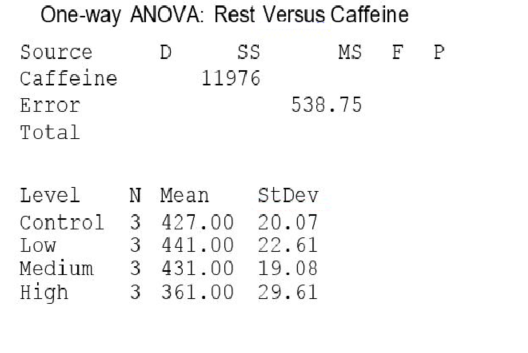 The pooled standard deviation is:
The pooled standard deviation is:
A)22.84.
B)23.21.
C)91.37.
D)2154.82.
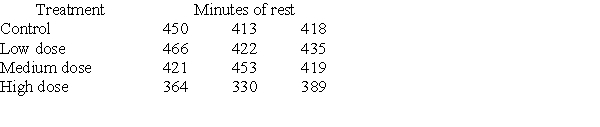 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The pooled standard deviation is:
The pooled standard deviation is:A)22.84.
B)23.21.
C)91.37.
D)2154.82.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 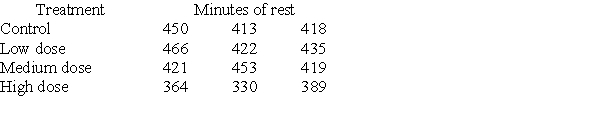 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The conclusion that you would draw from this test is:
The conclusion that you would draw from this test is:
A)accept the null hypothesis; all of the groups have the same mean.
B)fail to reject the null hypothesis; there is no evidence to suggest that the groups have different means.
C)reject the null hypothesis; all of the group means are different.
D)reject the null hypothesis; at least one of the groups has a mean that is different.
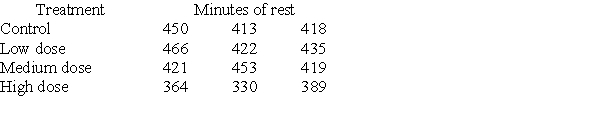 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The conclusion that you would draw from this test is:
The conclusion that you would draw from this test is:A)accept the null hypothesis; all of the groups have the same mean.
B)fail to reject the null hypothesis; there is no evidence to suggest that the groups have different means.
C)reject the null hypothesis; all of the group means are different.
D)reject the null hypothesis; at least one of the groups has a mean that is different.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
At what age do babies learn to crawl? Does it depend on the time of year that babies were born? Data were collected from parents who brought their babies into the University of Denver's Infant Study Center to participate in one of a number of experiments between 1988 and 1991. Parents reported the birth month and the age at which their child was first able to creep or crawl a distance of four feet within one minute. The resulting data were grouped by month of birth: January, May, and September. Crawling age is given in weeks. Assume that the data can be considered as three independent random samples (one from each of the populations composed of babies born in that particular month) and that the populations of crawling ages have Normal distributions.  An ANOVA F test was run on the data. The following shows a portion of the results.
An ANOVA F test was run on the data. The following shows a portion of the results.  The alternative hypothesis for the ANOVA F test is:
The alternative hypothesis for the ANOVA F test is:
A)the mean age at which babies learn to crawl is highest in September.
B)the mean age at which babies learn to crawl is different for the three birth months.
C)the mean age at which babies learn to crawl is the same for January and May.
D)None of the answer options is correct.
 An ANOVA F test was run on the data. The following shows a portion of the results.
An ANOVA F test was run on the data. The following shows a portion of the results.  The alternative hypothesis for the ANOVA F test is:
The alternative hypothesis for the ANOVA F test is:A)the mean age at which babies learn to crawl is highest in September.
B)the mean age at which babies learn to crawl is different for the three birth months.
C)the mean age at which babies learn to crawl is the same for January and May.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 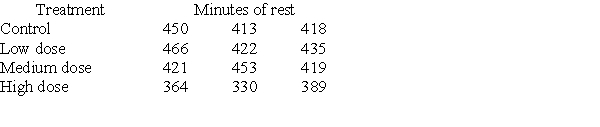 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 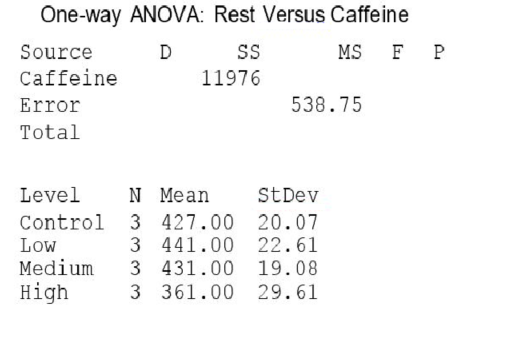 For this example, we notice that:
For this example, we notice that:
A)this is an observational study.
B)the data show evidence of a violation of the assumption that the four populations have the same standard deviation.
C)ANOVA can be used on these data because ANOVA requires the sample sizes are equal.
D)None of the answer options is correct.
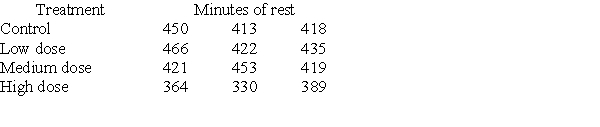 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  For this example, we notice that:
For this example, we notice that:A)this is an observational study.
B)the data show evidence of a violation of the assumption that the four populations have the same standard deviation.
C)ANOVA can be used on these data because ANOVA requires the sample sizes are equal.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 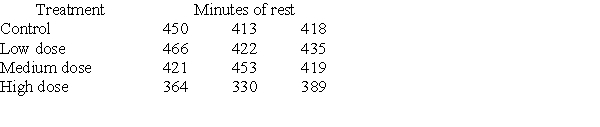 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The value of the ANOVA F statistic for testing equality of the population means of the average rest time for the four caffeine levels is:
The value of the ANOVA F statistic for testing equality of the population means of the average rest time for the four caffeine levels is:
A)2.78.
B)4.73.
C)4.82.
D)7.41.
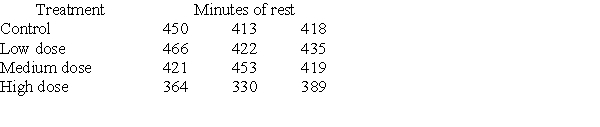 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.  The value of the ANOVA F statistic for testing equality of the population means of the average rest time for the four caffeine levels is:
The value of the ANOVA F statistic for testing equality of the population means of the average rest time for the four caffeine levels is:A)2.78.
B)4.73.
C)4.82.
D)7.41.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
A company runs a three-day workshop on strategies for working effectively in teams. On each day, a different strategy is presented. Forty-eight employees of the company attend the workshop. At the outset, all 48 are divided into 12 teams of four. The teams remain the same for the entire workshop. Strategies are presented in the morning. In the afternoon, the teams are presented with a series of small tasks. The number of these tasks completed successfully, using the strategy taught that morning, is recorded for each team. The mean number of tasks completed successfully by all teams each day and the standard deviation are computed. The results follow.  The researchers did an ANOVA F test of the data and obtained the following results.
The researchers did an ANOVA F test of the data and obtained the following results. 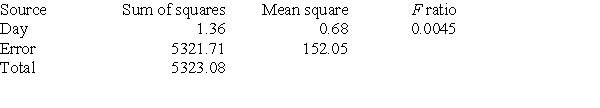 Which of the following conclusions is most reasonable?
Which of the following conclusions is most reasonable?
A)There is moderate evidence that the strategies taught are effective in increasing the number of tasks completed successfully for the first two days, but the effect appears to wear off.
B)An ANOVA F test is not appropriate for these data. Instead, the company should have done several tests to see if the number of tasks completed successfully differed for the three days. This analysis would have shown that the treatment was effective.
C)The data provide strong evidence that the mean number of tasks completed successfully differs for the three strategies taught.
D)The data appear to provide little or no evidence that the strategies taught differ in their effectiveness in helping teams complete tasks successfully.
 The researchers did an ANOVA F test of the data and obtained the following results.
The researchers did an ANOVA F test of the data and obtained the following results. 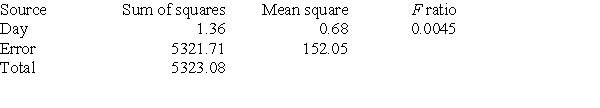 Which of the following conclusions is most reasonable?
Which of the following conclusions is most reasonable?A)There is moderate evidence that the strategies taught are effective in increasing the number of tasks completed successfully for the first two days, but the effect appears to wear off.
B)An ANOVA F test is not appropriate for these data. Instead, the company should have done several tests to see if the number of tasks completed successfully differed for the three days. This analysis would have shown that the treatment was effective.
C)The data provide strong evidence that the mean number of tasks completed successfully differs for the three strategies taught.
D)The data appear to provide little or no evidence that the strategies taught differ in their effectiveness in helping teams complete tasks successfully.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
Investigators gave caffeine to fruit flies to see if it affected their rest. The four treatments were a control, a low caffeine dose of 1 mg/ml of blood, a medium dose of 3 mg/ml of blood, and a higher caffeine dose of 5 mg/ml of blood. Twelve fruit flies were assigned at random to the four treatments, three to each treatment, and the minutes of rest measured over a 24-hour period were recorded. Assume the data that follow are four independent SRSs (one from each of the four populations of caffeine levels) and that the distribution of the yields is Normal. 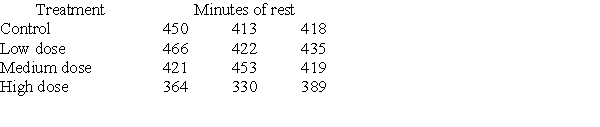 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 
The null hypothesis for the ANOVA F test is that:
A)the population mean rest is the same for all four levels of caffeine.
B)the population mean rest is increasing as the caffeine level gets larger.
C)the population mean rest is decreasing as the caffeine level gets larger.
D)the population mean rest is largest for the high level of caffeine.
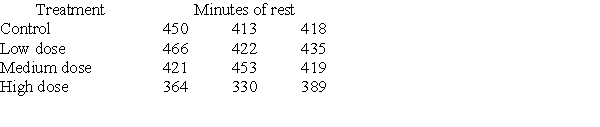 A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups.
A partial ANOVA table produced by Minitab follows, along with the means and standard deviation of the yields for the four groups. 
The null hypothesis for the ANOVA F test is that:
A)the population mean rest is the same for all four levels of caffeine.
B)the population mean rest is increasing as the caffeine level gets larger.
C)the population mean rest is decreasing as the caffeine level gets larger.
D)the population mean rest is largest for the high level of caffeine.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
A traffic engineer wanted to study the delays in traffic movement at three traffic signal locations, as measured by the number of seconds before the first car clears the intersection. The engineer selected three locations randomly from all the signals with a similar amount of traffic and number of lanes, and similar turn and signal patterns. The engineer collected the following data on eight randomly chosen days.  The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. What conditions have to hold for analysis of variance to be valid?
The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. What conditions have to hold for analysis of variance to be valid?
A)1 = 2 = 3
B)1 > 22 > 23
C)s1 = s2 = s3
D)s1 > 2s2 > 2s3
 The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. What conditions have to hold for analysis of variance to be valid?
The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. What conditions have to hold for analysis of variance to be valid?A)1 = 2 = 3
B)1 > 22 > 23
C)s1 = s2 = s3
D)s1 > 2s2 > 2s3

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
A traffic engineer wanted to study the delays in traffic movement at three traffic signal locations, as measured by the number of seconds before the first car clears the intersection. The engineer selected three locations randomly from all the signals with a similar amount of traffic and number of lanes, and similar turn and signal patterns. The engineer collected the following data on eight randomly chosen days.  The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Using technology, the engineer obtains a P-value = 0.001. This tells the engineer that:
The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Using technology, the engineer obtains a P-value = 0.001. This tells the engineer that:
A)mean delays at all three sites are different.
B)the mean delay at site 2 is the smallest and mean delay at sites 1 and 3 are the same.
C)mean delays are different for at least two sites.
D)mean delays are the same because it is rare to have different delay times.
 The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Using technology, the engineer obtains a P-value = 0.001. This tells the engineer that:
The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Using technology, the engineer obtains a P-value = 0.001. This tells the engineer that:A)mean delays at all three sites are different.
B)the mean delay at site 2 is the smallest and mean delay at sites 1 and 3 are the same.
C)mean delays are different for at least two sites.
D)mean delays are the same because it is rare to have different delay times.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following is a true statement about analysis of variance?
A)The null hypothesis test states that all population means i are the same.
B)The alternative is many-sided.
C)The F test assesses evidence for some differences among the population means i.
D)All of the answer options are correct.
A)The null hypothesis test states that all population means i are the same.
B)The alternative is many-sided.
C)The F test assesses evidence for some differences among the population means i.
D)All of the answer options are correct.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
A traffic engineer wanted to study the delays in traffic movement at three traffic signal locations, as measured by the number of seconds before the first car clears the intersection. The engineer selected three locations randomly from all the signals with a similar amount of traffic and number of lanes, and similar turn and signal patterns. The engineer collected the following data on eight randomly chosen days.  The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Which of these hypotheses should he be testing to investigate if mean delay times are the same at all locations?
The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Which of these hypotheses should he be testing to investigate if mean delay times are the same at all locations?
A)H0: 1 = 2 = 3 vs. Ha: 1 2 3
B)H0: 1 =2 = 3 vs. Ha: 2 1 = 3
C)H0: 1 = 2 = 3 vs. Ha: 1 > 3 > 3
D)None of the answer options is correct.
 The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Which of these hypotheses should he be testing to investigate if mean delay times are the same at all locations?
The engineer obtains a statistics book and, after investigating, decides that analysis of variance is the appropriate method for his problem. Which of these hypotheses should he be testing to investigate if mean delay times are the same at all locations?A)H0: 1 = 2 = 3 vs. Ha: 1 2 3
B)H0: 1 =2 = 3 vs. Ha: 2 1 = 3
C)H0: 1 = 2 = 3 vs. Ha: 1 > 3 > 3
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-2 day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. They are going to test H0: C = IG = IV versus the alternative:
A)Ha: C IG IV.
B)Ha: C IG or IG IV.
C)Ha: C IG = IV.
D)Ha: at least one of C IG or IG IV or C IV or C IG IV holds.
A)Ha: C IG IV.
B)Ha: C IG or IG IV.
C)Ha: C IG = IV.
D)Ha: at least one of C IG or IG IV or C IV or C IG IV holds.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. After consulting a statistics manual, they decided to use ANOVA for analyzing the data. Which of the following assumptions is required for the validity of this statistical procedure?
A)equality of standard deviations for the three comparison populations
B)equality of means for the three comparison populations
C)matching of the study participants in the three groups to make sure they have similar habits prior to intervention
D)nothing; the psychologists randomized and the total sample size is 30
A)equality of standard deviations for the three comparison populations
B)equality of means for the three comparison populations
C)matching of the study participants in the three groups to make sure they have similar habits prior to intervention
D)nothing; the psychologists randomized and the total sample size is 30

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week, but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. The analysis of this type of study is called:
A)a many means comparison study.
B)a multiple intervention comparison study.
C)an analysis of variance.
D)None of the answer options is correct.
A)a many means comparison study.
B)a multiple intervention comparison study.
C)an analysis of variance.
D)None of the answer options is correct.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
The one-way ANOVA is a generalization of what other statistical test?
A)ANOVA is not related to any other tests.
B)the two-sample t test for independent means
C)the paired t test for independent means
D)Levene's test for differences between variations
A)ANOVA is not related to any other tests.
B)the two-sample t test for independent means
C)the paired t test for independent means
D)Levene's test for differences between variations

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. The F-value derived from their data is F = 3.67. Therefore, we can conclude that:
A)all means are the same, since P-value > 0.10.
B)all means are different, since P-value > 0.10.
C)we do not have enough information, since we are not given the P-value.
D)the P-value is > 0.10, so there is no evidence against the null hypothesis that all means are equal.
A)all means are the same, since P-value > 0.10.
B)all means are different, since P-value > 0.10.
C)we do not have enough information, since we are not given the P-value.
D)the P-value is > 0.10, so there is no evidence against the null hypothesis that all means are equal.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. The sum of squares groups SSG = 30.494 and the sum of squares error SSE = 112.22. The F statistic value is:
A)0.272.
B)3.67.
C)1.96.
D)3.84.
A)0.272.
B)3.67.
C)1.96.
D)3.84.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. Below are 95% Tukey simultaneous confidence intervals for the pairwise comparisons of all three pairs of means.  Based on these results, which of the following statements is true?
Based on these results, which of the following statements is true?
A)Clearly, all three means are the same, since all confidence intervals include zero or nearly do so.
B)We can be 95% confident that the intervention mean is different from both the control mean and the information mean, and the control mean and the intervention mean are not different.
C)We can be sure that the intervention group is different from the control and information groups, and the information group is not different from the control group.
D)We can be confident that the intervention mean is different from the control mean and information mean, while the control mean and information mean are not different, but we do not know the confidence level.
 Based on these results, which of the following statements is true?
Based on these results, which of the following statements is true?A)Clearly, all three means are the same, since all confidence intervals include zero or nearly do so.
B)We can be 95% confident that the intervention mean is different from both the control mean and the information mean, and the control mean and the intervention mean are not different.
C)We can be sure that the intervention group is different from the control and information groups, and the information group is not different from the control group.
D)We can be confident that the intervention mean is different from the control mean and information mean, while the control mean and information mean are not different, but we do not know the confidence level.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
Many Americans complain about being sleep deprived. A team of psychologists researched the reasons for this sleep deprivation. After determining that one reason was poor time management, they devised a program to help people manage their time better. They recruited a random sample of 30 people at a major shopping center and randomly split them into three groups of size 10. Group 1 (the controls) received a logbook asking them to record the number of hours slept for a week but nothing else. Group 2 (the informed group) was shown a video to help improve time management. Group 3 (the intervention) participated in a two-day training course on improving time management. Groups 2 and 3 were also asked to keep records for one week on the number of hours slept. The psychologists were interested in learning if providing information or an intervention affects sleep time. The null hypothesis the psychologists wished to test-where C = mean sleep time for the control group, IG = mean sleep time for the information group, and IV = mean sleep time for the intervention group-is given by:
A)H0: C = IG and IG= IV.
B)H0: C = IG= IV.
C)H0: C = IG or IG = IV.
D)H0: at least of C = IG or IG = IV holds.
A)H0: C = IG and IG= IV.
B)H0: C = IG= IV.
C)H0: C = IG or IG = IV.
D)H0: at least of C = IG or IG = IV holds.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck


