Deck 7: Section 5: Applications of Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/16
Play
Full screen (f)
Deck 7: Section 5: Applications of Integration
1
A 17-foot chain that weighs 4 pounds per cubic foot hangs from a winch 17 feet above ground level. Find the work done by the winch in winding up the entire chain.
A) 346.80 ft-lb
B) 1,040.40 ft-lb
C) 867.00 ft-lb
D) 462.40 ft-lb
E) 578.00 ft-lb
A) 346.80 ft-lb
B) 1,040.40 ft-lb
C) 867.00 ft-lb
D) 462.40 ft-lb
E) 578.00 ft-lb
578.00 ft-lb
2
A quantity of gas with an initial volume of 8 cubic feet and a pressure of 1500 pounds per square foot expands to a volume of 10 cubic feet. Find the work done by the gas for the given volume and pressure. Round your answer to two decimal places.
A) 1,606.63 ft-lb
B) 4,016.58 ft-lb
C) 4,819.90 ft-lb
D) 2,677.72 ft-lb
E) 2,142.18 ft-lb
A) 1,606.63 ft-lb
B) 4,016.58 ft-lb
C) 4,819.90 ft-lb
D) 2,677.72 ft-lb
E) 2,142.18 ft-lb
2,677.72 ft-lb
3
A cylindrical gasoline tank 4 feet in diameter and 4 feet long is carried on the bank of a truck and is used to fuel tractors. The axis of the tank is horizontal. The opening on the tractor tank is 5 feet above the top of the tank in the truck. Find the work done in pumping the entire gasoline contents that weighs 42 pounds per cubic feet of the fuel tank into a tractor. (Hint: Evaluate one integral by geometric formula and the other by observing that the integrand is an odd function.)
A) 9,408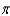 ft-lb
ft-lb
B) 4,704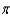 ft-lb
ft-lb
C) 2,352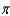 ft-lb
ft-lb
D) 25,088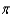 ft-lb
ft-lb
E) 20,608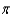 ft-lb
ft-lb
A) 9,408
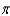 ft-lb
ft-lbB) 4,704
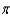 ft-lb
ft-lbC) 2,352
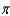 ft-lb
ft-lbD) 25,088
 ft-lb
ft-lbE) 20,608
 ft-lb
ft-lb4,704  ft-lb
ft-lb
 ft-lb
ft-lb 4
A cylindrical water tank 5 meters high with a radius of 2 meters is buried so that the top of the tank is 1 meter below ground level. How much work is done in pumping a full tank of water up to ground level? (The water weighs 9800 newtons per cubic meter.)
A) 548,800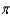 joules
joules
B) 686,000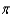 joules
joules
C) 411,600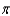 joules
joules
D) 1,234,800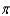 joules
joules
E) 1,029,000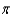 joules
joules
A) 548,800
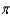 joules
joulesB) 686,000
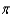 joules
joulesC) 411,600
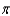 joules
joulesD) 1,234,800
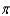 joules
joulesE) 1,029,000
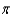 joules
joules
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
5
Determine the work done by lifting a 100 pound bag of sugar 13 feet.
A) 1,300 ft-lb
B) 13,000 ft-lb
C) 130 ft-lb
D) 2,300 ft-lb
E) 230 ft-lb
A) 1,300 ft-lb
B) 13,000 ft-lb
C) 130 ft-lb
D) 2,300 ft-lb
E) 230 ft-lb

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
6
A tank with a base of 4 feet by 3 feet and a height of 4 feet is full of water. The water weighs 62.4 pounds per cubic foot. How much work is done in pumping water out over the top edge in order to empty half of the tank. Round your answer to one decimal place. 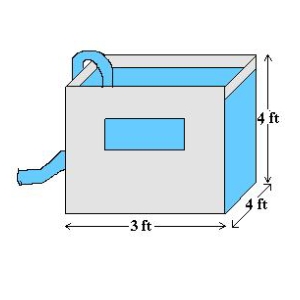
A) 499.2 ft-lb
B) 748.8 ft-lb
C) 5,990.4 ft-lb
D) 1,996.8 ft-lb
E) 1,497.6 ft-lb

A) 499.2 ft-lb
B) 748.8 ft-lb
C) 5,990.4 ft-lb
D) 1,996.8 ft-lb
E) 1,497.6 ft-lb

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
7
A force of 20 pounds stretches a spring 11 inches in an exercise machine. Find the work done in stretching the spring 2 feet from its natural position.
A)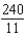 ft-lb
ft-lb
B)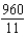 ft-lb
ft-lb
C)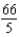 ft-lb
ft-lb
D)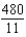 ft-lb
ft-lb
E)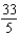 ft-lb
ft-lb
A)
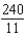 ft-lb
ft-lbB)
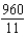 ft-lb
ft-lbC)
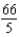 ft-lb
ft-lbD)
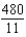 ft-lb
ft-lbE)
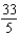 ft-lb
ft-lb
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
8
A quantity of a gas with an initial volume of 1 cubic foot and a pressure of 2000 pounds per square foot expands to a volume of 7 cubic feet. Find the work done by the gas. Round your answer to two decimal places.
A) 3,841.82 ft-lb
B) 3,891.82 ft-lb
C) 1,714.29 ft-lb
D) 1,959.18 ft-lb
E) 3,583.52 ft-lb
A) 3,841.82 ft-lb
B) 3,891.82 ft-lb
C) 1,714.29 ft-lb
D) 1,959.18 ft-lb
E) 3,583.52 ft-lb

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
9
Two electrons repel each other with a force that varies inversely as the square of the distance between them, where k is the constant of proportionality. One electron is fixed at the point 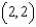 . Find the work done in moving the second electron from
. Find the work done in moving the second electron from 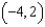 to
to 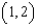 .
.
A)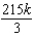 units of work
units of work
B)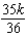 units of work
units of work
C)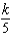 units of work
units of work
D)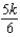 units of work
units of work
E)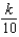 units of work
units of work
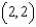 . Find the work done in moving the second electron from
. Find the work done in moving the second electron from 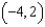 to
to 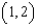 .
.A)
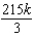 units of work
units of workB)
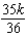 units of work
units of workC)
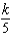 units of work
units of workD)
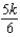 units of work
units of workE)
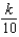 units of work
units of work
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
10
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a six-ton satellite to a height of 200 miles above earth. Assume that Earth has a radius of 4000 miles.
A)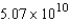 ft-lb
ft-lb
B)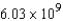 ft-lb
ft-lb
C)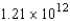 ft-lb
ft-lb
D)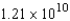 ft-lb
ft-lb
E)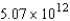 ft-lb
ft-lb
A)
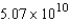 ft-lb
ft-lbB)
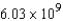 ft-lb
ft-lbC)
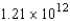 ft-lb
ft-lbD)
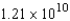 ft-lb
ft-lbE)
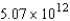 ft-lb
ft-lb
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
11
A force of 265 Newtons stretches a spring 20 centimeters. How much work is done in stretching the spring from 15 centimeters to 25 centimeters?
A) 28.5 joules
B) 31.5 joules
C) 26.5 joules
D) 21.5 joules
E) 36.5 joules
A) 28.5 joules
B) 31.5 joules
C) 26.5 joules
D) 21.5 joules
E) 36.5 joules

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
12
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a 12-ton satellite to a height of 100 miles above Earth. Assume that the Earth has a radius of 4000 miles.
A) 1,756.10 mi-ton
B) 1,170.73 mi-ton
C) 702.44 mi-ton
D) 936.59 mi-ton
E) 2,575.61 mi-ton
A) 1,756.10 mi-ton
B) 1,170.73 mi-ton
C) 702.44 mi-ton
D) 936.59 mi-ton
E) 2,575.61 mi-ton

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
13
A force of 10 pounds compresses a 21-inch spring 8 inches. How much work is done in compressing the spring from a length of 15 inches to a length of 13 inches?
A) 22.5 ft-lb
B) 19.5 ft-lb
C) 17.5 ft-lb
D) 12.5 ft-lb
E) 27.5 ft-lb
A) 22.5 ft-lb
B) 19.5 ft-lb
C) 17.5 ft-lb
D) 12.5 ft-lb
E) 27.5 ft-lb

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
14
An overhead garage door has two springs, one on each side of the door. A force of 12 pounds is required to stretch each spring 1 foot. Because of the pulley system, the springs stretch only one-half the distance the door travels. The door moves a total of 10 feet and springs are at their natural length when the door is open. Find the work done by pair of strings.
A) 150 ft-lb
B) 300 ft-lb
C) 2,400 ft-lb
D) 1,200 ft-lb
E) 600 ft-lb
A) 150 ft-lb
B) 300 ft-lb
C) 2,400 ft-lb
D) 1,200 ft-lb
E) 600 ft-lb

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
15
A lunar module weighs 16 tons on the surface of Earth. How much work is done in propelling the module from the surface of the moon to a height of 50 miles? Consider the radius of the moon to be 1100 miles and its force of gravity to be one-sixth that of Earth.
A)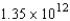 ft-lb
ft-lb
B)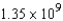 ft-lb
ft-lb
C)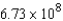 ft-lb
ft-lb
D)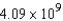 ft-lb
ft-lb
E)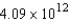 ft-lb
ft-lb
A)
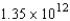 ft-lb
ft-lbB)
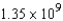 ft-lb
ft-lbC)
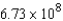 ft-lb
ft-lbD)
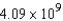 ft-lb
ft-lbE)
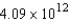 ft-lb
ft-lb
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
16
An open tank has the shape of a right circular cone. The tank is 9 feet across the top and 8 feet high. How much work is done in emptying the tank by pumping the water over the top edge? Note: The density of water is 62.4 lbs per cubic foot.
A) 6,739.20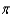 ft-lb
ft-lb
B) 4,043.52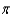 ft-lb
ft-lb
C) 5,391.36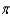 ft-lb
ft-lb
D) 10,108.80 ft-lb
ft-lb
E) 12,130.56 ft-lb
ft-lb
A) 6,739.20
 ft-lb
ft-lbB) 4,043.52
 ft-lb
ft-lbC) 5,391.36
 ft-lb
ft-lbD) 10,108.80
 ft-lb
ft-lbE) 12,130.56
 ft-lb
ft-lb
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck


