Exam 7: Section 5: Applications of Integration
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
A force of 265 Newtons stretches a spring 20 centimeters. How much work is done in stretching the spring from 15 centimeters to 25 centimeters?
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
C
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a 12-ton satellite to a height of 100 miles above Earth. Assume that the Earth has a radius of 4000 miles.
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
B
A cylindrical gasoline tank 4 feet in diameter and 4 feet long is carried on the bank of a truck and is used to fuel tractors. The axis of the tank is horizontal. The opening on the tractor tank is 5 feet above the top of the tank in the truck. Find the work done in pumping the entire gasoline contents that weighs 42 pounds per cubic feet of the fuel tank into a tractor. (Hint: Evaluate one integral by geometric formula and the other by observing that the integrand is an odd function.)
Free
(Multiple Choice)
4.8/5  (45)
(45)
Correct Answer:
B
A quantity of gas with an initial volume of 8 cubic feet and a pressure of 1500 pounds per square foot expands to a volume of 10 cubic feet. Find the work done by the gas for the given volume and pressure. Round your answer to two decimal places.
(Multiple Choice)
5.0/5  (40)
(40)
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a six-ton satellite to a height of 200 miles above earth. Assume that Earth has a radius of 4000 miles.
(Multiple Choice)
4.9/5  (42)
(42)
An overhead garage door has two springs, one on each side of the door. A force of 12 pounds is required to stretch each spring 1 foot. Because of the pulley system, the springs stretch only one-half the distance the door travels. The door moves a total of 10 feet and springs are at their natural length when the door is open. Find the work done by pair of strings.
(Multiple Choice)
4.9/5  (28)
(28)
A quantity of a gas with an initial volume of 1 cubic foot and a pressure of 2000 pounds per square foot expands to a volume of 7 cubic feet. Find the work done by the gas. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
Two electrons repel each other with a force that varies inversely as the square of the distance between them, where k is the constant of proportionality. One electron is fixed at the point 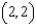 . Find the work done in moving the second electron from
. Find the work done in moving the second electron from 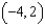 to
to 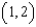 .
.
(Multiple Choice)
4.7/5  (34)
(34)
An open tank has the shape of a right circular cone. The tank is 9 feet across the top and 8 feet high. How much work is done in emptying the tank by pumping the water over the top edge? Note: The density of water is 62.4 lbs per cubic foot.
(Multiple Choice)
4.8/5  (26)
(26)
A tank with a base of 4 feet by 3 feet and a height of 4 feet is full of water. The water weighs 62.4 pounds per cubic foot. How much work is done in pumping water out over the top edge in order to empty half of the tank. Round your answer to one decimal place. 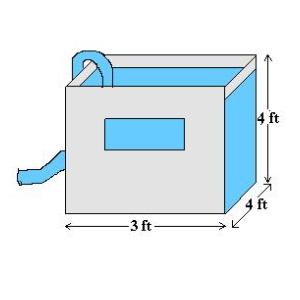
(Multiple Choice)
4.8/5  (35)
(35)
A 17-foot chain that weighs 4 pounds per cubic foot hangs from a winch 17 feet above ground level. Find the work done by the winch in winding up the entire chain.
(Multiple Choice)
4.7/5  (34)
(34)
A force of 10 pounds compresses a 21-inch spring 8 inches. How much work is done in compressing the spring from a length of 15 inches to a length of 13 inches?
(Multiple Choice)
4.8/5  (26)
(26)
A lunar module weighs 16 tons on the surface of Earth. How much work is done in propelling the module from the surface of the moon to a height of 50 miles? Consider the radius of the moon to be 1100 miles and its force of gravity to be one-sixth that of Earth.
(Multiple Choice)
4.8/5  (34)
(34)
A force of 20 pounds stretches a spring 11 inches in an exercise machine. Find the work done in stretching the spring 2 feet from its natural position.
(Multiple Choice)
4.8/5  (24)
(24)
A cylindrical water tank 5 meters high with a radius of 2 meters is buried so that the top of the tank is 1 meter below ground level. How much work is done in pumping a full tank of water up to ground level? (The water weighs 9800 newtons per cubic meter.)
(Multiple Choice)
4.8/5  (35)
(35)
Determine the work done by lifting a 100 pound bag of sugar 13 feet.
(Multiple Choice)
5.0/5  (36)
(36)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)