Deck 4: Section 6: Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/18
Play
Full screen (f)
Deck 4: Section 6: Integration
1
Use the error formula to estimate the error in approximating the integral 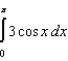 with
with  using Simpson's Rule. Round your answer to six decimal places.
using Simpson's Rule. Round your answer to six decimal places.
A) 0.007084
B) 0.141676
C) 0.004723
D) 0.003936
E) 0.002530
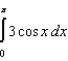 with
with  using Simpson's Rule. Round your answer to six decimal places.
using Simpson's Rule. Round your answer to six decimal places.A) 0.007084
B) 0.141676
C) 0.004723
D) 0.003936
E) 0.002530
0.003936
2
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using 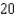 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 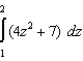
A) The Trapezoidal rule gives 16.3400 and Simpson's rule gives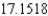 .
.
B) The Trapezoidal rule gives 16.3400 and Simpson's rule gives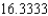 .
.
C) The Trapezoidal rule gives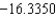 and Simpson's rule gives
and Simpson's rule gives 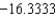 .
.
D) The Trapezoidal rule gives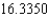 and Simpson's rule gives
and Simpson's rule gives 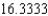 .
.
E) The Trapezoidal rule gives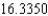 and Simpson's rule gives
and Simpson's rule gives 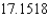 .
.
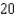 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 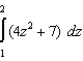
A) The Trapezoidal rule gives 16.3400 and Simpson's rule gives
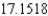 .
.B) The Trapezoidal rule gives 16.3400 and Simpson's rule gives
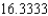 .
.C) The Trapezoidal rule gives
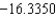 and Simpson's rule gives
and Simpson's rule gives 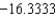 .
.D) The Trapezoidal rule gives
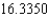 and Simpson's rule gives
and Simpson's rule gives 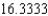 .
.E) The Trapezoidal rule gives
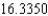 and Simpson's rule gives
and Simpson's rule gives 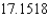 .
.The Trapezoidal rule gives 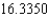 and Simpson's rule gives
and Simpson's rule gives 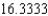 .
.
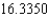 and Simpson's rule gives
and Simpson's rule gives 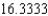 .
. 3
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using  subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 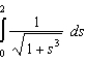
A) The Trapezoidal rule gives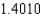 and Simpson's rule gives
and Simpson's rule gives 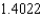 .
.
B) The Trapezoidal rule gives 1.3973 and Simpson's rule gives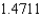 .
.
C) The Trapezoidal rule gives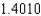 and Simpson's rule gives
and Simpson's rule gives 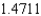 .
.
D) The Trapezoidal rule gives 1.3973 and Simpson's rule gives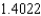 .
.
E) The Trapezoidal rule gives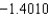 and Simpson's rule gives
and Simpson's rule gives 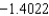 .
.
 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 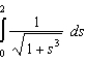
A) The Trapezoidal rule gives
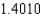 and Simpson's rule gives
and Simpson's rule gives 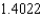 .
.B) The Trapezoidal rule gives 1.3973 and Simpson's rule gives
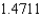 .
.C) The Trapezoidal rule gives
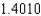 and Simpson's rule gives
and Simpson's rule gives 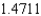 .
.D) The Trapezoidal rule gives 1.3973 and Simpson's rule gives
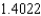 .
.E) The Trapezoidal rule gives
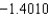 and Simpson's rule gives
and Simpson's rule gives 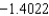 .
.The Trapezoidal rule gives 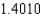 and Simpson's rule gives
and Simpson's rule gives 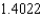 .
.
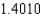 and Simpson's rule gives
and Simpson's rule gives 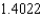 .
. 4
Use the Trapezoidal Rule to approximate the value of the definite integral 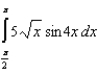 with
with  . Round your answer to four decimal places.
. Round your answer to four decimal places.
A) -8.0654
B) -4.0327
C) -2.0164
D) -1.0082
E) -0.5041
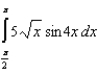 with
with  . Round your answer to four decimal places.
. Round your answer to four decimal places.A) -8.0654
B) -4.0327
C) -2.0164
D) -1.0082
E) -0.5041

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
5
Use a computer algebra system and Simpson's Rule with 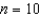 to approximate t in the integral equation
to approximate t in the integral equation 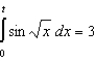 . Round your answer to three decimal places.
. Round your answer to three decimal places.
A) 3.501
B) 3.581
C) 3.901
D) 3.529
E) 3.171
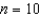 to approximate t in the integral equation
to approximate t in the integral equation 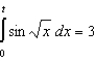 . Round your answer to three decimal places.
. Round your answer to three decimal places.A) 3.501
B) 3.581
C) 3.901
D) 3.529
E) 3.171

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
6
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using  subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 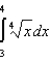
A) The Trapezoidal rule gives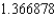 and Simpson's rule gives
and Simpson's rule gives 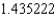 .
.
B) The Trapezoidal rule gives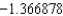 and Simpson's rule gives
and Simpson's rule gives 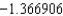 .
.
C) The Trapezoidal rule gives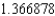 and Simpson's rule gives
and Simpson's rule gives 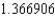 .
.
D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives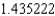 .
.
E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives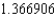 .
.
 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 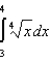
A) The Trapezoidal rule gives
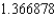 and Simpson's rule gives
and Simpson's rule gives 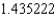 .
.B) The Trapezoidal rule gives
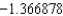 and Simpson's rule gives
and Simpson's rule gives 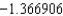 .
.C) The Trapezoidal rule gives
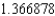 and Simpson's rule gives
and Simpson's rule gives 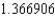 .
.D) The Trapezoidal rule gives 1.366795 and Simpson's rule gives
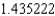 .
.E) The Trapezoidal rule gives 1.366795 and Simpson's rule gives
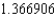 .
.
Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
7
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using  subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 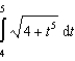
A) The Trapezoidal rule gives 43.377044 and Simpson's rule gives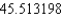 .
.
B) The Trapezoidal rule gives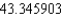 and Simpson's rule gives
and Simpson's rule gives 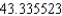 .
.
C) The Trapezoidal rule gives 43.377044 and Simpson's rule gives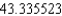 .
.
D) The Trapezoidal rule gives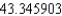 and Simpson's rule gives
and Simpson's rule gives 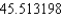 .
.
E) The Trapezoidal rule gives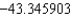 and Simpson's rule gives
and Simpson's rule gives 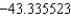 .
.
 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 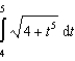
A) The Trapezoidal rule gives 43.377044 and Simpson's rule gives
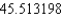 .
.B) The Trapezoidal rule gives
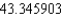 and Simpson's rule gives
and Simpson's rule gives 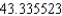 .
.C) The Trapezoidal rule gives 43.377044 and Simpson's rule gives
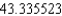 .
.D) The Trapezoidal rule gives
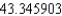 and Simpson's rule gives
and Simpson's rule gives 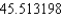 .
.E) The Trapezoidal rule gives
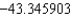 and Simpson's rule gives
and Simpson's rule gives 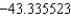 .
.
Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
8
Find the smallest n such that the error estimate in the approximation of the definite integral 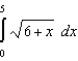 is less than 0.00001 using Simpson's Rule.
is less than 0.00001 using Simpson's Rule.
A) 10
B) 16
C) 6
D) 8
E) 13
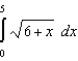 is less than 0.00001 using Simpson's Rule.
is less than 0.00001 using Simpson's Rule.A) 10
B) 16
C) 6
D) 8
E) 13

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
9
Use Simpson's Rule to approximate the value of the definite integral 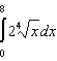 with
with  . Round your answer to four decimal places.
. Round your answer to four decimal places.
A)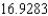
B)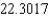
C)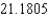
D)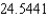
E)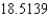
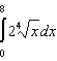 with
with  . Round your answer to four decimal places.
. Round your answer to four decimal places.A)
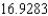
B)
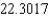
C)
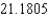
D)
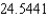
E)
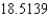

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
10
Use Simpson's Rule with 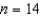 to approximate
to approximate 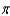 using the equation
using the equation 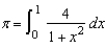 . Round your answer to five decimal places.
. Round your answer to five decimal places.
A) 3.14159
B) 3.13595
C) 3.14723
D) 3.14381
E) 3.13937
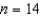 to approximate
to approximate 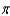 using the equation
using the equation 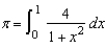 . Round your answer to five decimal places.
. Round your answer to five decimal places.A) 3.14159
B) 3.13595
C) 3.14723
D) 3.14381
E) 3.13937

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
11
Apply the Trapezoidal Rule and Simpson's Rule to approximate the value of the definite integral using 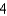 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 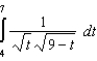
A) The Trapezoidal rule gives 0.7100 and Simpson's rule gives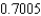 .
.
B) The Trapezoidal rule gives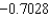 and Simpson's rule gives
and Simpson's rule gives 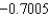 .
.
C) The Trapezoidal rule gives 0.7100 and Simpson's rule gives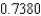 .
.
D) The Trapezoidal rule gives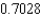 and Simpson's rule gives
and Simpson's rule gives 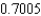 .
.
E) The Trapezoidal rule gives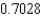 and Simpson's rule gives
and Simpson's rule gives 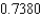 .
.
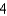 subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral.
subintervals. Round your answer to six decimal places and compare the result with the exact value of the definite integral. 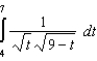
A) The Trapezoidal rule gives 0.7100 and Simpson's rule gives
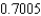 .
.B) The Trapezoidal rule gives
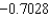 and Simpson's rule gives
and Simpson's rule gives 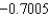 .
.C) The Trapezoidal rule gives 0.7100 and Simpson's rule gives
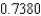 .
.D) The Trapezoidal rule gives
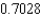 and Simpson's rule gives
and Simpson's rule gives 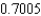 .
.E) The Trapezoidal rule gives
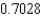 and Simpson's rule gives
and Simpson's rule gives 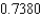 .
.
Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
12
Find the smallest n such that the error estimate in the approximation of the definite integral 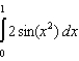 is less than 0.00001 using the Trapezoidal Rule. Use a graphing utility to estimate the maximum of the absolute value of the second derivative.
is less than 0.00001 using the Trapezoidal Rule. Use a graphing utility to estimate the maximum of the absolute value of the second derivative.
A) 208
B) 189
C) 196
D) 201
E) 188
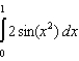 is less than 0.00001 using the Trapezoidal Rule. Use a graphing utility to estimate the maximum of the absolute value of the second derivative.
is less than 0.00001 using the Trapezoidal Rule. Use a graphing utility to estimate the maximum of the absolute value of the second derivative.A) 208
B) 189
C) 196
D) 201
E) 188

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
13
Find the smallest n such that the error estimate in the approximation of the definite integral 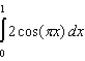 is less than 0.00001 using Simpson's Rule.
is less than 0.00001 using Simpson's Rule.
A) 48
B) 8
C) 11
D) 14
E) 19
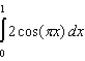 is less than 0.00001 using Simpson's Rule.
is less than 0.00001 using Simpson's Rule.A) 48
B) 8
C) 11
D) 14
E) 19

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
14
Use the Trapezoid Rule to approximate the value of the definite integral 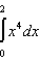 wth
wth  . Round your answer to four decimal places.
. Round your answer to four decimal places.
A)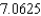
B)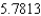
C)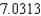
D)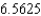
E)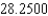
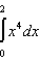 wth
wth  . Round your answer to four decimal places.
. Round your answer to four decimal places.A)
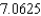
B)
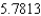
C)
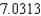
D)
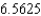
E)

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
15
Use Simpson's Rule to approximate the value of the definite integral 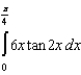 with
with  . Round your answer to four decimal places.
. Round your answer to four decimal places.
A) 2.9784
B) 3.0627
C) 8.0100
D) 10.6800
E) 2.6700
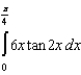 with
with  . Round your answer to four decimal places.
. Round your answer to four decimal places.A) 2.9784
B) 3.0627
C) 8.0100
D) 10.6800
E) 2.6700

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
16
Estimate the error in using (a) the Trapezoidal Rule and (b) Simpson's Rule with  when approximating the following integral.
when approximating the following integral. 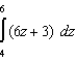
A) The error for the Trapezoidal Rule is 0.0051 and for Simpson's Rule it is 0.0013.
B) The error for the Trapezoidal Rule is 0.0000 and for Simpson's Rule it is 0.0200.
C) The error for the Trapezoidal Rule is 0.0204 and for Simpson's Rule it is 0.0200.
D) The error for the Trapezoidal Rule is 0.0204 and for Simpson's Rule it is 0.0000.
E) The error for the Trapezoidal Rule is 0.0000 and for Simpson's Rule it is 0.0000.
 when approximating the following integral.
when approximating the following integral. 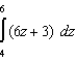
A) The error for the Trapezoidal Rule is 0.0051 and for Simpson's Rule it is 0.0013.
B) The error for the Trapezoidal Rule is 0.0000 and for Simpson's Rule it is 0.0200.
C) The error for the Trapezoidal Rule is 0.0204 and for Simpson's Rule it is 0.0200.
D) The error for the Trapezoidal Rule is 0.0204 and for Simpson's Rule it is 0.0000.
E) The error for the Trapezoidal Rule is 0.0000 and for Simpson's Rule it is 0.0000.

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
17
Use the error formula to estimate the error in approximating the integral 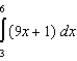 with
with  using Trapezoidal Rule.
using Trapezoidal Rule.
A) 3
B) 1
C) 6
D) 0
E) 9
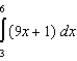 with
with  using Trapezoidal Rule.
using Trapezoidal Rule.A) 3
B) 1
C) 6
D) 0
E) 9

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck
18
Find the smallest n such that the error estimate from the error formula in the approximation of the definite integral 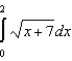 is less than 0.00001 using the Trapezoidal Rule.
is less than 0.00001 using the Trapezoidal Rule.
A) 49
B) 26
C) 73
D) 30
E) 15
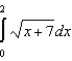 is less than 0.00001 using the Trapezoidal Rule.
is less than 0.00001 using the Trapezoidal Rule.A) 49
B) 26
C) 73
D) 30
E) 15

Unlock Deck
Unlock for access to all 18 flashcards in this deck.
Unlock Deck
k this deck


