Deck 3: Section 7: Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/16
Play
Full screen (f)
Deck 3: Section 7: Differentiation
1
A point is moving along the graph of the function 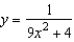 such that
such that 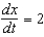 centimeters per second. Find
centimeters per second. Find 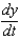 when x =
when x = 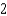 .
.
A)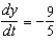
B)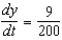
C)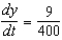
D)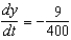
E)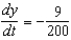
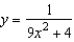 such that
such that 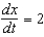 centimeters per second. Find
centimeters per second. Find 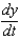 when x =
when x = 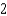 .
.A)
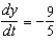
B)
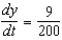
C)
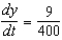
D)
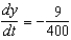
E)
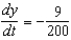
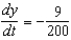
2
A man 6 feet tall walks at a rate of 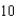 feet per second away from a light that is 15 feet above the ground (see figure). When he is
feet per second away from a light that is 15 feet above the ground (see figure). When he is 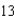 feet from the base of the light, at what rate is the tip of his shadow moving?
feet from the base of the light, at what rate is the tip of his shadow moving? 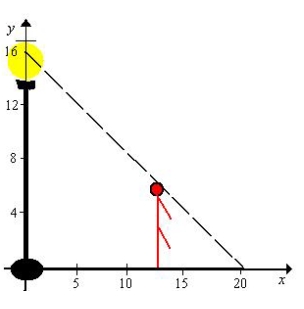
A)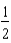 ft/sec
ft/sec
B)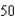 ft/sec
ft/sec
C)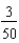 ft/sec
ft/sec
D)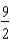 ft/sec
ft/sec
E)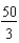 ft/sec
ft/sec
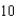 feet per second away from a light that is 15 feet above the ground (see figure). When he is
feet per second away from a light that is 15 feet above the ground (see figure). When he is 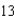 feet from the base of the light, at what rate is the tip of his shadow moving?
feet from the base of the light, at what rate is the tip of his shadow moving? 
A)
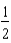 ft/sec
ft/secB)
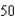 ft/sec
ft/secC)
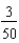 ft/sec
ft/secD)
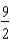 ft/sec
ft/secE)
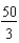 ft/sec
ft/sec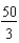 ft/sec
ft/sec 3
A ladder 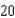 feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of
feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of 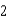 feet per second. Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is
feet per second. Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 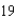 feet from the wall. Round your answer to three decimal places.
feet from the wall. Round your answer to three decimal places. 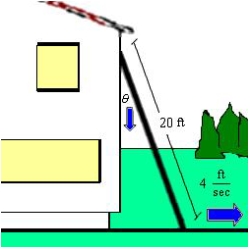
A)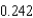 rad/sec
rad/sec
B)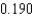 rad/sec
rad/sec
C)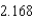 rad/sec
rad/sec
D)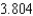 rad/sec
rad/sec
E)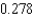 rad/sec
rad/sec
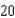 feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of
feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of  feet per second. Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is
feet per second. Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 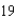 feet from the wall. Round your answer to three decimal places.
feet from the wall. Round your answer to three decimal places. 
A)
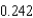 rad/sec
rad/secB)
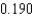 rad/sec
rad/secC)
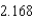 rad/sec
rad/secD)
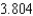 rad/sec
rad/secE)
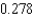 rad/sec
rad/sec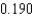 rad/sec
rad/sec 4
Find the rate of change of the distance 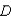 between the origin and a moving point on the graph of
between the origin and a moving point on the graph of 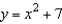 if
if 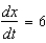 centimeters per second.
centimeters per second.
A)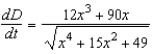
B)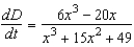
C)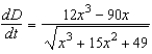
D)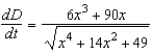
E)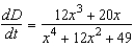
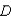 between the origin and a moving point on the graph of
between the origin and a moving point on the graph of 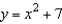 if
if 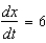 centimeters per second.
centimeters per second.A)
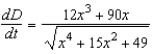
B)
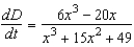
C)
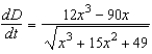
D)
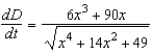
E)
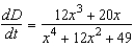

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
5
A conical tank (with vertex down) is 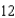 feet across the top and
feet across the top and 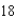 feet deep. If water is flowing into the tank at a rate of
feet deep. If water is flowing into the tank at a rate of 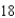 cubic feet per minute, find the rate of change of the depth of the water when the water is
cubic feet per minute, find the rate of change of the depth of the water when the water is 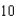 feet deep.
feet deep.
A)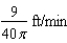
B)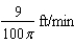
C)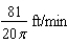
D)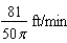
E)
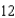 feet across the top and
feet across the top and 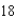 feet deep. If water is flowing into the tank at a rate of
feet deep. If water is flowing into the tank at a rate of 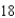 cubic feet per minute, find the rate of change of the depth of the water when the water is
cubic feet per minute, find the rate of change of the depth of the water when the water is 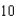 feet deep.
feet deep.A)
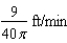
B)
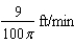
C)
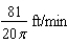
D)
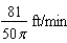
E)


Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
6
All edges of a cube are expanding at a rate of 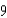 centimeters per second. How fast is the volume changing when each edge is
centimeters per second. How fast is the volume changing when each edge is 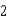 centimeters?
centimeters?
A)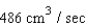
B)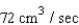
C)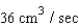
D)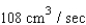
E)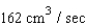
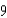 centimeters per second. How fast is the volume changing when each edge is
centimeters per second. How fast is the volume changing when each edge is 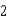 centimeters?
centimeters?A)
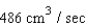
B)
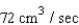
C)
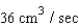
D)
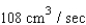
E)
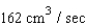

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
7
Assume that x and y are both differentiable functions of t. Find 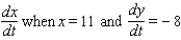 for the equation
for the equation 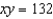 .
.
A)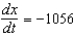
B)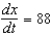
C)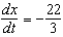
D)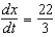
E)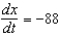
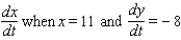 for the equation
for the equation 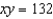 .
.A)
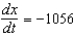
B)
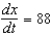
C)
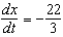
D)
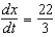
E)
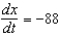

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
8
An airplane is flying in still air with an airspeed of 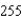 miles per hour. If it is climbing at an angle of
miles per hour. If it is climbing at an angle of 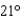 , find the rate at which it is gaining altitude. Round your answer to four decimal places.
, find the rate at which it is gaining altitude. Round your answer to four decimal places.
A)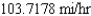
B)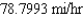
C)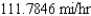
D)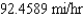
E)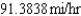
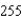 miles per hour. If it is climbing at an angle of
miles per hour. If it is climbing at an angle of 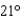 , find the rate at which it is gaining altitude. Round your answer to four decimal places.
, find the rate at which it is gaining altitude. Round your answer to four decimal places.A)
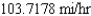
B)
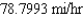
C)
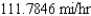
D)
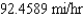
E)
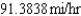

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
9
Assume that x and y are both differentiable functions of t . Find 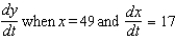 for the equation
for the equation 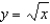 .
.
A)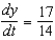
B)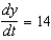
C)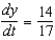
D)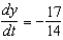
E)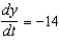
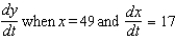 for the equation
for the equation 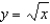 .
.A)
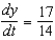
B)
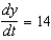
C)
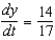
D)
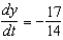
E)
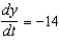

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
10
A ladder 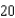 feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of
feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of 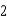 feet per second. How fast is the top of the ladder moving down the wall when its base is
feet per second. How fast is the top of the ladder moving down the wall when its base is 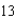 feet from the wall? Round your answer to two decimal places.
feet from the wall? Round your answer to two decimal places. 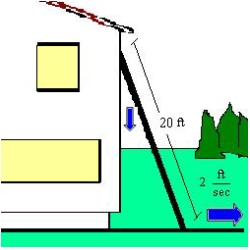
A)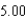 ft/sec
ft/sec
B)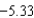 ft/sec
ft/sec
C)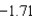 ft/sec
ft/sec
D)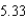 ft/sec
ft/sec
E)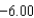 ft/sec
ft/sec
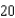 feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of
feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of 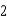 feet per second. How fast is the top of the ladder moving down the wall when its base is
feet per second. How fast is the top of the ladder moving down the wall when its base is 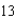 feet from the wall? Round your answer to two decimal places.
feet from the wall? Round your answer to two decimal places. 
A)
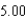 ft/sec
ft/secB)
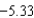 ft/sec
ft/secC)
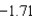 ft/sec
ft/secD)
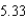 ft/sec
ft/secE)
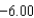 ft/sec
ft/sec
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
11
The radius, r, of a circle is decreasing at a rate of 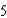 centimeters per minute. Find the rate of change of area, A, when the radius is
centimeters per minute. Find the rate of change of area, A, when the radius is 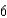 .
.
A)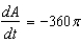 sq cm/min
sq cm/min
B)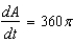 sq cm/min
sq cm/min
C)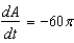 sq cm/min
sq cm/min
D)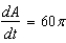 sq cm/min
sq cm/min
E)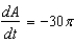 sq cm/min
sq cm/min
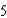 centimeters per minute. Find the rate of change of area, A, when the radius is
centimeters per minute. Find the rate of change of area, A, when the radius is 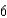 .
.A)
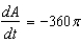 sq cm/min
sq cm/minB)
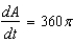 sq cm/min
sq cm/minC)
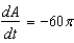 sq cm/min
sq cm/minD)
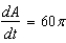 sq cm/min
sq cm/minE)
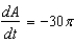 sq cm/min
sq cm/min
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
12
The radius r of a sphere is increasing at a rate of 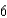 inches per minute. Find the rate of change of the volume when r =
inches per minute. Find the rate of change of the volume when r = 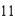 inches.
inches.
A)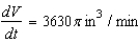
B)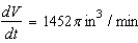
C)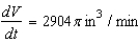
D)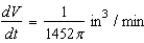
E)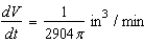
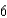 inches per minute. Find the rate of change of the volume when r =
inches per minute. Find the rate of change of the volume when r = 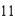 inches.
inches.A)
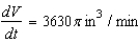
B)
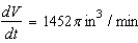
C)
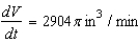
D)
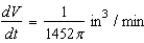
E)
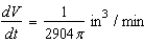

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
13
A point is moving along the graph of the function 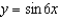 such that
such that 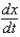 =
= 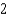 centimeters per second. Find
centimeters per second. Find 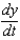 when
when 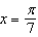 .
.
A)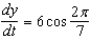
B)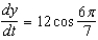
C)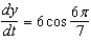
D)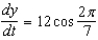
E)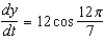
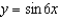 such that
such that 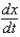 =
= 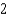 centimeters per second. Find
centimeters per second. Find 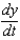 when
when 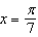 .
.A)
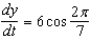
B)
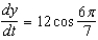
C)
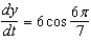
D)
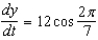
E)
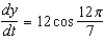

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
14
A ladder 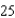 feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of
feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of 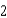 feet per second. Consider the triangle formed by the side of the house, the ladder, and the ground. Find the rate at which the area of the triangle is changed when the base of the ladder is
feet per second. Consider the triangle formed by the side of the house, the ladder, and the ground. Find the rate at which the area of the triangle is changed when the base of the ladder is 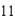 feet from the wall. Round your answer to two decimal places.
feet from the wall. Round your answer to two decimal places. 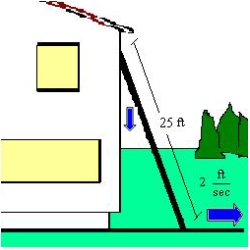
A)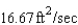
B)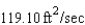
C)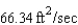
D)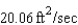
E)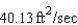
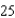 feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of
feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of 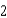 feet per second. Consider the triangle formed by the side of the house, the ladder, and the ground. Find the rate at which the area of the triangle is changed when the base of the ladder is
feet per second. Consider the triangle formed by the side of the house, the ladder, and the ground. Find the rate at which the area of the triangle is changed when the base of the ladder is 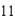 feet from the wall. Round your answer to two decimal places.
feet from the wall. Round your answer to two decimal places. 
A)
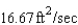
B)
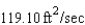
C)
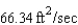
D)
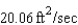
E)
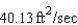

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
15
A man 6 feet tall walks at a rate of 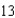 feet per second away from a light that is 15 feet above the ground (see figure). When he is
feet per second away from a light that is 15 feet above the ground (see figure). When he is 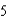 feet from the base of the light, at what rate is the length of his shadow changing?
feet from the base of the light, at what rate is the length of his shadow changing? 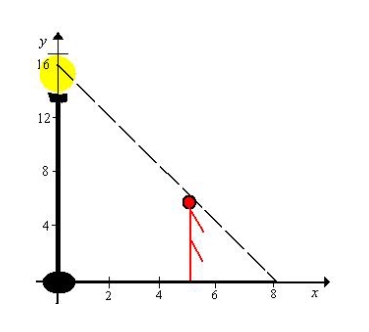
A)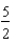 ft/sec
ft/sec
B)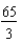 ft/sec
ft/sec
C)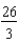 ft/sec
ft/sec
D)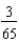 ft/sec
ft/sec
E)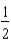 ft/sec
ft/sec
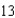 feet per second away from a light that is 15 feet above the ground (see figure). When he is
feet per second away from a light that is 15 feet above the ground (see figure). When he is 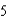 feet from the base of the light, at what rate is the length of his shadow changing?
feet from the base of the light, at what rate is the length of his shadow changing? 
A)
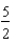 ft/sec
ft/secB)
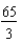 ft/sec
ft/secC)
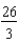 ft/sec
ft/secD)
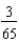 ft/sec
ft/secE)
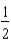 ft/sec
ft/sec
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
16
A spherical balloon is inflated with gas at the rate of 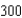 cubic centimeters per minute. How fast is the radius of the balloon increasing at the instant the radius is
cubic centimeters per minute. How fast is the radius of the balloon increasing at the instant the radius is 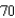 centimeters?
centimeters?
A)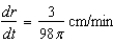
B)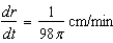
C)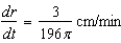
D)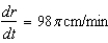
E)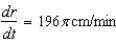
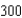 cubic centimeters per minute. How fast is the radius of the balloon increasing at the instant the radius is
cubic centimeters per minute. How fast is the radius of the balloon increasing at the instant the radius is 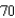 centimeters?
centimeters?A)
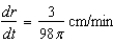
B)
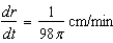
C)
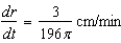
D)
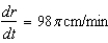
E)
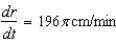

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck


