Deck 1: Section 4: Preparation for Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/16
Play
Full screen (f)
Deck 1: Section 4: Preparation for Calculus
1
Students in a lab measured the breaking strength S (in pounds) of wood 2 inches thick, x inches high, and 12 inches long. The results are shown in the table below. Use the regression capabilities of a graphing utility to fit a quadratic model to the data. Round the numerical values in your answer to two decimal places, where applicable. 
A)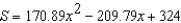
B)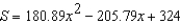
C)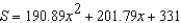
D)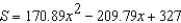
E)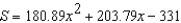

A)
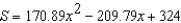
B)
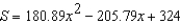
C)
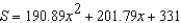
D)
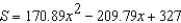
E)
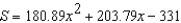
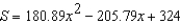
2
Students in a lab measured the breaking strength S (in pounds) of wood 2 inches thick, x inches high, and 12 inches long. The results are shown in the table below. Use a graphing utility to plot the data and graph the quadratic model. 
A)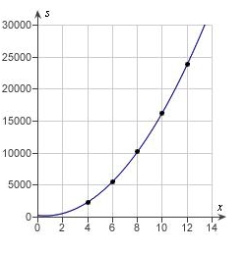
B)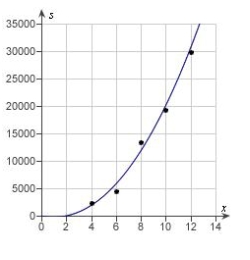
C)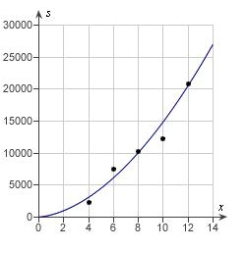
D)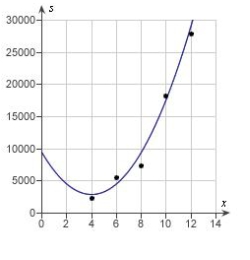
E)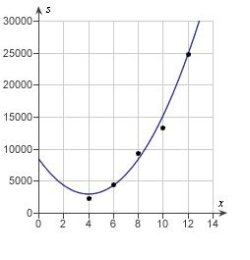

A)

B)

C)

D)

E)


3
In an experiment, students measured the speed s (in meters per second) of a falling object t seconds after it was released. The results are shown in the table below. Use the model 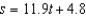 to estimate the speed of the object after
to estimate the speed of the object after 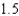 seconds. Round your answer to two decimal places.
seconds. Round your answer to two decimal places. 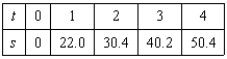
A) 21.05 meters/second
B) 20.95 meters/second
C) 24.25 meters/second
D) 23.55 meters/second
E) 22.65 meters/second
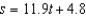 to estimate the speed of the object after
to estimate the speed of the object after 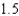 seconds. Round your answer to two decimal places.
seconds. Round your answer to two decimal places. 
A) 21.05 meters/second
B) 20.95 meters/second
C) 24.25 meters/second
D) 23.55 meters/second
E) 22.65 meters/second
22.65 meters/second
4
A V8 car engine is coupled to a dynamometer and the horsepower y is measured at different engine speeds x (in thousands of revolutions per minute). The results are shown in the table below. Use a graphing utility to plot the data and graph the cubic model. 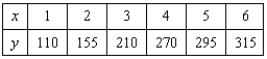
A)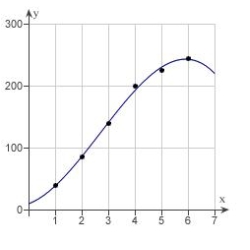
B)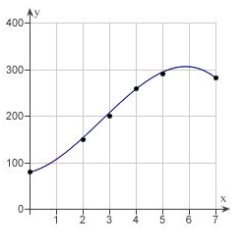
C)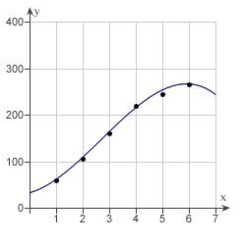
D)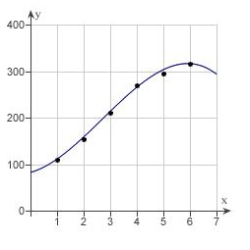
E)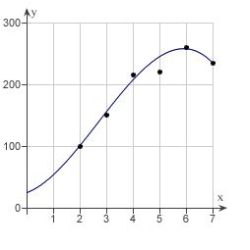

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
5
Each ordered pair gives the exposure index x of a carcinogenic substance and the cancer mortality y per 100,000 people in the population. Use the model 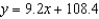 to approximate y if
to approximate y if 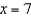 . Round your answer to one decimal place.
. Round your answer to one decimal place. 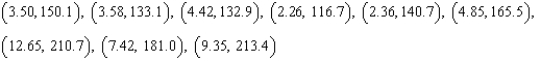
A) 168.2
B) 163.6
C) 182.0
D) 172.8
E) 177.4
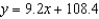 to approximate y if
to approximate y if 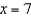 . Round your answer to one decimal place.
. Round your answer to one decimal place. 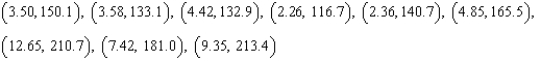
A) 168.2
B) 163.6
C) 182.0
D) 172.8
E) 177.4

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
6
Hooke's Law states that the force F required to compress or stretch a spring (within its elastic limits) is proportional to the distance d that the spring is compressed or stretched from its original length. That is, 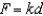 where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use a graphing utility to plot the data and graph the linear model.
where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use a graphing utility to plot the data and graph the linear model. 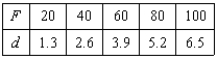
A)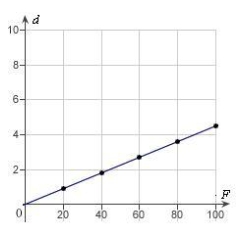
B)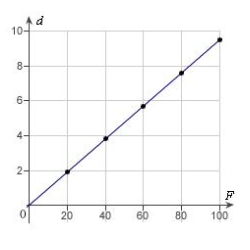
C)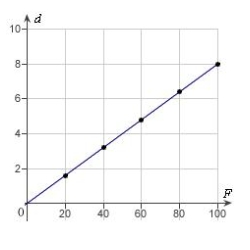
D)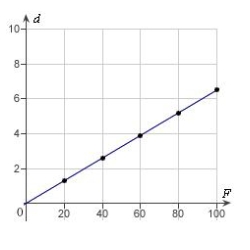
E)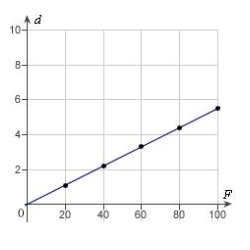
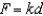 where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use a graphing utility to plot the data and graph the linear model.
where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use a graphing utility to plot the data and graph the linear model. 
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
7
Hooke's Law states that the force F required to compress or stretch a spring (within its elastic limits) is proportional to the distance d that the spring is compressed or stretched from its original length. That is, 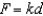 where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the regression capabilities of a graphing utility to find a linear model for the data. Round the numerical values in your answer to three decimal places.
where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the regression capabilities of a graphing utility to find a linear model for the data. Round the numerical values in your answer to three decimal places. 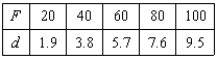
A)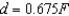
B)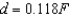
C)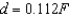
D)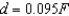
E)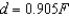
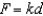 where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the regression capabilities of a graphing utility to find a linear model for the data. Round the numerical values in your answer to three decimal places.
where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the regression capabilities of a graphing utility to find a linear model for the data. Round the numerical values in your answer to three decimal places. 
A)
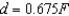
B)
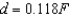
C)
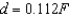
D)
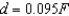
E)
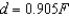

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
8
Students in a lab measured the breaking strength S (in pounds) of wood 2 inches thick, x inches high, and 12 inches long. The results are shown in the table below. Use the model 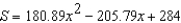 to approximate the breaking strength when
to approximate the breaking strength when 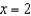 . Round your answer to two decimal places.
. Round your answer to two decimal places. 
A) 595.98 pounds
B) 390.19 pounds
C) 957.76 pounds
D) 801.77 pounds
E) 751.97 pounds
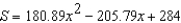 to approximate the breaking strength when
to approximate the breaking strength when 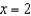 . Round your answer to two decimal places.
. Round your answer to two decimal places. 
A) 595.98 pounds
B) 390.19 pounds
C) 957.76 pounds
D) 801.77 pounds
E) 751.97 pounds

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
9
In an experiment, students measured the speed s (in meters per second) of a falling object t seconds after it was released. The results are shown in the table below. Use the regression capabilities of a graphing utility to find a linear model for the data. Round all numerical values in your answer to one decimal place. 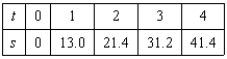
A)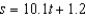
B)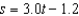
C)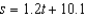
D)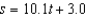
E)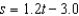

A)
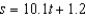
B)
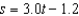
C)
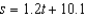
D)
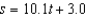
E)
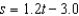

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
10
A V8 car engine is coupled to a dynamometer and the horsepower y is measured at different engine speeds x (in thousands of revolutions per minute). The results are shown in the table below. Use the regression capabilities of a graphing utility to find a cubic model for the data. Round the numerical values in your answer to three decimal places, where applicable. 
A)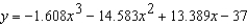
B)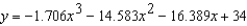
C)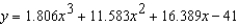
D)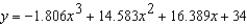
E)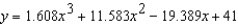

A)
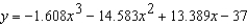
B)
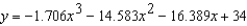
C)
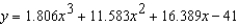
D)
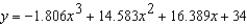
E)
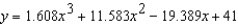

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
11
Hooke's Law states that the force F required to compress or stretch a spring (within its elastic limits) is proportional to the distance d that the spring is compressed or stretched from its original length. That is, 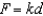 where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the model
where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the model 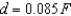 to estimate the elongation of the spring when a force of 55 newtons is applied. Round your answer to two decimal places.
to estimate the elongation of the spring when a force of 55 newtons is applied. Round your answer to two decimal places. 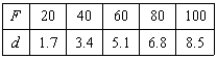
A) 8.08 cm
B) 6.38 cm
C) 4.68 cm
D) 2.98 cm
E) 9.78 cm
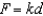 where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the model
where k is a measure of the stiffness of the spring and is called the spring constant. The table shows the elongation d in centimeters of a spring when a force of F newtons is applied. Use the model 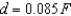 to estimate the elongation of the spring when a force of 55 newtons is applied. Round your answer to two decimal places.
to estimate the elongation of the spring when a force of 55 newtons is applied. Round your answer to two decimal places. 
A) 8.08 cm
B) 6.38 cm
C) 4.68 cm
D) 2.98 cm
E) 9.78 cm

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
12
Which function below would be most appropriate model for the given data? 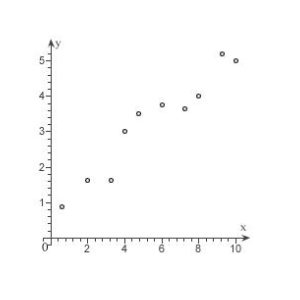
A) no apparent relationship between x and y
B) trigonometric
C) quadratic
D) linear

A) no apparent relationship between x and y
B) trigonometric
C) quadratic
D) linear

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
13
Determine which type of function would be most appropriate to fit the given data. 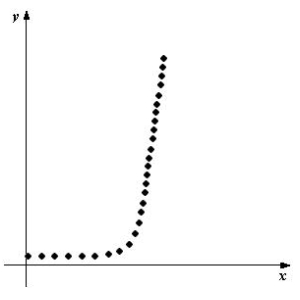
A) exponential
B) linear
C) quadratic
D) no relationship
E) trigonometric

A) exponential
B) linear
C) quadratic
D) no relationship
E) trigonometric

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
14
A V8 car engine is coupled to a dynamometer and the horsepower y is measured at different engine speeds x (in thousands of revolutions per minute). The results are shown in the table below. Use the model 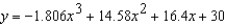 to approximate the horsepower when the engine is running at 5500 revolutions per minute. Round your answer to two decimal places.
to approximate the horsepower when the engine is running at 5500 revolutions per minute. Round your answer to two decimal places. 
A) 260.77 hp
B) 262.73 hp
C) 262.36 hp
D) 261.38 hp
E) 261.91 hp
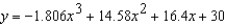 to approximate the horsepower when the engine is running at 5500 revolutions per minute. Round your answer to two decimal places.
to approximate the horsepower when the engine is running at 5500 revolutions per minute. Round your answer to two decimal places. 
A) 260.77 hp
B) 262.73 hp
C) 262.36 hp
D) 261.38 hp
E) 261.91 hp

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
15
The following ordered pairs represent temperatures in degrees Fahrenheit taken each hour from 1:00 pm until 5:00 pm. Let T be temperature, and let t be time, where 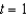 corresponds to 1:00 pm,
corresponds to 1:00 pm, 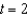 corresponds to 2:00 pm, and so on. Plot the data. Visually find a linear model for the data and find its equation. From the visual linear model that you created, determine which of the models that follow appears to best approximate the data. (1:00 pm ,
corresponds to 2:00 pm, and so on. Plot the data. Visually find a linear model for the data and find its equation. From the visual linear model that you created, determine which of the models that follow appears to best approximate the data. (1:00 pm , 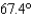 ), (2:00 pm ,
), (2:00 pm , 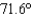 ), (3:00 pm ,
), (3:00 pm , 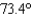 ), (4:00 pm ,
), (4:00 pm , 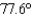 ), (5:00 pm ,
), (5:00 pm , 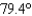 )
)
A)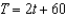
B)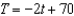
C)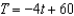
D)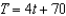
E)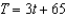
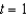 corresponds to 1:00 pm,
corresponds to 1:00 pm, 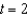 corresponds to 2:00 pm, and so on. Plot the data. Visually find a linear model for the data and find its equation. From the visual linear model that you created, determine which of the models that follow appears to best approximate the data. (1:00 pm ,
corresponds to 2:00 pm, and so on. Plot the data. Visually find a linear model for the data and find its equation. From the visual linear model that you created, determine which of the models that follow appears to best approximate the data. (1:00 pm , 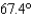 ), (2:00 pm ,
), (2:00 pm , 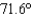 ), (3:00 pm ,
), (3:00 pm , 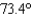 ), (4:00 pm ,
), (4:00 pm , 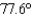 ), (5:00 pm ,
), (5:00 pm , 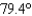 )
)A)
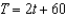
B)
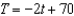
C)
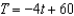
D)
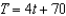
E)
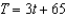

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
16
In an experiment, students measured the speed s (in meters per second) of a falling object t seconds after it was released. The results are shown in the table below. Use the regression capabilities of a graphing utility to find a linear model for the data. Round all numerical values in your answer to one decimal place. 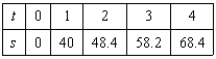
A)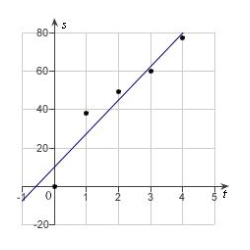
B)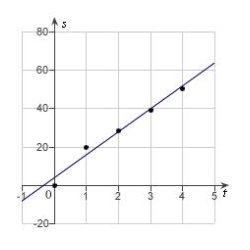
C)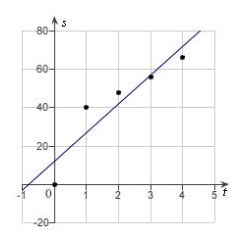
D)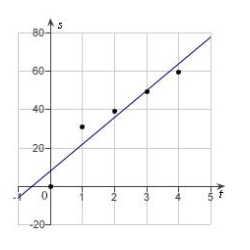
E)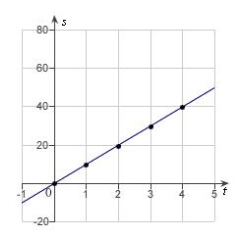

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck


