Deck 6: Analyzing Accumulated Change: Integrals in Action
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/51
Play
Full screen (f)
Deck 6: Analyzing Accumulated Change: Integrals in Action
1
The average quantity of sculptures that consumers will demand can be modeled as 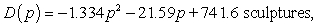 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 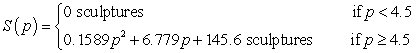 where the market price is p hundred dollars per sculpture. By how much will demand exceed supply at a price of $500 per sculpture?
where the market price is p hundred dollars per sculpture. By how much will demand exceed supply at a price of $500 per sculpture?
A) 581 sculptures
B) 183 sculptures
C) 600 sculptures
D) 417 sculptures
E) 784 sculptures
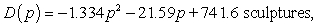 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 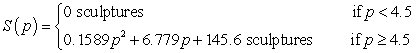 where the market price is p hundred dollars per sculpture. By how much will demand exceed supply at a price of $500 per sculpture?
where the market price is p hundred dollars per sculpture. By how much will demand exceed supply at a price of $500 per sculpture?A) 581 sculptures
B) 183 sculptures
C) 600 sculptures
D) 417 sculptures
E) 784 sculptures
417 sculptures
2
The daily demand for beef can be modeled by 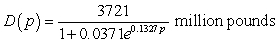 where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by
where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by 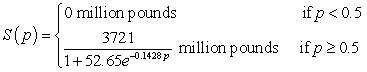 where the price for beef is p dollars per pound. How much beef is supplied when the price is $3.50 per pound? Round your answer to the nearest million pounds.
where the price for beef is p dollars per pound. How much beef is supplied when the price is $3.50 per pound? Round your answer to the nearest million pounds.
A) 113 million pounds
B) 74 million pounds
C) 121 million pounds
D) 105 million pounds
E) 0 million pounds
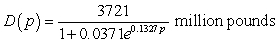 where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by
where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by 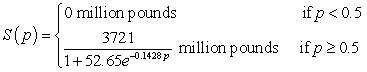 where the price for beef is p dollars per pound. How much beef is supplied when the price is $3.50 per pound? Round your answer to the nearest million pounds.
where the price for beef is p dollars per pound. How much beef is supplied when the price is $3.50 per pound? Round your answer to the nearest million pounds.A) 113 million pounds
B) 74 million pounds
C) 121 million pounds
D) 105 million pounds
E) 0 million pounds
113 million pounds
3
Evaluate the improper integral if it converges, or state that it diverges. 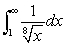
A)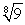
B)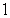
C)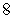
D)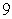
E) diverges
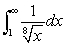
A)
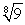
B)
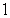
C)
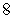
D)
E) diverges
diverges
4
In 1956, AT&T laid its first underwater phone line. By 1996, AT&T Submarine Systems, the division of AT&T that installs and maintains undersea communication lines, had seven cable ships and 1000 workers. On October 5, 1996, AT&T announced that it was seeking a buyer for its Submarine Systems division. The Submarine Systems division of AT&T was posting a profit of $850 million per year. If a prospective bidder considered that over a 25-year period, profits of the division would grow by 10% per year (after which it would be obsolete) and that profits could be reinvested at an annual return of 20%, what would the prospective bidder have considered to be the 25-year present value of its Submarine Systems division? Assume a continuous stream and round your answer to the nearest billion dollars. You may use technology to calculate the answer.
A) $4 billion
B) $3 billion
C) $8 billion
D) $9 billion
E) $126 billion
A) $4 billion
B) $3 billion
C) $8 billion
D) $9 billion
E) $126 billion

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
5
The willingness of saddle producers to supply saddles can be modeled by the following function: 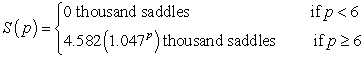 where saddles are sold for p thousand dollars. Find the producers' surplus when the market price is $7500. Round your answer to the nearest million dollars.
where saddles are sold for p thousand dollars. Find the producers' surplus when the market price is $7500. Round your answer to the nearest million dollars.
A) $9 million
B) $48 million
C) $39 million
D) $141 million
E) $6 million
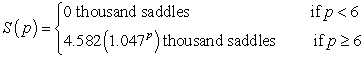 where saddles are sold for p thousand dollars. Find the producers' surplus when the market price is $7500. Round your answer to the nearest million dollars.
where saddles are sold for p thousand dollars. Find the producers' surplus when the market price is $7500. Round your answer to the nearest million dollars.A) $9 million
B) $48 million
C) $39 million
D) $141 million
E) $6 million

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
6
Between 1995 and 2001, the revenue of Sears Roebuck and Co. can be modeled as 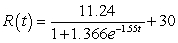 billion dollars per year, where t is the number of years after 1995. Assume that the revenue can be reinvested at 5.0% compounded annually. How much is Sears' revenue invested since 1995 worth in 2003? Round your answer to the nearest $10 billion.
billion dollars per year, where t is the number of years after 1995. Assume that the revenue can be reinvested at 5.0% compounded annually. How much is Sears' revenue invested since 1995 worth in 2003? Round your answer to the nearest $10 billion.
A) $270 billion
B) $330 billion
C) $880 billion
D) $130 billion
E) $400 billion
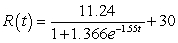 billion dollars per year, where t is the number of years after 1995. Assume that the revenue can be reinvested at 5.0% compounded annually. How much is Sears' revenue invested since 1995 worth in 2003? Round your answer to the nearest $10 billion.
billion dollars per year, where t is the number of years after 1995. Assume that the revenue can be reinvested at 5.0% compounded annually. How much is Sears' revenue invested since 1995 worth in 2003? Round your answer to the nearest $10 billion.A) $270 billion
B) $330 billion
C) $880 billion
D) $130 billion
E) $400 billion

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
7
The demand for train sets can be modeled as 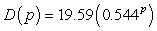 train sets where p is the price (in dollars) of a train set. For what prices is demand elastic?
train sets where p is the price (in dollars) of a train set. For what prices is demand elastic?
A)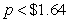 per train set
per train set
B)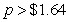 per train set
per train set
C)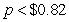 per train set
per train set
D)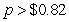 per train set
per train set
E)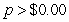 per train set
per train set
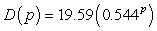 train sets where p is the price (in dollars) of a train set. For what prices is demand elastic?
train sets where p is the price (in dollars) of a train set. For what prices is demand elastic?A)
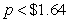 per train set
per train setB)
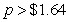 per train set
per train setC)
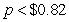 per train set
per train setD)
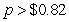 per train set
per train setE)
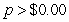 per train set
per train set
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
8
The demand for circus tickets can be modeled as 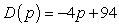 hundred tickets where p is the price (in dollars) of a ticket. According to the model, at what price will consumers no longer purchase circus tickets?
hundred tickets where p is the price (in dollars) of a ticket. According to the model, at what price will consumers no longer purchase circus tickets?
A) $23.50 per ticket
B) $94.00 per ticket
C) $4.04 per ticket
D) $117.50 per ticket
E) $8.00 per ticket
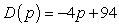 hundred tickets where p is the price (in dollars) of a ticket. According to the model, at what price will consumers no longer purchase circus tickets?
hundred tickets where p is the price (in dollars) of a ticket. According to the model, at what price will consumers no longer purchase circus tickets?A) $23.50 per ticket
B) $94.00 per ticket
C) $4.04 per ticket
D) $117.50 per ticket
E) $8.00 per ticket

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
9
The demand for train sets can be modeled as 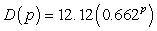 train sets where p is the price (in dollars) of a train set. Find the point of unit elasticity.
train sets where p is the price (in dollars) of a train set. Find the point of unit elasticity.
A) $5.58 per train set
B) $1.60 per train set
C) $29.38 per train set
D) $67.66 per train set
E) $2.42 per train set
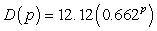 train sets where p is the price (in dollars) of a train set. Find the point of unit elasticity.
train sets where p is the price (in dollars) of a train set. Find the point of unit elasticity.A) $5.58 per train set
B) $1.60 per train set
C) $29.38 per train set
D) $67.66 per train set
E) $2.42 per train set

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
10
There are approximately 200 thousand northern fur seals. Suppose the population is being renewed at a rate of 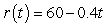 thousand seals per year and that the survival rate is 78% How many of the current population of 200 thousand seals will still be alive 25 years from now?
thousand seals per year and that the survival rate is 78% How many of the current population of 200 thousand seals will still be alive 25 years from now?
A) 244 seals
B) 401 seals
C) 514 seals
D) 201 seals
E) 156 seals
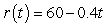 thousand seals per year and that the survival rate is 78% How many of the current population of 200 thousand seals will still be alive 25 years from now?
thousand seals per year and that the survival rate is 78% How many of the current population of 200 thousand seals will still be alive 25 years from now?A) 244 seals
B) 401 seals
C) 514 seals
D) 201 seals
E) 156 seals

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
11
The willingness of saddle producers to supply saddles can be modeled by the following function: 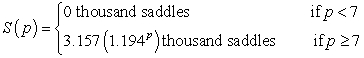 where saddles are sold for p thousand dollars. Find the producers' revenue when the market price is $7500. Round your answer to the nearest million dollars.
where saddles are sold for p thousand dollars. Find the producers' revenue when the market price is $7500. Round your answer to the nearest million dollars.
A) $84 million
B) $12 million
C) $3 million
D) $24 million
E) $90 million
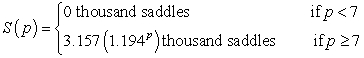 where saddles are sold for p thousand dollars. Find the producers' revenue when the market price is $7500. Round your answer to the nearest million dollars.
where saddles are sold for p thousand dollars. Find the producers' revenue when the market price is $7500. Round your answer to the nearest million dollars.A) $84 million
B) $12 million
C) $3 million
D) $24 million
E) $90 million

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
12
The willingness of saddle producers to supply saddles can be modeled by the following function: 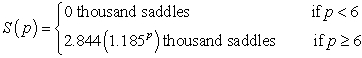 where saddles are sold for p thousand dollars. How many saddles will producers supply when the market price is $5000?
where saddles are sold for p thousand dollars. How many saddles will producers supply when the market price is $5000?
A) 6645 saddles
B) 30,000 saddles
C) 4347 saddles
D) 3323 saddles
E) 0 saddles
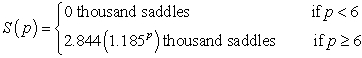 where saddles are sold for p thousand dollars. How many saddles will producers supply when the market price is $5000?
where saddles are sold for p thousand dollars. How many saddles will producers supply when the market price is $5000?A) 6645 saddles
B) 30,000 saddles
C) 4347 saddles
D) 3323 saddles
E) 0 saddles

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the improper integral if it converges, or state that it diverges. 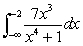
A)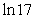
B)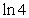
C)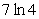
D)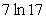
E) diverges
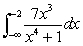
A)
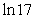
B)
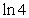
C)
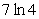
D)
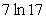
E) diverges

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
14
The average quantity of sculptures that consumers will demand can be modeled as 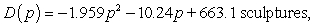 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 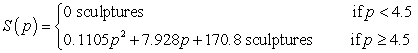 where the market price is p hundred dollars per sculpture. How much are consumers willing and able to spend for 74 sculptures? Round your answer to the nearest dollar.
where the market price is p hundred dollars per sculpture. How much are consumers willing and able to spend for 74 sculptures? Round your answer to the nearest dollar.
A) $110,433
B) $3907
C) $772,856
D) $114,340
E) $658,516
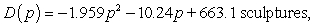 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 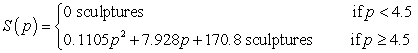 where the market price is p hundred dollars per sculpture. How much are consumers willing and able to spend for 74 sculptures? Round your answer to the nearest dollar.
where the market price is p hundred dollars per sculpture. How much are consumers willing and able to spend for 74 sculptures? Round your answer to the nearest dollar.A) $110,433
B) $3907
C) $772,856
D) $114,340
E) $658,516

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
15
For the 2002 fiscal year, Lowe's Companies, Inc., reported an annual net income of $1.023 billion. Assume the income can be reinvested continuously at an annual rate of return of 9.0% compounded continuously. Also assume that Lowe's will maintain this annual net income for the next 7 years. What is the future value of its 7-year net income? Round your answer to three decimal places.
A) $5.313 billion
B) $7.644 billion
C) $22.345 billion
D) $9.976 billion
E) $4.663 billion
A) $5.313 billion
B) $7.644 billion
C) $22.345 billion
D) $9.976 billion
E) $4.663 billion

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
16
The average quantity of sculptures that consumers will demand can be modeled as 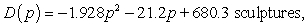 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 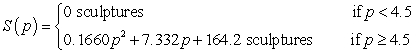 where the market price is p hundred dollars per sculpture. Determine the total social gain when sculptures are sold at the equilibrium price. Round your answer to the nearest dollar.
where the market price is p hundred dollars per sculpture. Determine the total social gain when sculptures are sold at the equilibrium price. Round your answer to the nearest dollar.
A) $295,907
B) $132,272
C) $182,553
D) $264,371
E) $700,605
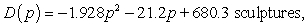 and the average quantity that producers will supply can be modeled as
and the average quantity that producers will supply can be modeled as 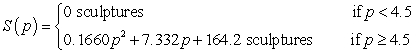 where the market price is p hundred dollars per sculpture. Determine the total social gain when sculptures are sold at the equilibrium price. Round your answer to the nearest dollar.
where the market price is p hundred dollars per sculpture. Determine the total social gain when sculptures are sold at the equilibrium price. Round your answer to the nearest dollar.A) $295,907
B) $132,272
C) $182,553
D) $264,371
E) $700,605

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the improper integral if it converges, or state that it diverges. 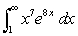
A)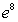
B)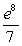
C)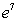
D)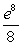
E) diverges
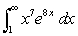
A)
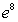
B)
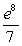
C)
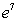
D)
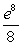
E) diverges

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
18
There were once more than 1 million elephants in West Africa. Now, however, the elephant population has dwindled to 19,000. Each year 17.8% of West Africa elephants die or are killed by hunters. At the same time, elephant births are decreasing by 13% per year. Considering that 47 elephants were born in the wild this year, estimate the elephant population of West Africa 27 years from now. You may use technology to calculate the answer.
A) 334 elephants
B) 111 elephants
C) 116 elephants
D) 457 elephants
E) 96 elephants
A) 334 elephants
B) 111 elephants
C) 116 elephants
D) 457 elephants
E) 96 elephants

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
19
The willingness of saddle producers to supply saddles can be modeled by the following function: 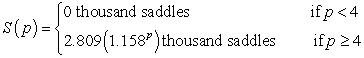 where saddles are sold for p thousand dollars. At what price will the producer supply 10 thousand saddles? Round your answer to the nearest dollar.
where saddles are sold for p thousand dollars. At what price will the producer supply 10 thousand saddles? Round your answer to the nearest dollar.
A) $1270 per saddle
B) $55,745 per saddle
C) $8178 per saddle
D) $5174 per saddle
E) $8656 per saddle
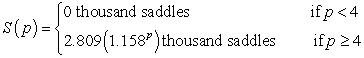 where saddles are sold for p thousand dollars. At what price will the producer supply 10 thousand saddles? Round your answer to the nearest dollar.
where saddles are sold for p thousand dollars. At what price will the producer supply 10 thousand saddles? Round your answer to the nearest dollar.A) $1270 per saddle
B) $55,745 per saddle
C) $8178 per saddle
D) $5174 per saddle
E) $8656 per saddle

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
20
The daily demand for beef can be modeled by 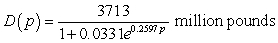 where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by
where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by 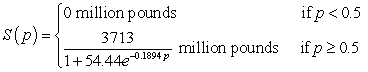 where the price for beef is p dollars per pound. Find the point of market equilibrium. Round your answer to two decimal places.
where the price for beef is p dollars per pound. Find the point of market equilibrium. Round your answer to two decimal places.
A) $16.49 per pound, 23.65 million pounds
B) $23.65 per pound, 16.49 million pounds
C) $16.49 per pound, 1093.27 million pounds
D) $1093.27 per pound, 16.49 million pounds
E) $3.33 per pound, 1093.27 million pounds
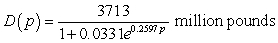 where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by
where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by 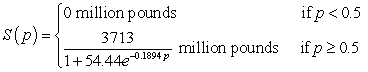 where the price for beef is p dollars per pound. Find the point of market equilibrium. Round your answer to two decimal places.
where the price for beef is p dollars per pound. Find the point of market equilibrium. Round your answer to two decimal places.A) $16.49 per pound, 23.65 million pounds
B) $23.65 per pound, 16.49 million pounds
C) $16.49 per pound, 1093.27 million pounds
D) $1093.27 per pound, 16.49 million pounds
E) $3.33 per pound, 1093.27 million pounds

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
21
Find a general solution for the following differential equation: 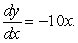
A)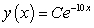
B)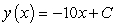
C)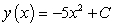
D)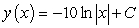
E)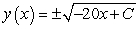
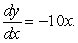
A)
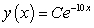
B)
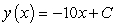
C)
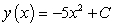
D)
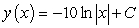
E)
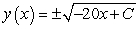

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
22
The height h, in feet, of a certain tree increases at a rate that is inversely proportional to time t, in years. The height of the tree is 8 feet at the end of 3 years, and reaches 23 feet at the end of 6 years. Write a differential equation describing the rate of change of the height of the tree, where k is the constant of proportionality (to be determined).
A)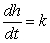 feet per year
feet per year
B)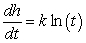 feet per year
feet per year
C)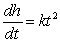 feet per year
feet per year
D)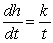 feet per year
feet per year
E)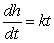 feet per year
feet per year
A)
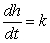 feet per year
feet per yearB)
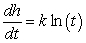 feet per year
feet per yearC)
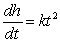 feet per year
feet per yearD)
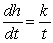 feet per year
feet per yearE)
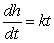 feet per year
feet per year
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
23
The rate of change with respect to time of the quantity q of pain reliever in a person's body t hours after the individual takes the medication is proportional to the quantity of medication remaining. Assume that 5 hours after a person takes 400 milligrams of a pain reliever, one-half of the original dose remains. How much pain reliever will remain after 10 hours? Round your answer to the nearest milligram.
A) 87 milligrams
B) 76 milligrams
C) 29 milligrams
D) 25 milligrams
E) 100 milligrams
A) 87 milligrams
B) 76 milligrams
C) 29 milligrams
D) 25 milligrams
E) 100 milligrams

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
24
Between 1975 and 1980, a country's energy production was increasing at a constant rate of 6.4 million Btu per year. In 1980 the country produced 37.1 million Btu. Using the initial condition, determine the particular solution for the county's energy production, where t is the number of years after 1975.
A)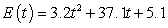 million Btu
million Btu
B)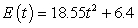 million Btu
million Btu
C)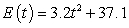 million Btu
million Btu
D)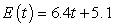 million Btu
million Btu
E)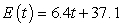 million Btu
million Btu
A)
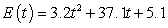 million Btu
million BtuB)
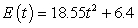 million Btu
million BtuC)
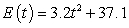 million Btu
million BtuD)
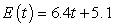 million Btu
million BtuE)
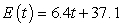 million Btu
million Btu
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
25
Find a general solution for the following differential equation: 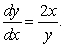
A)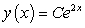
B)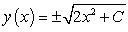
C)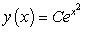
D)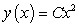
E)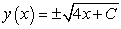
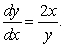
A)
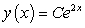
B)
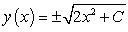
C)
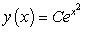
D)
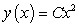
E)
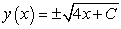

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
26
Find a general solution for the following differential equation: 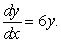
A)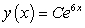
B)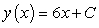
C)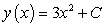
D)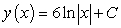
E)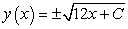
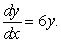
A)
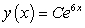
B)
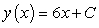
C)
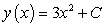
D)
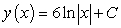
E)
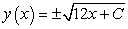

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
27
The height h, in feet, of a certain tree increases at a rate that is inversely proportional to time t, in years. The height of the tree is 9 feet at the end of 3 years, and reaches 22 feet at the end of 9 years. Give the particular solution for this height of the tree after t years. Round as necessary to two decimal places.
A)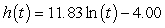 feet
feet
B)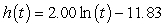 feet
feet
C)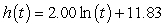 feet
feet
D)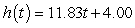 feet
feet
E)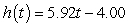 feet
feet
A)
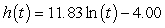 feet
feetB)
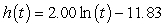 feet
feetC)
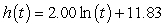 feet
feetD)
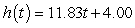 feet
feetE)
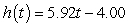 feet
feet
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
28
Between 1975 and 1980, a country's energy production was increasing at a constant rate of 6.6 million Btu per year. In 1980 the country produced 25.9 million Btu. Write a general solution for the county's energy production where t is the number of years after 1975.
A)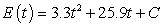 million Btu
million Btu
B)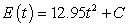 million Btu
million Btu
C)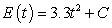 million Btu
million Btu
D)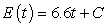 million Btu
million Btu
E)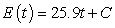 million Btu
million Btu
A)
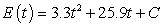 million Btu
million BtuB)
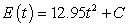 million Btu
million BtuC)
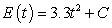 million Btu
million BtuD)
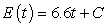 million Btu
million BtuE)
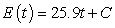 million Btu
million Btu
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
29
The number of patents issued for a certain product between 1950 and 1970 was increasing with respect to time at a rate jointly proportional to the number of patents already obtained and to the difference between the number of patents already obtained and the carrying capacity of the system. The carrying capacity was approximately 9000 patents, and the constant of proportionality was about 0.00068. By 1951, 3000 patents had been obtained. Find a particular solution for the number of patents t years after 1950.
A)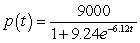 patents
patents
B)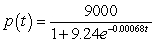 patents
patents
C)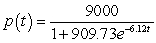 patents
patents
D)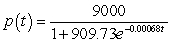 patents
patents
E)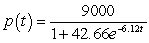 patents
patents
A)
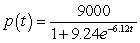 patents
patentsB)
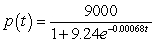 patents
patentsC)
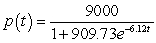 patents
patentsD)
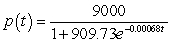 patents
patentsE)
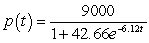 patents
patents
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
30
Find a general solution for the following differential equation: 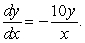
A)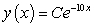
B)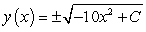
C)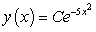
D)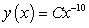
E)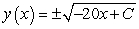
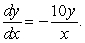
A)
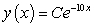
B)
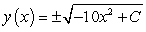
C)
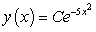
D)
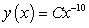
E)
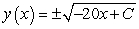

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
31
The number of patents issued for a certain product between 1950 and 1970 was increasing with respect to time at a rate jointly proportional to the number of patents already obtained and to the difference between the number of patents already obtained and the carrying capacity of the system. The carrying capacity was approximately 5000 patents, and the constant of proportionality was about 0.0003. By 1960, 2000 patents had been obtained. Write a differential equation describing the rate of change in the number of patents with respect to the number of years since 1950.
A)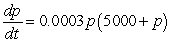 patents per year
patents per year
B)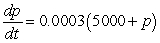 patents per year
patents per year
C)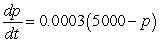 patents per year
patents per year
D)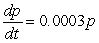 patents per year
patents per year
E)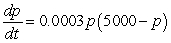 patents per year
patents per year
A)
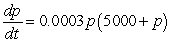 patents per year
patents per yearB)
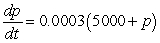 patents per year
patents per yearC)
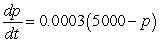 patents per year
patents per yearD)
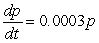 patents per year
patents per yearE)
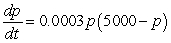 patents per year
patents per year
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
32
The rate of change with respect to time of the quantity q of pain reliever in a person's body t hours after the individual takes the medication is proportional to the quantity of medication remaining. Assume that 2 hours after a person takes 500 milligrams of a pain reliever, one-half of the original dose remains. Find a particular solution which gives the quantity of pain reliever in a person's body after t hours. Round coefficients to two decimal places.
A)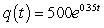 milligrams
milligrams
B)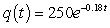 milligrams
milligrams
C)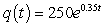 milligrams
milligrams
D)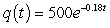 milligrams
milligrams
E)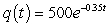 milligrams
milligrams
A)
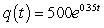 milligrams
milligramsB)
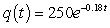 milligrams
milligramsC)
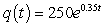 milligrams
milligramsD)
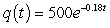 milligrams
milligramsE)
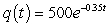 milligrams
milligrams
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
33
Assume the rate of change in the height h of a tree with respect to its age a is inversely proportional to the tree's height (with a proportionality constant of one). If the tree is 23 feet tall at age 21, how tall was the tree at age 5? Round your answer to the nearest foot.
A) 2 feet
B) 3 feet
C) 10 feet
D) 22 feet
E) 21 feet
A) 2 feet
B) 3 feet
C) 10 feet
D) 22 feet
E) 21 feet

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
34
For the first 9 months of life, the average weight w, in pounds, of a certain breed of dog increases at a rate that is inversely proportional to time t, in months. A 1-month-old puppy's weight is changing at a rate of 8 pounds per month, and a 9-month-old puppy weighs 90 pounds. Write a differential equation describing the rate of change of the weight of the puppy.
A)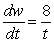 pounds per month
pounds per month
B)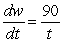 pounds per month
pounds per month
C)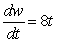 pounds per month
pounds per month
D)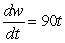 pounds per month
pounds per month
E)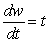 pounds per month
pounds per month
A)
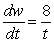 pounds per month
pounds per monthB)
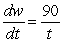 pounds per month
pounds per monthC)
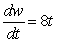 pounds per month
pounds per monthD)
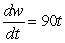 pounds per month
pounds per monthE)
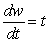 pounds per month
pounds per month
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
35
The number of patents issued for a certain product between 1950 and 1970 was increasing with respect to time at a rate jointly proportional to the number of patents already obtained and to the difference between the number of patents already obtained and the carrying capacity of the system. The carrying capacity was approximately 8000 patents, and the constant of proportionality was about 0.00024. By 1960, 4000 patents had been obtained. Find the general solution for the number of patents t years after 1950.
A)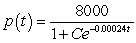 patents
patents
B)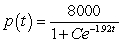 patents
patents
C)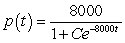 patents
patents
D)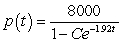 patents
patents
E)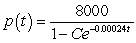 patents
patents
A)
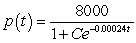 patents
patentsB)
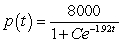 patents
patentsC)
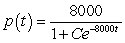 patents
patentsD)
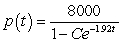 patents
patentsE)
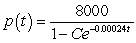 patents
patents
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
36
For the first 9 months of life, the average weight w, in pounds, of a certain breed of dog increases at a rate that is inversely proportional to time t, in months. A 1-month-old puppy's weight is changing at a rate of 7 pounds per month, and a 9-month-old puppy weighs 105 pounds. Find a particular solution for the weight of the puppy as a function of time. Round as necessary to one decimal place.
A)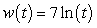 pounds
pounds
B)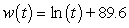 pounds
pounds
C)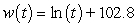 pounds
pounds
D)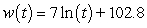 pounds
pounds
E)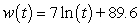 pounds
pounds
A)
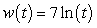 pounds
poundsB)
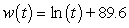 pounds
poundsC)
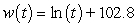 pounds
poundsD)
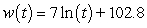 pounds
poundsE)
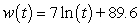 pounds
pounds
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
37
Barometric pressure p (measured in inches of mercury) decreases with respect to altitude a (measured in feet) at a rate that is directly proportional to the altitude. Assume the constant of proportionality is 0.003. Write a differential equation representing the rate of change of barometric pressure.
A)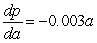 inches of mercury per foot
inches of mercury per foot
B)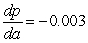 inches of mercury per foot
inches of mercury per foot
C)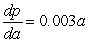 inches of mercury per foot
inches of mercury per foot
D)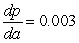 inches of mercury per foot
inches of mercury per foot
E)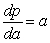 inches of mercury per foot
inches of mercury per foot
A)
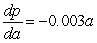 inches of mercury per foot
inches of mercury per footB)
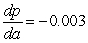 inches of mercury per foot
inches of mercury per footC)
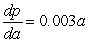 inches of mercury per foot
inches of mercury per footD)
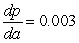 inches of mercury per foot
inches of mercury per footE)
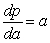 inches of mercury per foot
inches of mercury per foot
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
38
Find a general solution for the following differential equation: 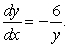
A)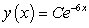
B)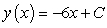
C)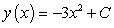
D)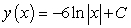
E)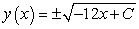
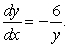
A)
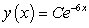
B)
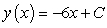
C)
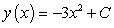
D)
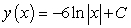
E)
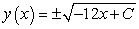

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
39
Find a general solution for the following differential equation: 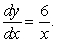
A)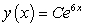
B)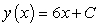
C)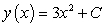
D)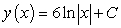
E)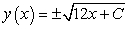
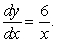
A)
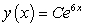
B)
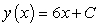
C)
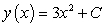
D)
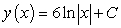
E)
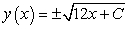

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
40
The rate of change with respect to time of the quantity q of pain reliever in a person's body t hours after the individual takes the medication is proportional to the quantity of medication remaining. Assume that 4 hours after a person takes 300 milligrams of a pain reliever, one-half of the original dose remains. Write a differential equation for the rate of change of the quantity of pain reliever in the body.
A)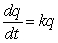 milligrams per hour
milligrams per hour
B)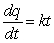 milligrams per hour
milligrams per hour
C)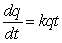 milligrams per hour
milligrams per hour
D)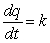 milligrams per hour
milligrams per hour
E)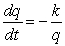 milligrams per hour
milligrams per hour
A)
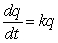 milligrams per hour
milligrams per hourB)
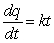 milligrams per hour
milligrams per hourC)
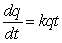 milligrams per hour
milligrams per hourD)
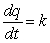 milligrams per hour
milligrams per hourE)
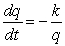 milligrams per hour
milligrams per hour
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
41
A person learns a new task at a rate that is equal to the percentage of the task not yet learned. Let p represent the percentage of the task already learned at time t (in hours). If a person begins learning at a rate of 19 percent per hour, write a differential equation describing the rate of change in the percentage of the task learned at time t.
A)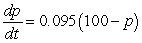 percent per hour
percent per hour
B)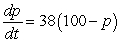 percent per hour
percent per hour
C)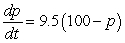 percent per hour
percent per hour
D)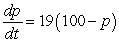 percent per hour
percent per hour
E)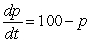 percent per hour
percent per hour
A)
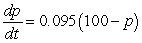 percent per hour
percent per hourB)
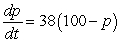 percent per hour
percent per hourC)
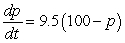 percent per hour
percent per hourD)
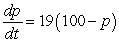 percent per hour
percent per hourE)
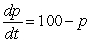 percent per hour
percent per hour
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
42
Find a general solution for the following differential equation: 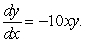
A)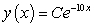
B)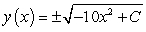
C)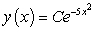
D)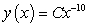
E)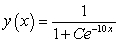
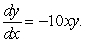
A)
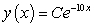
B)
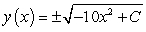
C)
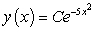
D)
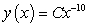
E)
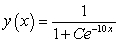

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
43
The rate of change in the number of jobs J for a Michigan roofing company is increasing by approximately 7.2 jobs per month squared. The number of jobs in January (m = 1) is decreasing at the rate of 1.7 jobs per month, and company records indicate that the company had 72 roofing jobs in February. Write a differential equation for the rate at which the rate of change in the number of roofing jobs for this company is changing.
A) jobs per month
jobs per month
B)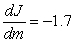 jobs per month
jobs per month
C)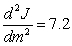 jobs per month squared
jobs per month squared
D)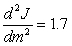 jobs per month squared
jobs per month squared
E)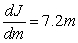 jobs per month
jobs per month
A)
 jobs per month
jobs per monthB)
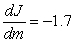 jobs per month
jobs per monthC)
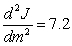 jobs per month squared
jobs per month squaredD)
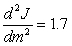 jobs per month squared
jobs per month squaredE)
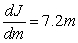 jobs per month
jobs per month
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
44
The rate of change in the number of jobs J for a Michigan roofing company is increasing by approximately 8 jobs per month squared. The number of jobs in January (m = 1) is decreasing at the rate of 1.7 jobs per month, and company records indicate that the company had 86 roofing jobs in February. Estimate the number of roofing jobs in August.
A) 326 jobs
B) 268 jobs
C) 392 jobs
D) 296 jobs
E) 115 jobs
A) 326 jobs
B) 268 jobs
C) 392 jobs
D) 296 jobs
E) 115 jobs

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
45
Newton's Law of Cooling says that the rate of change (with respect to time t in minutes) of the temperature T of an object is proportional to the difference between the temperature of the object and the temperature A of the object's surroundings. Initially, the object has a temperature of 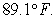 If the object is placed in a room where the temperature is fixed at
If the object is placed in a room where the temperature is fixed at 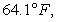 and the object begins to cool at a rate of 1.5 degrees
and the object begins to cool at a rate of 1.5 degrees 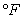 per minute, use Euler's method (with one step) to estimate the temperature of the object after 15 minutes. Round your answer to one decimal place.
per minute, use Euler's method (with one step) to estimate the temperature of the object after 15 minutes. Round your answer to one decimal place.
A)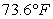
B)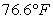
C)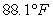
D)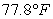
E)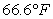
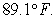 If the object is placed in a room where the temperature is fixed at
If the object is placed in a room where the temperature is fixed at 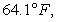 and the object begins to cool at a rate of 1.5 degrees
and the object begins to cool at a rate of 1.5 degrees 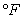 per minute, use Euler's method (with one step) to estimate the temperature of the object after 15 minutes. Round your answer to one decimal place.
per minute, use Euler's method (with one step) to estimate the temperature of the object after 15 minutes. Round your answer to one decimal place.A)
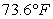
B)
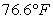
C)
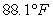
D)
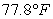
E)
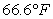

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
46
Newton's Law of Cooling says that the rate of change (with respect to time t in minutes) of the temperature T of an object is proportional to the difference between the temperature of the object and the temperature A of the object's surroundings. Initially, the object has a temperature of 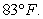 If the object is placed in a room where the temperature is fixed at
If the object is placed in a room where the temperature is fixed at 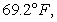 and the object begins to cool at a rate of 2.3 degrees
and the object begins to cool at a rate of 2.3 degrees 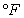 per minute, determine the constant of proportionality. Round your answer to four decimal places.
per minute, determine the constant of proportionality. Round your answer to four decimal places.
A) -0.3333
B) -2.3000
C) -0.1667
D) -4.6000
E) -6.0000
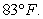 If the object is placed in a room where the temperature is fixed at
If the object is placed in a room where the temperature is fixed at 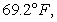 and the object begins to cool at a rate of 2.3 degrees
and the object begins to cool at a rate of 2.3 degrees 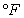 per minute, determine the constant of proportionality. Round your answer to four decimal places.
per minute, determine the constant of proportionality. Round your answer to four decimal places.A) -0.3333
B) -2.3000
C) -0.1667
D) -4.6000
E) -6.0000

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
47
Newton's Law of Cooling says that the rate of change (with respect to time t in minutes) of the temperature T of an object is proportional to the difference between the temperature of the object and the temperature A of the object's surroundings. If the object is placed in a room where the temperature is fixed at 71.4 degrees Fahrenheit, write a differential equation describing this law.
A)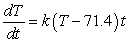 degrees Fahrenheit per minute
degrees Fahrenheit per minute
B)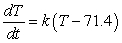 degrees Fahrenheit per minute
degrees Fahrenheit per minute
C)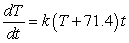 degrees Fahrenheit per minute
degrees Fahrenheit per minute
D)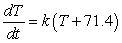 degrees Fahrenheit per minute
degrees Fahrenheit per minute
E)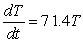 degrees Fahrenheit per minute
degrees Fahrenheit per minute
A)
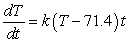 degrees Fahrenheit per minute
degrees Fahrenheit per minuteB)
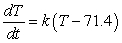 degrees Fahrenheit per minute
degrees Fahrenheit per minuteC)
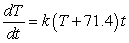 degrees Fahrenheit per minute
degrees Fahrenheit per minuteD)
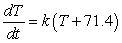 degrees Fahrenheit per minute
degrees Fahrenheit per minuteE)
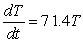 degrees Fahrenheit per minute
degrees Fahrenheit per minute
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
48
Between 1919 and 1995, the rate of change in the rate of change of the postage required to mail a first-class 1-ounce letter was approximately 0.022 cent per year squared. The postage was 2 cents in 1919, and it was increasing at the rate of approximately 0.393 cent per year in 1958. Using this information, estimate the postage that will be required to mail a first-class, 1-ounce letter in 2088.
A) $3.46
B) $3.26
C) $2.38
D) $1.46
E) $1.56
A) $3.46
B) $3.26
C) $2.38
D) $1.46
E) $1.56

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
49
A person learns a new task at a rate that is proportional to the percentage of the task not yet learned. Let p represent the percentage of the task already learned at time t (in hours). If a person begins learning at a rate of 39 percent per hour, estimate the percentage of the task that will be learned in 2 hours using Euler's method with a step size of 0.5. Round your answer to one decimal place.
A) 58.0 %
B) 66.8 %
C) 64.8 %
D) 49.4 %
E) 66.3 %
A) 58.0 %
B) 66.8 %
C) 64.8 %
D) 49.4 %
E) 66.3 %

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
50
When a spring is stretched and then released, it oscillates according to two laws of physics: Hooke's Law and Netwon's Second Law. These two laws combine to form the following differential equation in the case of free, undamped oscillation: 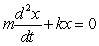 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with 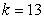 from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that
from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that 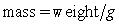 , where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
, where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
A)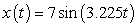
B)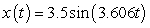
C)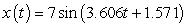
D)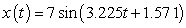
E)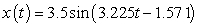
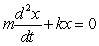 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with 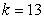 from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that
from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that 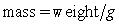 , where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
, where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.A)
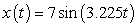
B)
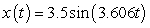
C)
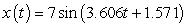
D)
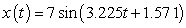
E)
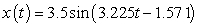

Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck
51
When a spring is stretched and then released, it oscillates according to two laws of physics: Hooke's Law and Netwon's Second Law. These two laws combine to form the following differential equation in the case of free, undamped oscillation: 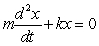 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with 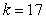 from which is hung a 68-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 3 feet farther than its equilibrium and released. Write a differential equation describing the acceleration of the spring with respect to time t measured in seconds. Use the fact that
from which is hung a 68-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 3 feet farther than its equilibrium and released. Write a differential equation describing the acceleration of the spring with respect to time t measured in seconds. Use the fact that 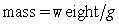 , where g is the gravitational constant 32 feet per second per second.
, where g is the gravitational constant 32 feet per second per second.
A)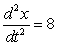 feet per second per second
feet per second per second
B)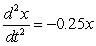 feet per second per second
feet per second per second
C)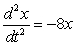 feet per second per second
feet per second per second
D)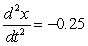 feet per second per second
feet per second per second
E)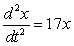 feet per second per second
feet per second per second
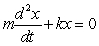 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with 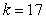 from which is hung a 68-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 3 feet farther than its equilibrium and released. Write a differential equation describing the acceleration of the spring with respect to time t measured in seconds. Use the fact that
from which is hung a 68-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 3 feet farther than its equilibrium and released. Write a differential equation describing the acceleration of the spring with respect to time t measured in seconds. Use the fact that 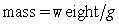 , where g is the gravitational constant 32 feet per second per second.
, where g is the gravitational constant 32 feet per second per second.A)
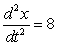 feet per second per second
feet per second per secondB)
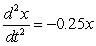 feet per second per second
feet per second per secondC)
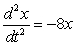 feet per second per second
feet per second per secondD)
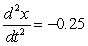 feet per second per second
feet per second per secondE)
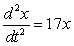 feet per second per second
feet per second per second
Unlock Deck
Unlock for access to all 51 flashcards in this deck.
Unlock Deck
k this deck


