Exam 6: Analyzing Accumulated Change: Integrals in Action
Exam 1: Ingredients of Change: Functions an Limits50 Questions
Exam 2: Describing Change: Rates47 Questions
Exam 3: Determining Change: Derivatives48 Questions
Exam 4: Analyzing Change: Applications of Derivatives50 Questions
Exam 5: Accumulating Change: Limits of Sums and the Definite Integral50 Questions
Exam 6: Analyzing Accumulated Change: Integrals in Action51 Questions
Exam 7: Ingredients of Multivariable Change: Models, Graphs, Rates46 Questions
Exam 8: Analyzing Multivariable Change: Optimization50 Questions
Select questions type
Find a general solution for the following differential equation: 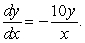
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
D
There are approximately 200 thousand northern fur seals. Suppose the population is being renewed at a rate of 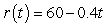 thousand seals per year and that the survival rate is 78% How many of the current population of 200 thousand seals will still be alive 25 years from now?
thousand seals per year and that the survival rate is 78% How many of the current population of 200 thousand seals will still be alive 25 years from now?
Free
(Multiple Choice)
5.0/5  (32)
(32)
Correct Answer:
B
Between 1975 and 1980, a country's energy production was increasing at a constant rate of 6.6 million Btu per year. In 1980 the country produced 25.9 million Btu. Write a general solution for the county's energy production where t is the number of years after 1975.
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
D
The height h, in feet, of a certain tree increases at a rate that is inversely proportional to time t, in years. The height of the tree is 8 feet at the end of 3 years, and reaches 23 feet at the end of 6 years. Write a differential equation describing the rate of change of the height of the tree, where k is the constant of proportionality (to be determined).
(Multiple Choice)
4.8/5  (29)
(29)
Find a general solution for the following differential equation: 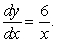
(Multiple Choice)
4.8/5  (37)
(37)
There were once more than 1 million elephants in West Africa. Now, however, the elephant population has dwindled to 19,000. Each year 17.8% of West Africa elephants die or are killed by hunters. At the same time, elephant births are decreasing by 13% per year. Considering that 47 elephants were born in the wild this year, estimate the elephant population of West Africa 27 years from now. You may use technology to calculate the answer.
(Multiple Choice)
4.9/5  (29)
(29)
The rate of change with respect to time of the quantity q of pain reliever in a person's body t hours after the individual takes the medication is proportional to the quantity of medication remaining. Assume that 5 hours after a person takes 400 milligrams of a pain reliever, one-half of the original dose remains. How much pain reliever will remain after 10 hours? Round your answer to the nearest milligram.
(Multiple Choice)
4.9/5  (36)
(36)
Between 1995 and 2001, the revenue of Sears Roebuck and Co. can be modeled as 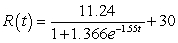 billion dollars per year, where t is the number of years after 1995. Assume that the revenue can be reinvested at 5.0% compounded annually. How much is Sears' revenue invested since 1995 worth in 2003? Round your answer to the nearest $10 billion.
billion dollars per year, where t is the number of years after 1995. Assume that the revenue can be reinvested at 5.0% compounded annually. How much is Sears' revenue invested since 1995 worth in 2003? Round your answer to the nearest $10 billion.
(Multiple Choice)
4.8/5  (37)
(37)
Newton's Law of Cooling says that the rate of change (with respect to time t in minutes) of the temperature T of an object is proportional to the difference between the temperature of the object and the temperature A of the object's surroundings. Initially, the object has a temperature of 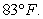 If the object is placed in a room where the temperature is fixed at
If the object is placed in a room where the temperature is fixed at 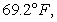 and the object begins to cool at a rate of 2.3 degrees
and the object begins to cool at a rate of 2.3 degrees 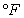 per minute, determine the constant of proportionality. Round your answer to four decimal places.
per minute, determine the constant of proportionality. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
The number of patents issued for a certain product between 1950 and 1970 was increasing with respect to time at a rate jointly proportional to the number of patents already obtained and to the difference between the number of patents already obtained and the carrying capacity of the system. The carrying capacity was approximately 5000 patents, and the constant of proportionality was about 0.0003. By 1960, 2000 patents had been obtained. Write a differential equation describing the rate of change in the number of patents with respect to the number of years since 1950.
(Multiple Choice)
4.9/5  (31)
(31)
The daily demand for beef can be modeled by 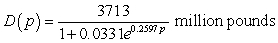 where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by
where the price for beef is p dollars per pound. Like-wise, the supply for beef can be modeled by 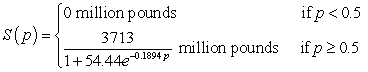 where the price for beef is p dollars per pound. Find the point of market equilibrium. Round your answer to two decimal places.
where the price for beef is p dollars per pound. Find the point of market equilibrium. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
The willingness of saddle producers to supply saddles can be modeled by the following function: 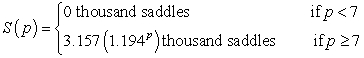 where saddles are sold for p thousand dollars. Find the producers' revenue when the market price is $7500. Round your answer to the nearest million dollars.
where saddles are sold for p thousand dollars. Find the producers' revenue when the market price is $7500. Round your answer to the nearest million dollars.
(Multiple Choice)
4.8/5  (40)
(40)
Newton's Law of Cooling says that the rate of change (with respect to time t in minutes) of the temperature T of an object is proportional to the difference between the temperature of the object and the temperature A of the object's surroundings. If the object is placed in a room where the temperature is fixed at 71.4 degrees Fahrenheit, write a differential equation describing this law.
(Multiple Choice)
4.7/5  (31)
(31)
When a spring is stretched and then released, it oscillates according to two laws of physics: Hooke's Law and Netwon's Second Law. These two laws combine to form the following differential equation in the case of free, undamped oscillation: 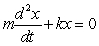 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with 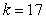 from which is hung a 68-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 3 feet farther than its equilibrium and released. Write a differential equation describing the acceleration of the spring with respect to time t measured in seconds. Use the fact that
from which is hung a 68-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 3 feet farther than its equilibrium and released. Write a differential equation describing the acceleration of the spring with respect to time t measured in seconds. Use the fact that 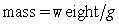 , where g is the gravitational constant 32 feet per second per second.
, where g is the gravitational constant 32 feet per second per second.
(Multiple Choice)
4.8/5  (41)
(41)
Between 1975 and 1980, a country's energy production was increasing at a constant rate of 6.4 million Btu per year. In 1980 the country produced 37.1 million Btu. Using the initial condition, determine the particular solution for the county's energy production, where t is the number of years after 1975.
(Multiple Choice)
4.8/5  (38)
(38)
The willingness of saddle producers to supply saddles can be modeled by the following function: 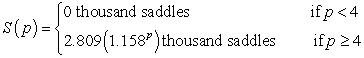 where saddles are sold for p thousand dollars. At what price will the producer supply 10 thousand saddles? Round your answer to the nearest dollar.
where saddles are sold for p thousand dollars. At what price will the producer supply 10 thousand saddles? Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (26)
(26)
When a spring is stretched and then released, it oscillates according to two laws of physics: Hooke's Law and Netwon's Second Law. These two laws combine to form the following differential equation in the case of free, undamped oscillation: 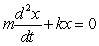 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point), t is time, and k is a constant associated with the strength of the spring. Consider a spring with 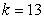 from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that
from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that 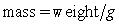 , where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
, where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
(Multiple Choice)
4.8/5  (26)
(26)
The demand for train sets can be modeled as 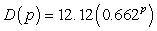 train sets where p is the price (in dollars) of a train set. Find the point of unit elasticity.
train sets where p is the price (in dollars) of a train set. Find the point of unit elasticity.
(Multiple Choice)
4.8/5  (25)
(25)
A person learns a new task at a rate that is equal to the percentage of the task not yet learned. Let p represent the percentage of the task already learned at time t (in hours). If a person begins learning at a rate of 19 percent per hour, write a differential equation describing the rate of change in the percentage of the task learned at time t.
(Multiple Choice)
4.8/5  (33)
(33)
Newton's Law of Cooling says that the rate of change (with respect to time t in minutes) of the temperature T of an object is proportional to the difference between the temperature of the object and the temperature A of the object's surroundings. Initially, the object has a temperature of 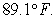 If the object is placed in a room where the temperature is fixed at
If the object is placed in a room where the temperature is fixed at 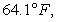 and the object begins to cool at a rate of 1.5 degrees
and the object begins to cool at a rate of 1.5 degrees 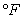 per minute, use Euler's method (with one step) to estimate the temperature of the object after 15 minutes. Round your answer to one decimal place.
per minute, use Euler's method (with one step) to estimate the temperature of the object after 15 minutes. Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (27)
(27)
Showing 1 - 20 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)