Deck 9: First-Order Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/72
Play
Full screen (f)
Deck 9: First-Order Differential Equations
1
The conversion of sucrose (table sugar) to glucose and fructose is first order in the concentration of sucrose, which means that the rate of reaction is proportional to the concentration of the sucrose. The rate of disappearance of sucrose can be expressed as 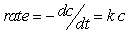 , where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/80 of its initial concentration?
, where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/80 of its initial concentration?
A) 21.91 hours
B) 0.020 hours
C) 400.00 hours
D) 128.76 hours
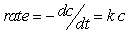 , where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/80 of its initial concentration?
, where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/80 of its initial concentration?A) 21.91 hours
B) 0.020 hours
C) 400.00 hours
D) 128.76 hours
21.91 hours
2
Find the solution of the differential equation, y' = -2y, satisfying the initial condition, y(-5) = 5.
A)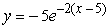
B)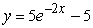
C)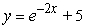
D)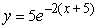
A)
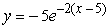
B)
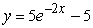
C)
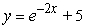
D)
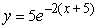
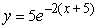
3
The number of bacteria in a culture increases exponentially with a growth constant of 0.3 hour-1. How long will it take for the population to increase from 6000 to 30,000 ?
A) 16.67 hours
B) 0.19 hour
C) 5.36 hours
D) 0.06 hour
A) 16.67 hours
B) 0.19 hour
C) 5.36 hours
D) 0.06 hour
5.36 hours
4
The rate at which water flows out of a drain in the bottom of a certain tank is proportional to the height of water in the tank. The tank is a vertical cylinder with cross-sectional area of 1.0 m2, so that every 1 cm in height represents 10 L. If the flow is 10 L/min (i.e. 1 cm/min) when the water level is 200 cm, how long will it take for the level to go from 200 cm to 20 cm?
A) 1060 minutes
B) 180 minutes
C) 7 minutes
D) 461 minutes
A) 1060 minutes
B) 180 minutes
C) 7 minutes
D) 461 minutes

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
5
The number of stores in a particular chain of coffee bars was 200 in 1990 and began growing exponentially with a growth constant of 0.20 year-1. In what year would one predict the number of stores to reach 10,000?
A) 2000
B) 2005
C) 2010
D) 2015
A) 2000
B) 2005
C) 2010
D) 2015

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
6
At the cafeteria, two identical glasses of juice were poured at the same time and put on the counter waiting for customers to take them. Their temperatures were 33oF when they were poured, and the cafeteria was a stable 72oF. One glass was 42oF when it was taken after 40 seconds. What was the temperature of the other when it was taken after 200 seconds?
A) 61.5oF
B) 64.7oF
C) 66.7oF
D) 58.3oF
A) 61.5oF
B) 64.7oF
C) 66.7oF
D) 58.3oF

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
7
The population of New Zealand grew exponentially through the 20th century at a rate of 1.6% year-1. If the population in 2000 was 3.9 million, when was the population 3.0 million?
A) 1984
B) 1989
C) 1994
D) 1999
A) 1984
B) 1989
C) 1994
D) 1999

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
8
The conversion of sucrose (table sugar) to glucose and fructose is first order in the concentration of sucrose, which means that the rate of reaction is proportional to the concentration of the sucrose. The rate of disappearance of sucrose can be expressed as 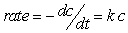 , where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If it takes 4 hours for the sucrose concentration to drop by a factor of 6, what is the rate constant?
, where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If it takes 4 hours for the sucrose concentration to drop by a factor of 6, what is the rate constant?
A) 0.41 hour-1
B) 0.67 hour-1
C) 0.45 hour-1
D) 1.50 hour-1
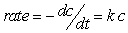 , where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If it takes 4 hours for the sucrose concentration to drop by a factor of 6, what is the rate constant?
, where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If it takes 4 hours for the sucrose concentration to drop by a factor of 6, what is the rate constant?A) 0.41 hour-1
B) 0.67 hour-1
C) 0.45 hour-1
D) 1.50 hour-1

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
9
$20,000 that was invested in 1990 was worth $147,740 in 2000. What annual interest rate did the investment earn in that 10 year period? Assume continuous compounding.
A) 119.03%
B) 12.02%
C) 99.03%
D) 20.00%
A) 119.03%
B) 12.02%
C) 99.03%
D) 20.00%

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
10
The Polymerase Chain Reaction (PCR) is used to replicate segments of DNA. It is used to make DNA samples big enough for testing, starting from very small samples collected, for instance, from a crime scene. PCR can double the number of a particular DNA segment every two minutes. Write an equation for the number of segments as a function of the number of minutes, t, if there is initially just one segment.
A)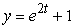
B)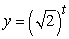
C)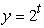
D)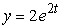
A)
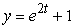
B)
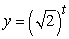
C)
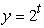
D)
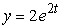

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
11
Find the solution of the differential equation, y' = 3y, satisfying the initial condition, y(0) = 1.
A)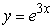
B)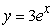

C)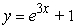
D)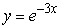
A)
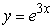
B)
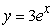

C)
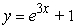
D)
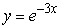

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
12
The Polymerase Chain Reaction (PCR) is used to replicate segments of DNA. It is used to make DNA samples big enough for testing, starting from very small samples collected, for instance, from a crime scene. PCR can double the number of a particular DNA segment every two minutes. If one wants a DNA sample with 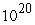 copies of a particular segment, how long must the PCR process be carried out to produce them? Assume that there is just one segment in the original sample.
copies of a particular segment, how long must the PCR process be carried out to produce them? Assume that there is just one segment in the original sample.
A) 133 minutes
B) 66 minutes
C) 23 minutes
D)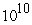 minutes
minutes
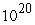 copies of a particular segment, how long must the PCR process be carried out to produce them? Assume that there is just one segment in the original sample.
copies of a particular segment, how long must the PCR process be carried out to produce them? Assume that there is just one segment in the original sample.A) 133 minutes
B) 66 minutes
C) 23 minutes
D)
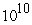 minutes
minutes
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
13
You select an insurance policy for your company that agrees to pay you the depreciated value of a piece of equipment if it is destroyed in an accident, but you have to choose one of two depreciation schedules when you begin the policy. One depreciation schedule is linear and depreciates the value to zero over 10 years. The other depreciation schedule is exponential and depreciates the value at a constant rate of 20% per year. An accident destroys the equipment after 5 years of ownership. Calculate the insurance company's obligation for each plan if the piece of equipment was valued initially at $100,000. Which depreciation schedule would have paid the most? (The cost of the policy is the same, no matter which depreciation schedule you choose.)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose the income tax structure is as follows: the first $16,000 is taxed at 10%, the remainder is taxed at 35%. Compute the tax 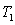 on an income of $40,000. Now suppose that inflation is 5% and you receive a cost of living (5%) raise to $42,000. Compute the tax
on an income of $40,000. Now suppose that inflation is 5% and you receive a cost of living (5%) raise to $42,000. Compute the tax 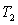 on this income. To compare the taxes you should adjust the tax
on this income. To compare the taxes you should adjust the tax 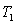 for inflation (add 5%).
for inflation (add 5%).
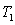 on an income of $40,000. Now suppose that inflation is 5% and you receive a cost of living (5%) raise to $42,000. Compute the tax
on an income of $40,000. Now suppose that inflation is 5% and you receive a cost of living (5%) raise to $42,000. Compute the tax 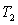 on this income. To compare the taxes you should adjust the tax
on this income. To compare the taxes you should adjust the tax 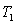 for inflation (add 5%).
for inflation (add 5%).
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
15
In 1965, Fairchild Semiconductor's R&D Director, Gordon Moore, noted that the maximum number of transistors that could be included cost effectively in one integrated circuit had been doubling yearly since 1959. While growth has not increased quite as quickly since 1965, it has still been exponential, and the continued exponential growth has become known as "Moore's Law". Considering that Intel's 4004 processor, introduced in 1971, had 2250 transistors, and their Pentium III processor, introduced in 1999, had 24,000,000 transistors, on average how long has it taken for processors to double the number of transistors they use.
A) 2.1 years
B) 0.6 years
C) 13.7 years
D) 0.3 years
A) 2.1 years
B) 0.6 years
C) 13.7 years
D) 0.3 years

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
16
An object's cooling constant, k, is often taken to be proportional to the its surface area. An iron ball cools from 350oC to 100oC in 30 seconds in a fast flowing stream of 30oC water. Use Newton's Law of Cooling to estimate how cool a similar volume of hot iron would become in 30 seconds if it were in the shape of a rod with surface area 3 times larger than the ball's.
A) 30.7oC
B) 75.9oC
C) 30.0oC
D) 33.3oC
A) 30.7oC
B) 75.9oC
C) 30.0oC
D) 33.3oC

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
17
Find the solution of the differential equation, y' = -4y, satisfying the initial condition, y(5) = 0.
A)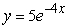
B)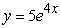
C)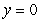
D)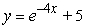
A)
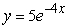
B)
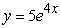
C)
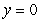
D)
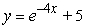

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
18
A treasury note that will be worth $100,000 in 10 years currently sells for $81,058. What constant interest rate does that correspond to?
A) 2.10%
B) 2.34%
C) 0.02%
D) 4.82%
A) 2.10%
B) 2.34%
C) 0.02%
D) 4.82%

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
19
Find the solution of the differential equation, y' = -3y, satisfying the condition, y(2) = 1.
A)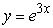
B)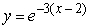
C)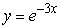
D)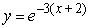
A)
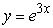
B)
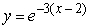
C)
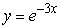
D)
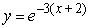

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
20
Find the solution of the differential equation, y' = -4y, satisfying the initial condition, y(0) = 7.
A)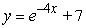
B)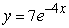
C)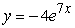
D)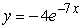
A)
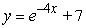
B)
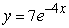
C)
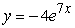
D)
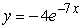

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
21
Is the following differential equation separable or not? 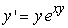
A) separable
B) not separable
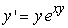
A) separable
B) not separable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
22
Is the following differential equation separable or not? 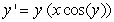
A) separable
B) not separable
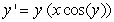
A) separable
B) not separable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the following initial value problem explicitly. 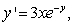 y(1) = -5
y(1) = -5
A)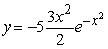
B)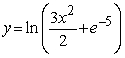
C)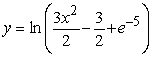
D)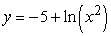
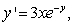 y(1) = -5
y(1) = -5A)
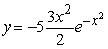
B)
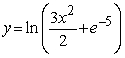
C)
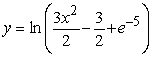
D)
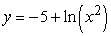

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
24
The differential equation is separable. Find the general solution in an explicit form. 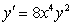
A)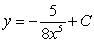
B)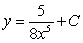
C)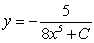
D)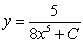
A)
B)
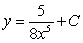
C)
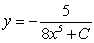
D)
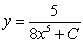

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
25
In 1995 an investor put $2500 in an account which paid 8%. In 2005 she withdrew $1500 from the account. What will the account be worth in 2020 ?
A) $16,972.64
B) $13,492.46
C) $7389.06
D) $4063.85
A) $16,972.64
B) $13,492.46
C) $7389.06
D) $4063.85

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
26
Is the following differential equation separable or not? 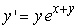
A) separable
B) not separable
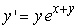
A) separable
B) not separable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the following initial value problem explicitly. 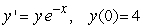
A)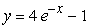
B)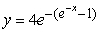
C)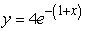
D)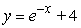
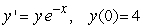
A)
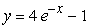
B)
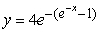
C)
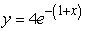
D)
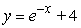

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the following initial value problem explicitly. 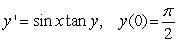 .
.
A)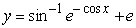
B)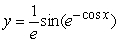
C)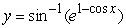
D)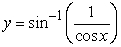
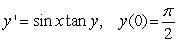 .
.A)
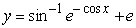
B)
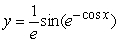
C)
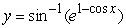
D)
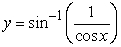

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
29
Find the solution to the following separable differential equation. 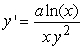 , a is a constant.
, a is a constant.
A)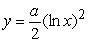
B)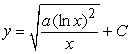
C)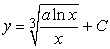
D)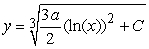
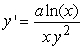 , a is a constant.
, a is a constant.A)
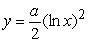
B)
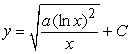
C)
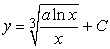
D)
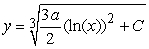

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
30
A stirred tank with volume, V, has a feed stream of concentrated floor cleaner flowing into it at a rate of f . The flow stream has a concentration of ci. The outlet stream also flows at f but with a concentration of c, the concentration of the floor cleaner solution in the tank. The rate of change of the concentration is proportional to the difference between ci and c with proportionality constant of f/V: 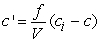 . If the tank volume is 1000 L, the flow rate is 10 L/min, the inlet concentration is 1.0, and the initial concentration of the floor cleaner in the tank is 0.0, how long until the concentration in the tank is 0.7?
. If the tank volume is 1000 L, the flow rate is 10 L/min, the inlet concentration is 1.0, and the initial concentration of the floor cleaner in the tank is 0.0, how long until the concentration in the tank is 0.7?
A) 12.0 minutes
B) 120.4 minutes
C) 100.0 minutes
D) 35.7 minutes
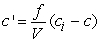 . If the tank volume is 1000 L, the flow rate is 10 L/min, the inlet concentration is 1.0, and the initial concentration of the floor cleaner in the tank is 0.0, how long until the concentration in the tank is 0.7?
. If the tank volume is 1000 L, the flow rate is 10 L/min, the inlet concentration is 1.0, and the initial concentration of the floor cleaner in the tank is 0.0, how long until the concentration in the tank is 0.7?A) 12.0 minutes
B) 120.4 minutes
C) 100.0 minutes
D) 35.7 minutes

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
31
Is the following differential equation separable or not? 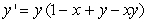
A) separable
B) not separable
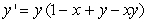
A) separable
B) not separable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
32
Calculate how much you would need to invest now in order to fund a year of college twenty years from now, assuming a year of college costs $19,000 now and is inflating at 7%, and your investment will earn 11%. Assume continuous compounding.
A) $8537
B) $2105
C) $4685
D) $42,285
A) $8537
B) $2105
C) $4685
D) $42,285

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
33
Find the solution to the following separable differential equation. 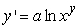 , a is a constant
, a is a constant
A)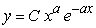
B)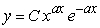
C)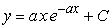
D)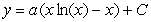
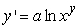 , a is a constant
, a is a constantA)
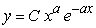
B)
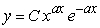
C)
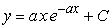
D)
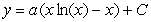

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
34
Find the solution to the following separable differential equation. 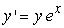
A)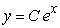
B)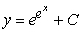
C)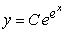
D)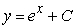
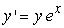
A)
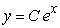
B)
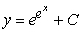
C)
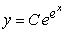
D)
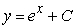

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
35
Find the solution to the following separable differential equation. 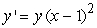
A)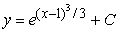
B)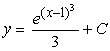
C)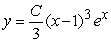
D)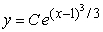
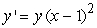
A)
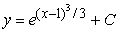
B)
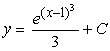
C)
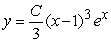
D)
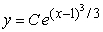

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
36
A bank offers to sell a bank note that will reach a maturity value of $15,000 in 9 years. How much should you pay for it now if you wish to receive an 8% return on your investment?
A) $1543.21
B) $7301.28
C) $13,800.00
D) $1533.33
A) $1543.21
B) $7301.28
C) $13,800.00
D) $1533.33

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
37
A particular investment program involves continuously making small investments adding up to $3600 each year. If the investment pays 8%, and the account started off with an initial balance of $1000, how much will the account be worth in 40 years?
A) $1,083,496
B) $1,058,964
C) $24,533
D) $1,128,496
A) $1,083,496
B) $1,058,964
C) $24,533
D) $1,128,496

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
38
The text describes logistic growth with an equation for the actual population in terms of a growth constant and a maximum population (carrying capacity), 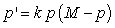 . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population,
. The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, 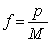 . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
. Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
if k = 0.00020 day-1 and M = 5000?
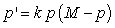 . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population,
. The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, 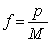 . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
. Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,if k = 0.00020 day-1 and M = 5000?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
39
The differential equation is separable. Find the general solution in an explicit form. 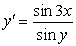
A)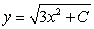
B)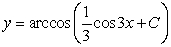
C)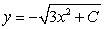
D)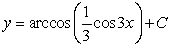
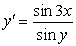
A)
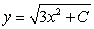
B)
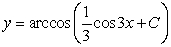
C)
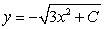
D)
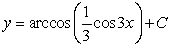

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the following initial value problem explicitly. 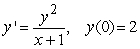
A)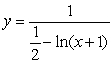
B)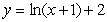
C)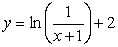
D)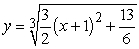
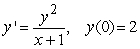
A)
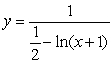
B)
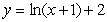
C)
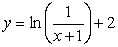
D)
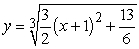

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
41
Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k1, and C can decompose to make A and B in a first order reaction with rate constant of k-1. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A0, B0, and C0, the change in C can be represented with the differential equation ![Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 2 , B<sub>0</sub> = 2, C<sub>0</sub> = 0, k<sub>1</sub> = 0.04, and k<sub>-1</sub> = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]](https://storage.examlex.com/TB5869/11eaa88b_9113_8f0e_a696_e18071ab97f7_TB5869_11.jpg) . If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
![Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 2 , B<sub>0</sub> = 2, C<sub>0</sub> = 0, k<sub>1</sub> = 0.04, and k<sub>-1</sub> = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]](https://storage.examlex.com/TB5869/11eaa88b_9113_8f0e_a696_e18071ab97f7_TB5869_11.jpg) . If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
42
The University of XYZ has a goal to increase its endowment from the initial value of $200,000,000, to $300,000,000 over 5 years. If the interest rate earned by the endowment (after expenses) is 5% each year (compounded continuously), and the contributions become available continuously and at a constant rate, how much will they actually have to collect from contributors over those 5 years to meet their goal?
A) $7,604,058
B) $78,994,498
C) $7,345,657,955
D) $38,020,292
A) $7,604,058
B) $78,994,498
C) $7,345,657,955
D) $38,020,292

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
43
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 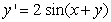 ,
, 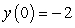 .
.
A) -3.5735, -4.6954
B) -3.9045, -4.7390
C) -3.5001, -4.5997
D) -3.4735, -4.5954
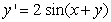 ,
, 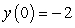 .
.A) -3.5735, -4.6954
B) -3.9045, -4.7390
C) -3.5001, -4.5997
D) -3.4735, -4.5954

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
44
A volume discount on a certain item is expressed as a differential equation in which the derivative of the price per item with respect to the number purchased is proportional to the difference between the price and some base price, below which the price can never go. If the price for just one item is $60, and the base price is $30, and the price per item when buying 10 items is $54, what is the price per item when buying 100 items?
A) $33
B) $48
C) $57
D) $46
A) $33
B) $48
C) $57
D) $46

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
45
Match the appropriate slope field with the differential equation 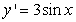 .
.
A)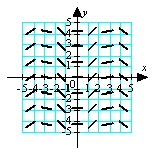
B)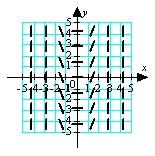
C)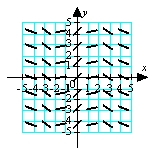
D)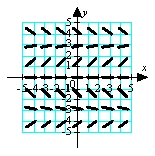
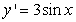 .
.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
46
Identify the equilibrium solutions for 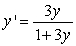 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.
A) y =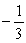 (unstable); y = 0 (stable)
(unstable); y = 0 (stable)
B) y =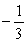 (stable); y = 0 (unstable)
(stable); y = 0 (unstable)
C) y = 0 (stable)
D) y = 0 (unstable)
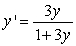 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.A) y =
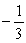 (unstable); y = 0 (stable)
(unstable); y = 0 (stable)B) y =
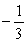 (stable); y = 0 (unstable)
(stable); y = 0 (unstable)C) y = 0 (stable)
D) y = 0 (unstable)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
47
An object falling freely through the atmosphere will accelerate due to the force of gravity at 9.86 m/s2 [Acceleration is the derivative of velocity with respect to time.] The atmosphere, however, will commonly exert a retarding force proportional to the object's velocity squared. The proportionality constant will depend largely on the object's shape. Write and solve the differential equation, then identify a free-falling object's terminal velocity (the limiting velocity) in terms of its drag proportionality constant, k. [To solve explicitly, you may use the initial condition v(0) = 0.]

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
48
Match the appropriate slope field with the differential equation 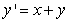 .
.
A)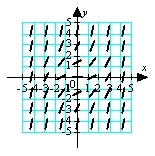
B)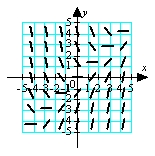
C)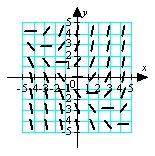
D)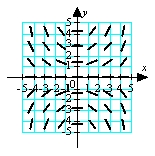
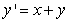 .
.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
49
Use the direction field below to sketch a solution curve and estimate the initial value y(0) for the differential equation 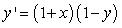 , such that the solution curve passes through the point (-1,-2).
, such that the solution curve passes through the point (-1,-2). 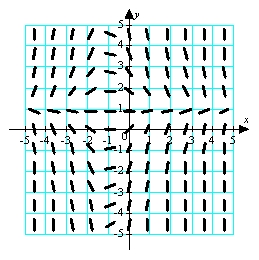
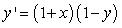 , such that the solution curve passes through the point (-1,-2).
, such that the solution curve passes through the point (-1,-2). 

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
50
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9115_8aea_a696_2ffcf4fa2c6f_TB5869_11.jpg)
![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9115_8aea_a696_2ffcf4fa2c6f_TB5869_11.jpg)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
51
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9116_001e_a696_ff524b547238_TB5869_11.jpg)
![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9116_001e_a696_ff524b547238_TB5869_11.jpg)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
52
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9115_b1fc_a696_29daeb5bed66_TB5869_11.jpg)
![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9115_b1fc_a696_29daeb5bed66_TB5869_11.jpg)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
53
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 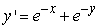 ,
, 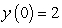 .
.
A) 1.4996, 0.5508
B) 2.7573, 3.0562
C) 2.7364, 3.0928
D) 2.8488, 3.1430
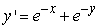 ,
, 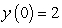 .
.A) 1.4996, 0.5508
B) 2.7573, 3.0562
C) 2.7364, 3.0928
D) 2.8488, 3.1430

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
54
Match the appropriate slope field with the differential equation 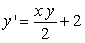 .
.
A)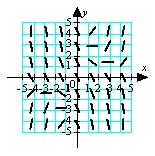
B)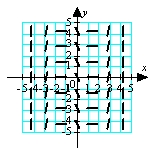
C)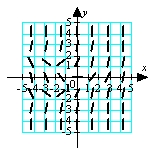
D)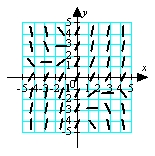
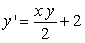 .
.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
55
Identify the equilibrium solutions for 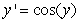 , for
, for 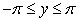 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.
A)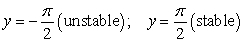
B)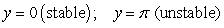
C)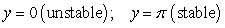
D)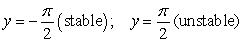
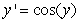 , for
, for 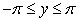 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.A)
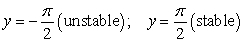
B)
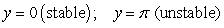
C)
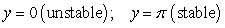
D)
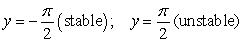

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
56
Construct a direction field for the differential equation. 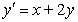

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
57
Construct a direction field for the differential equation. 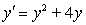

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
58
Identify the equilibrium solutions for 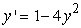 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.
A) y =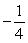 (unstable); y =
(unstable); y = 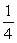 (stable)
(stable)
B) y =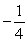 (stable); y =
(stable); y = 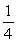 (stable)
(stable)
C) y =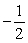 (stable); y =
(stable); y = 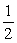 (stable)
(stable)
D) y =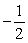 (unstable); y =
(unstable); y = 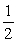 (stable)
(stable)
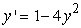 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.A) y =
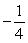 (unstable); y =
(unstable); y = 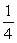 (stable)
(stable)B) y =
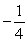 (stable); y =
(stable); y = 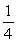 (stable)
(stable)C) y =
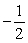 (stable); y =
(stable); y = 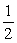 (stable)
(stable)D) y =
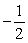 (unstable); y =
(unstable); y = 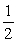 (stable)
(stable)
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
59
Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k1, and C can decompose to make A and B in a first order reaction with rate constant of k-1. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A0, B0, and C0, the change in C can be represented with the differential equation ![<strong>Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 0 , B<sub>0</sub> = 1, C<sub>0</sub> = 5, k<sub>1</sub> = 0.02 s <sup>-1</sup>, and k<sub>-1</sub> = 0.04 s<sup> -1</sup>, how much C is present after 15 seconds? [Note: c cannot be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]</strong> A) 8.36 B) 3.33 C) 4.81 D) 2.73](https://storage.examlex.com/TB5869/11eaa88b_9114_0441_a696_4361434e8a6c_TB5869_11.jpg) . If A0 = 0 , B0 = 1, C0 = 5, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 0 , B0 = 1, C0 = 5, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
A) 8.36
B) 3.33
C) 4.81
D) 2.73
![<strong>Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 0 , B<sub>0</sub> = 1, C<sub>0</sub> = 5, k<sub>1</sub> = 0.02 s <sup>-1</sup>, and k<sub>-1</sub> = 0.04 s<sup> -1</sup>, how much C is present after 15 seconds? [Note: c cannot be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]</strong> A) 8.36 B) 3.33 C) 4.81 D) 2.73](https://storage.examlex.com/TB5869/11eaa88b_9114_0441_a696_4361434e8a6c_TB5869_11.jpg) . If A0 = 0 , B0 = 1, C0 = 5, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 0 , B0 = 1, C0 = 5, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]A) 8.36
B) 3.33
C) 4.81
D) 2.73

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
60
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 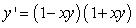 ,
, 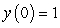 .
.
A) 1.38571, 0.58826
B) 1.26381, 0.54967
C) 1.61500, 0.13000
D) 1.42489, 0.58854
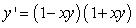 ,
, 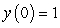 .
.A) 1.38571, 0.58826
B) 1.26381, 0.54967
C) 1.61500, 0.13000
D) 1.42489, 0.58854

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
61
Find all equilibrium points. 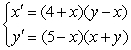
A)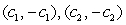 where
where 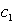 and
and 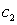 are any real numbers
are any real numbers
B)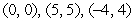
C)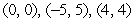
D)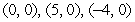
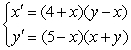
A)
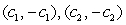 where
where 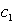 and
and 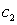 are any real numbers
are any real numbersB)
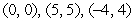
C)
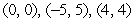
D)
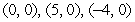

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
62
Find and interpret all equilibrium points for the competing species model. 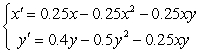
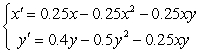

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
63
Use the following direction field to identify the stability of the equilibrium point (0.57, 0.14). 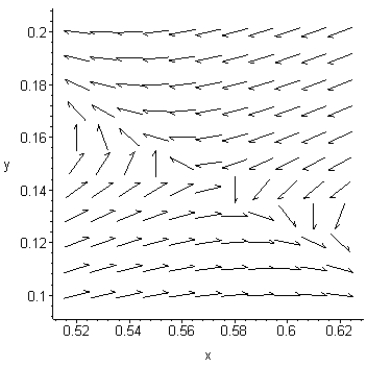
A) Stable
B) Unstable

A) Stable
B) Unstable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
64
Find all equilibrium points for the following coupled predator-prey-model equations. 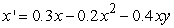
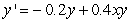
A) (0, 0), (1.500, 0), (0.500, 0.500)
B) (0, 0), (0.500, 0), (1.500, 0.500)
C) (0, 0), (0.500, 1.500), (0, 0.500)
D) (0, 0), (1.500, 0), (0.500, 0.250)
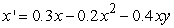
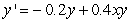
A) (0, 0), (1.500, 0), (0.500, 0.500)
B) (0, 0), (0.500, 0), (1.500, 0.500)
C) (0, 0), (0.500, 1.500), (0, 0.500)
D) (0, 0), (1.500, 0), (0.500, 0.250)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
65
Write the following second-order equation as a system of first-order equations. 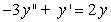
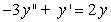

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
66
Find all equilibrium points for the following coupled equations. Identify each equilibrium point as stable or unstable. 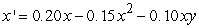
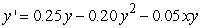
A) (0, 0)unstable; (1.33, 1.25)stable; (0.60, 0)unstable; (0, 1.10)unstable
B) (0, 0)unstable; (0, 0.20)unstable; (0.50, 0)unstable; (0.60, 0.20)stable
C) (0, 0)unstable; (0, 0.20)unstable; (0.60, 0)unstable; (1.33, 1.25)stable
D) (0, 0)unstable; (0, 1.25)unstable; (1.33, 0)unstable; (0.60, 1.10)stable
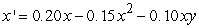
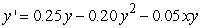
A) (0, 0)unstable; (1.33, 1.25)stable; (0.60, 0)unstable; (0, 1.10)unstable
B) (0, 0)unstable; (0, 0.20)unstable; (0.50, 0)unstable; (0.60, 0.20)stable
C) (0, 0)unstable; (0, 0.20)unstable; (0.60, 0)unstable; (1.33, 1.25)stable
D) (0, 0)unstable; (0, 1.25)unstable; (1.33, 0)unstable; (0.60, 1.10)stable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
67
Write the following third-order equation as a system of equations. 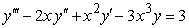
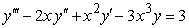

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
68
Find all equilibrium points for the following system of equations. 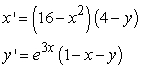
A)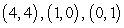
B)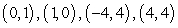
C)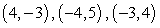
D)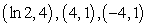
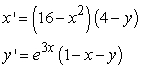
A)
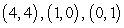
B)
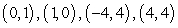
C)
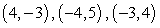
D)
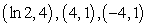

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
69
Use the direction field below to sketch a solution curve and estimate the initial value y(0) for the differential equation 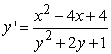 , such that the solution curve passes through the point (2, 2).
, such that the solution curve passes through the point (2, 2). 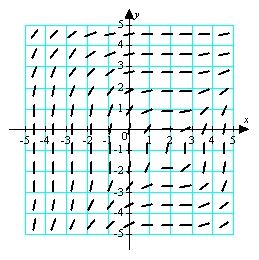
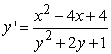 , such that the solution curve passes through the point (2, 2).
, such that the solution curve passes through the point (2, 2). 

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
70
Find all equilibrium points for the following system of equations. 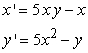
A)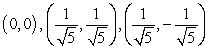
B)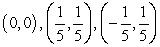
C)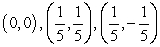
D)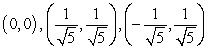
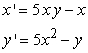
A)
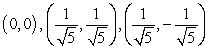
B)
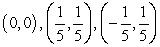
C)
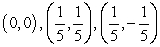
D)
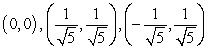

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
71
Write the following second-order equation as a system of first-order equations. 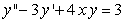
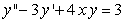

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
72
Use the following direction field to identify the stability of the equilibrium point (0.50, 0.84). 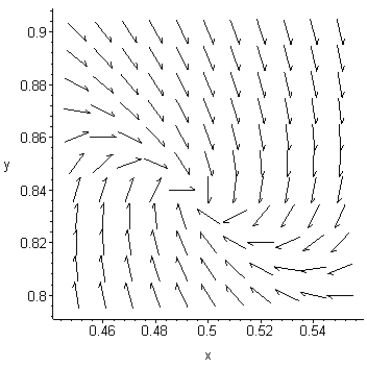
A) Stable
B) Unstable

A) Stable
B) Unstable

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck


