Exam 9: First-Order Differential Equations
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
Write the following second-order equation as a system of first-order equations. 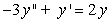
Free
(Essay)
4.8/5  (38)
(38)
Correct Answer:
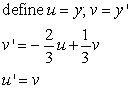
Find all equilibrium points for the following coupled equations. Identify each equilibrium point as stable or unstable. 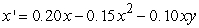
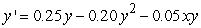
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
D
Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k1, and C can decompose to make A and B in a first order reaction with rate constant of k-1. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A0, B0, and C0, the change in C can be represented with the differential equation ![Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 0 , B<sub>0</sub> = 1, C<sub>0</sub> = 5, k<sub>1</sub> = 0.02 s <sup>-1</sup>, and k<sub>-1</sub> = 0.04 s<sup> -1</sup>, how much C is present after 15 seconds? [Note: c cannot be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]](https://storage.examlex.com/TB5869/11eaa88b_9114_0441_a696_4361434e8a6c_TB5869_11.jpg) . If A0 = 0 , B0 = 1, C0 = 5, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 0 , B0 = 1, C0 = 5, k1 = 0.02 s -1, and k-1 = 0.04 s -1, how much C is present after 15 seconds? [Note: c cannot be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
Free
(Multiple Choice)
4.7/5  (30)
(30)
Correct Answer:
B
Find the solution of the differential equation, y' = -3y, satisfying the condition, y(2) = 1.
(Multiple Choice)
4.8/5  (34)
(34)
Match the appropriate slope field with the differential equation 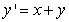 .
.
(Multiple Choice)
5.0/5  (35)
(35)
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 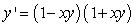 ,
, 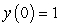 .
.
(Multiple Choice)
4.9/5  (30)
(30)
The Polymerase Chain Reaction (PCR) is used to replicate segments of DNA. It is used to make DNA samples big enough for testing, starting from very small samples collected, for instance, from a crime scene. PCR can double the number of a particular DNA segment every two minutes. If one wants a DNA sample with 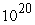 copies of a particular segment, how long must the PCR process be carried out to produce them? Assume that there is just one segment in the original sample.
copies of a particular segment, how long must the PCR process be carried out to produce them? Assume that there is just one segment in the original sample.
(Multiple Choice)
4.8/5  (41)
(41)
Write the following second-order equation as a system of first-order equations. 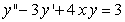
(Essay)
4.9/5  (36)
(36)
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 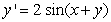 ,
, 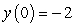 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Calculate how much you would need to invest now in order to fund a year of college twenty years from now, assuming a year of college costs $19,000 now and is inflating at 7%, and your investment will earn 11%. Assume continuous compounding.
(Multiple Choice)
4.8/5  (35)
(35)
Use the following direction field to identify the stability of the equilibrium point (0.57, 0.14). 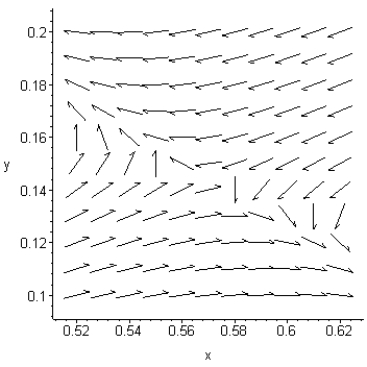
(Multiple Choice)
4.9/5  (34)
(34)
$20,000 that was invested in 1990 was worth $147,740 in 2000. What annual interest rate did the investment earn in that 10 year period? Assume continuous compounding.
(Multiple Choice)
4.8/5  (39)
(39)
Identify the equilibrium solutions for 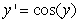 , for
, for 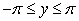 , and determine if they are stable or unstable.
, and determine if they are stable or unstable.
(Multiple Choice)
4.8/5  (38)
(38)
Use the following direction field to identify the stability of the equilibrium point (0.50, 0.84). 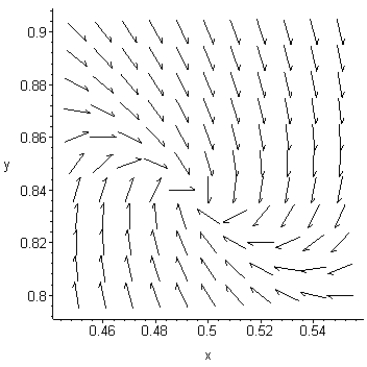
(Multiple Choice)
4.7/5  (38)
(38)
A bank offers to sell a bank note that will reach a maturity value of $15,000 in 9 years. How much should you pay for it now if you wish to receive an 8% return on your investment?
(Multiple Choice)
4.8/5  (35)
(35)
Find the solution of the differential equation, y' = -2y, satisfying the initial condition, y(-5) = 5.
(Multiple Choice)
5.0/5  (44)
(44)
The differential equation is separable. Find the general solution in an explicit form. 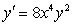
(Multiple Choice)
4.7/5  (36)
(36)
Use the direction field below to sketch a solution curve and estimate the initial value y(0) for the differential equation 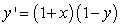 , such that the solution curve passes through the point (-1,-2).
, such that the solution curve passes through the point (-1,-2). 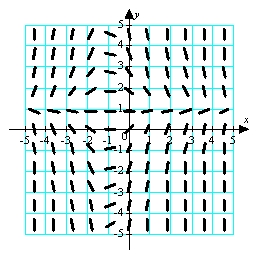
(Essay)
4.9/5  (31)
(31)
Find the solution of the differential equation, y' = 3y, satisfying the initial condition, y(0) = 1.
(Multiple Choice)
4.7/5  (43)
(43)
Showing 1 - 20 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)