Deck 5: Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/129
Play
Full screen (f)
Deck 5: Integration
1
The following table shows the velocity of a falling object at different times. For each time interval, estimate the distance fallen and the acceleration. Round to two decimal places. 

Some estimates are given in the table below. For example, during the time interval 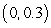 , an estimate of distance fallen is given by
, an estimate of distance fallen is given by 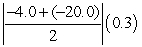 ft, and an estimate of acceleration is given by
ft, and an estimate of acceleration is given by 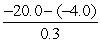 ft/s2.
ft/s2.
Other estimates are possible.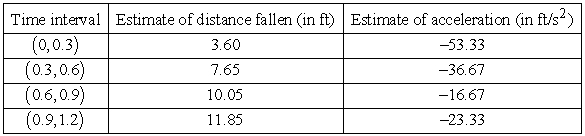

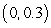 , an estimate of distance fallen is given by
, an estimate of distance fallen is given by 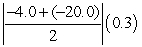 ft, and an estimate of acceleration is given by
ft, and an estimate of acceleration is given by 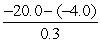 ft/s2.
ft/s2.Other estimates are possible.


2
Find the general antiderivative. 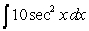
A)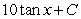
B)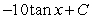
C)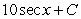
D)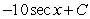
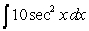
A)
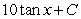
B)
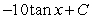
C)
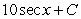
D)
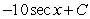
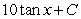
3
Find all functions satisfying the given conditions. 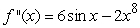
A)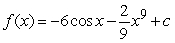
B)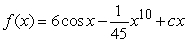
C)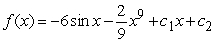
D)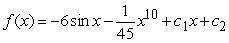
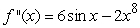
A)
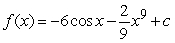
B)
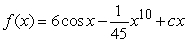
C)
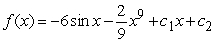
D)
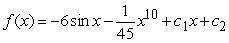
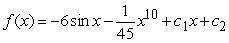
4
Find an antiderivative by reversing the chain rule, product rule or quotient rule. 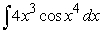
A)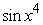
B)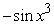
C)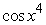
D)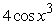
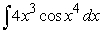
A)
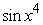
B)
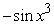
C)
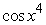
D)
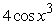

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that a car can come to rest from 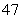 mph in
mph in 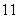 seconds. Assuming a constant (negative) acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the
seconds. Assuming a constant (negative) acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the 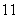 seconds (i.e., the stopping distance).
seconds (i.e., the stopping distance).
A) Acceleration =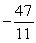 m/s2; distance =
m/s2; distance = 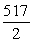 miles
miles
B) Acceleration =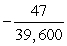 m/s2; distance =
m/s2; distance = 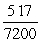 miles
miles
C) Acceleration =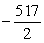 m/s2; distance =
m/s2; distance = 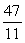 miles
miles
D) Acceleration =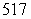 m/s2; distance =
m/s2; distance = 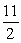 miles
miles
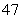 mph in
mph in 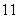 seconds. Assuming a constant (negative) acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the
seconds. Assuming a constant (negative) acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the 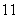 seconds (i.e., the stopping distance).
seconds (i.e., the stopping distance).A) Acceleration =
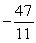 m/s2; distance =
m/s2; distance = 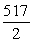 miles
milesB) Acceleration =
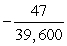 m/s2; distance =
m/s2; distance = 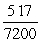 miles
milesC) Acceleration =
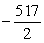 m/s2; distance =
m/s2; distance = 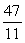 miles
milesD) Acceleration =
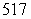 m/s2; distance =
m/s2; distance = 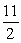 miles
miles
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
6
Determine the position function if the velocity function is 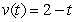 and the initial position is
and the initial position is 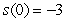 .
.
A)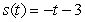
B)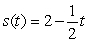
C)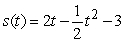
D)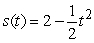
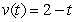 and the initial position is
and the initial position is 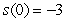 .
.A)
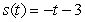
B)
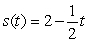
C)
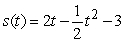
D)
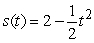

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
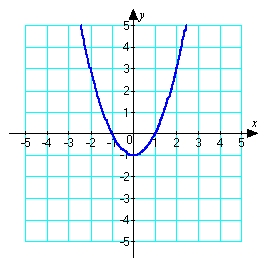
7
Sketch a graph of a function 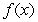 corresponding to the given graph of
corresponding to the given graph of 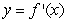 .
. 
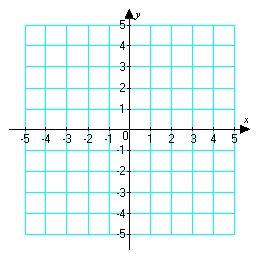
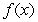 corresponding to the given graph of
corresponding to the given graph of 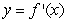 .
. 


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
8
Sketch a graph of a function 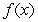 corresponding to the given graph of
corresponding to the given graph of 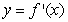 .
. 
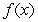 corresponding to the given graph of
corresponding to the given graph of 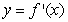 .
. 


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
9
Find the function 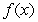 satisfying the given conditions.
satisfying the given conditions. 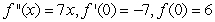
A)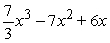
B)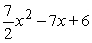
C)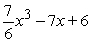
D)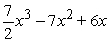
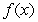 satisfying the given conditions.
satisfying the given conditions. 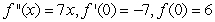
A)
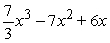
B)
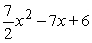
C)
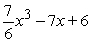
D)
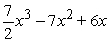

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
10
Find the general antiderivative. 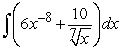
A)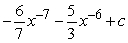
B)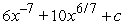
C)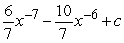
D)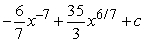
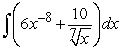
A)
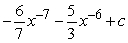
B)
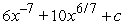
C)
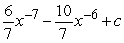
D)
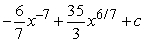

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
11
The following table shows the acceleration of a car moving in a straight line. If the car is traveling 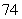 ft/s at time
ft/s at time 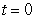 , estimate the speed and distance traveled at each time.
, estimate the speed and distance traveled at each time. 
 ft/s at time
ft/s at time 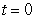 , estimate the speed and distance traveled at each time.
, estimate the speed and distance traveled at each time. 

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
12
Find the function 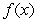 satisfying the given conditions.
satisfying the given conditions. 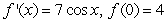
A)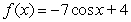
B)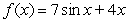
C)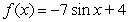
D)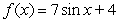
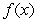 satisfying the given conditions.
satisfying the given conditions. 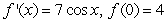
A)
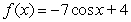
B)
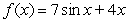
C)
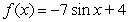
D)
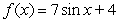

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
13
Find a function f (x) such that point (1, 2) is in the graph of y = f (x), the slope of the tangent line at (1, 2) is -5, and f ''(x) = x - 1
A)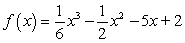
B)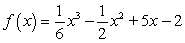
C)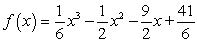
D)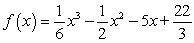
A)
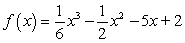
B)
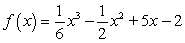
C)
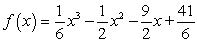
D)
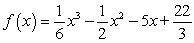

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose that a car can accelerate from 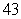 mph to
mph to 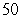 mph in
mph in 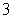 seconds. Assuming a constant acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the
seconds. Assuming a constant acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the 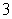 seconds.
seconds.
A) Acceleration =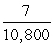 m/s22; distance =
m/s22; distance = 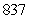 miles
miles
B) Acceleration =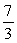 m/s22; distance =
m/s22; distance = 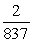 miles
miles
C) Acceleration =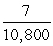 m/s22; distance =
m/s22; distance = 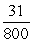 miles
miles
D) Acceleration =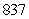 m/s22; distance =
m/s22; distance = 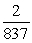 miles
miles
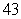 mph to
mph to 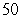 mph in
mph in 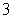 seconds. Assuming a constant acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the
seconds. Assuming a constant acceleration, find the acceleration (in miles per second squared) of the car and find the distance traveled by the car during the 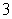 seconds.
seconds.A) Acceleration =
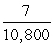 m/s22; distance =
m/s22; distance = 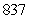 miles
milesB) Acceleration =
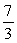 m/s22; distance =
m/s22; distance = 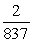 miles
milesC) Acceleration =
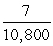 m/s22; distance =
m/s22; distance = 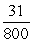 miles
milesD) Acceleration =
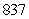 m/s22; distance =
m/s22; distance = 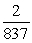 miles
miles
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
15
Find the general antiderivative. 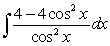
A) -4tan x - 4x + c
B) 4tan x - 4x + c
C) 4cot x - 4x + c
D) -4cot x - 4x + c
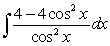
A) -4tan x - 4x + c
B) 4tan x - 4x + c
C) 4cot x - 4x + c
D) -4cot x - 4x + c

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
16
Find the general antiderivative. 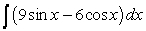
A)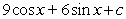
B)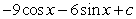
C)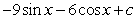
D)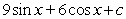
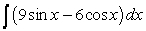
A)
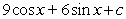
B)
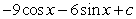
C)
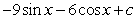
D)
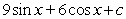

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
17
Determine the position function if the acceleration function is 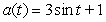 , the initial velocity is
, the initial velocity is 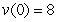 , and the initial position is
, and the initial position is 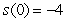 .
.
A)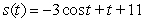
B)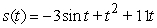
C)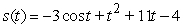
D)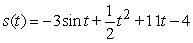
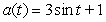 , the initial velocity is
, the initial velocity is 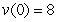 , and the initial position is
, and the initial position is 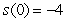 .
.A)
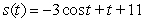
B)
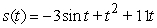
C)
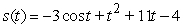
D)
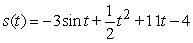

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
18
Find an antiderivative by reversing the chain rule, product rule or quotient rule. 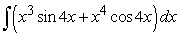
A)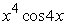
B)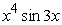
C)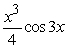
D)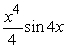
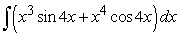
A)
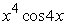
B)
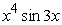
C)
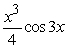
D)
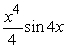

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
19
Translate into summation notation. 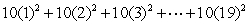
A)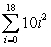
B)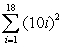
C)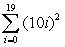
D)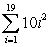
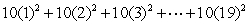
A)
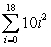
B)
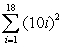
C)
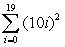
D)
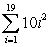

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
20
Find the general antiderivative. 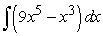
A)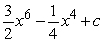
B)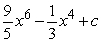
C)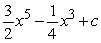
D)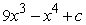
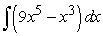
A)
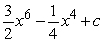
B)
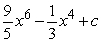
C)
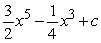
D)
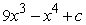

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
21
Use summation rules to compute the sum. 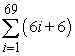
A)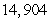
B)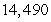
C)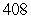
D)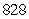
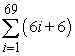
A)
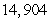
B)
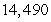
C)
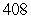
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
22
The table shows the velocity of a projectile at various times. Estimate the distance traveled. Round to two decimal places. 


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose that a runner has velocity 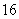 mph for
mph for 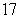 minutes, velocity
minutes, velocity 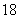 mph for
mph for 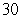 minutes, velocity
minutes, velocity 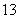 mph for
mph for 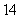 minutes, and velocity
minutes, and velocity 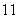 mph for
mph for 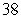 minutes. Find the distance run. Round to two decimal places.
minutes. Find the distance run. Round to two decimal places.
A)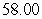 miles
miles
B)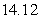 miles
miles
C)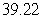 miles
miles
D)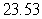 miles
miles
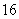 mph for
mph for 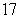 minutes, velocity
minutes, velocity 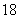 mph for
mph for 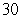 minutes, velocity
minutes, velocity 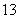 mph for
mph for 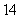 minutes, and velocity
minutes, and velocity 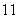 mph for
mph for 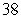 minutes. Find the distance run. Round to two decimal places.
minutes. Find the distance run. Round to two decimal places.A)
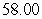 miles
milesB)
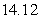 miles
milesC)
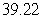 miles
milesD)
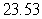 miles
miles
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
24
Use summation rules to compute the sum. 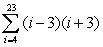
A) 4130
B) 69,300
C) 72,891
D) 4301
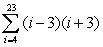
A) 4130
B) 69,300
C) 72,891
D) 4301

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
25
Translate the following calculation into summation notation and then compute the sum. The sum of the squares of the first 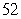 positive integers.
positive integers.
A)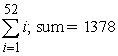
B)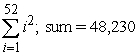
C)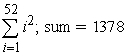
D)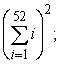 sum =
sum = 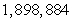
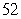 positive integers.
positive integers.A)
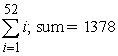
B)
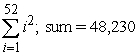
C)
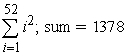
D)
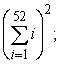 sum =
sum = 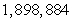

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
26
Compute the sum of the form 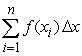 for the given function and
for the given function and 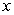 -values, with
-values, with 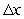 equal to the difference in adjacent
equal to the difference in adjacent 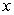 's.
's. 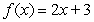 ;
; 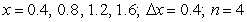
A)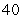
B)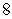
C)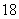
D)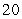
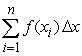 for the given function and
for the given function and 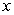 -values, with
-values, with 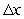 equal to the difference in adjacent
equal to the difference in adjacent 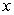 's.
's. 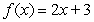 ;
; 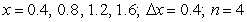
A)
B)
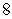
C)
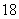
D)
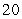

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
27
Use mathematical induction to prove that 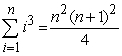 for all integers
for all integers 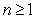 .
.
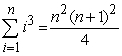 for all integers
for all integers 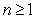 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
28
Use summation rules to compute the sum. 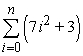
A)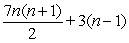
B)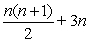
C)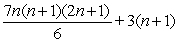
D)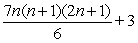
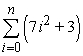
A)
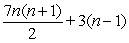
B)
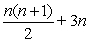
C)
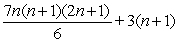
D)
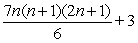

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose that a car has velocity 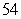 mph for
mph for 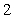 hours, velocity
hours, velocity 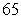 mph for
mph for 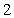 hours, velocity
hours, velocity 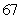 mph for
mph for 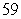 minutes, and velocity
minutes, and velocity 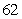 mph for
mph for 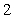 hours. Find the distance traveled. Round to two decimal places.
hours. Find the distance traveled. Round to two decimal places.
A)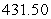 miles
miles
B)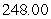 miles
miles
C)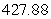 miles
miles
D)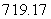 miles
miles
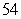 mph for
mph for  hours, velocity
hours, velocity 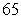 mph for
mph for 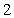 hours, velocity
hours, velocity 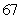 mph for
mph for 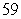 minutes, and velocity
minutes, and velocity 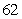 mph for
mph for 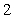 hours. Find the distance traveled. Round to two decimal places.
hours. Find the distance traveled. Round to two decimal places.A)
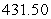 miles
milesB)
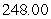 miles
milesC)
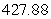 miles
milesD)
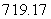 miles
miles
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
30
Compute the sum of the form 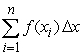 for the given function and
for the given function and 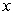 -values, with
-values, with 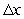 equal to the difference in adjacent
equal to the difference in adjacent 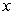 's.
's. 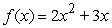 ;
; 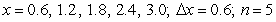
A)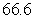
B)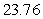
C)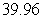
D)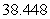
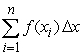 for the given function and
for the given function and 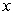 -values, with
-values, with 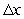 equal to the difference in adjacent
equal to the difference in adjacent 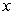 's.
's. 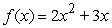 ;
; 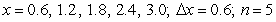
A)
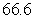
B)
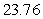
C)
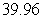
D)
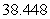

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
31
Use summation rules to compute the sum. 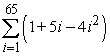
A)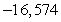
B)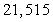
C)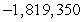
D)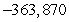
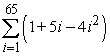
A)
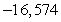
B)
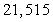
C)
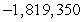
D)
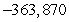

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
32
Write out all terms and compute the sum. 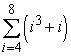
A)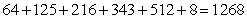
B)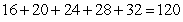
C)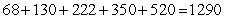
D)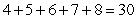
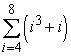
A)
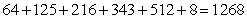
B)
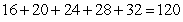
C)
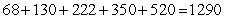
D)
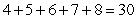

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
33
Write out all terms and compute the sum. 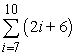
A)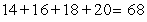
B)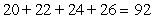
C)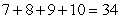
D)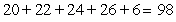
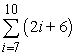
A)
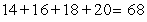
B)
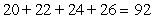
C)
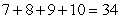
D)
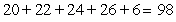

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
34
List the evaluation points corresponding to the midpoint of each subinterval, sketch the function and corresponding approximating rectangles and evaluate the corresponding Riemann sum. Round the sum to two decimal places. 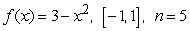
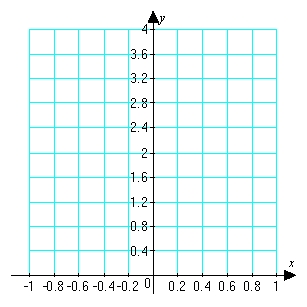
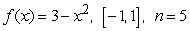


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
35
Compute the sum and the limit of the sum as 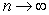 .
. 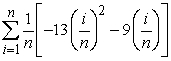
A) Sum =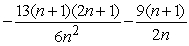 ; limit of sum as
; limit of sum as 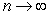 is
is 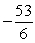

B) Sum =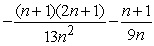 ; limit of sum as
; limit of sum as 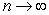 is
is 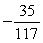

C) Sum =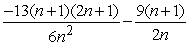 ; limit of sum as
; limit of sum as 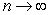 is
is 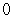

D) Sum =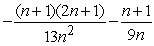 ; limit of sum as
; limit of sum as 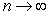 is
is 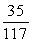

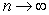 .
. 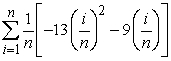
A) Sum =
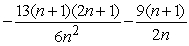 ; limit of sum as
; limit of sum as 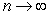 is
is 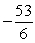

B) Sum =
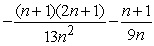 ; limit of sum as
; limit of sum as 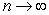 is
is 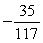

C) Sum =
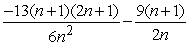 ; limit of sum as
; limit of sum as 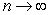 is
is 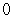

D) Sum =
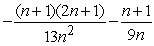 ; limit of sum as
; limit of sum as 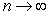 is
is 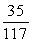


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
36
List the evaluation points corresponding to the midpoint of each subinterval, and evaluate the corresponding Riemann sum. Round the sum to two decimal places. 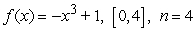
A) Evaluation points: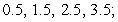 Riemann sum:
Riemann sum: 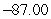
B) Evaluation points: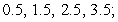 Riemann sum:
Riemann sum: 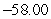
C) Evaluation points: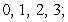 Riemann sum:
Riemann sum: 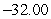
D) Evaluation points: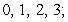 Riemann sum:
Riemann sum: 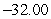
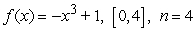
A) Evaluation points:
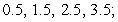 Riemann sum:
Riemann sum: 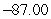
B) Evaluation points:
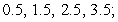 Riemann sum:
Riemann sum: 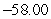
C) Evaluation points:
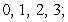 Riemann sum:
Riemann sum: 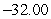
D) Evaluation points:
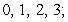 Riemann sum:
Riemann sum: 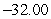

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
37
Compute the sum and the limit of the sum as 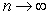 .
. 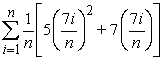
A) Sum =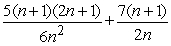 ; limit of sum as
; limit of sum as 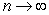 is
is 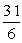
B) Sum =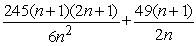 ; limit of sum as
; limit of sum as 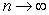 is
is 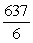

C) Sum =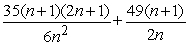 ; limit of sum as
; limit of sum as 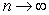 is
is 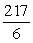
D) Sum =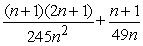 ; limit of sum as
; limit of sum as 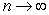 is
is 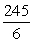

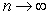 .
. 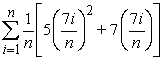
A) Sum =
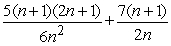 ; limit of sum as
; limit of sum as 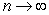 is
is 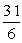
B) Sum =
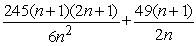 ; limit of sum as
; limit of sum as 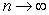 is
is 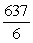

C) Sum =
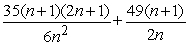 ; limit of sum as
; limit of sum as 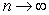 is
is 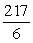
D) Sum =
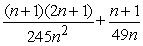 ; limit of sum as
; limit of sum as 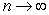 is
is 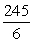


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
38
Translate the following calculation into summation notation and then compute the sum. Round to two decimal places. The square root of the sum of the first 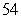 positive integers.
positive integers.
A)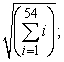 sum =
sum = 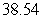
B)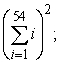 sum =
sum = 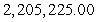
C)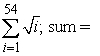
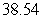
D)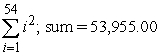
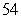 positive integers.
positive integers.A)
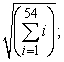 sum =
sum = 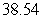
B)
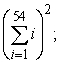 sum =
sum = 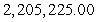
C)
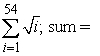
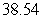
D)
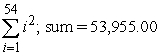

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
39
List the evaluation points corresponding to the midpoint of each subinterval, and evaluate the corresponding Riemann sum. Round the sum to two decimal places. 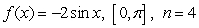
A) Evaluation points: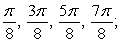 Riemann sum:
Riemann sum: 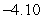
B) Evaluation points: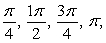 Riemann sum:
Riemann sum: 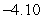
C) Evaluation points: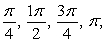 Riemann sum:
Riemann sum: 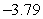
D) Evaluation points: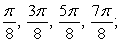 Riemann sum:
Riemann sum: 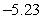
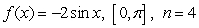
A) Evaluation points:
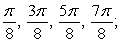 Riemann sum:
Riemann sum: 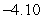
B) Evaluation points:
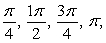 Riemann sum:
Riemann sum: 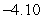
C) Evaluation points:
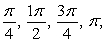 Riemann sum:
Riemann sum: 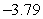
D) Evaluation points:
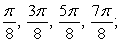 Riemann sum:
Riemann sum: 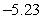

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
40
Use formulas to compute the sum. 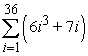
A)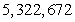
B)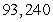
C)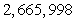
D)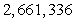
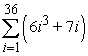
A)
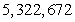
B)
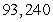
C)
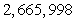
D)
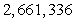

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
41
Use Riemann sums and a limit to compute the exact area under the curve. 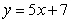 on
on 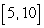
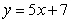 on
on 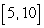

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
42
Write the given (signed) area as an integral or sum of integrals. The area above the 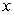 -axis and below
-axis and below 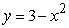
A)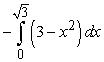
B)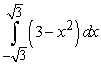
C)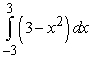
D)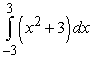
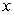 -axis and below
-axis and below 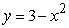
A)
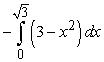
B)
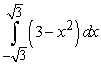
C)
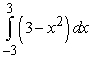
D)
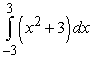

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
43
Approximate the area under the curve on the given interval using 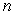 rectangles and midpoint evaluation. Round to three decimal places.
rectangles and midpoint evaluation. Round to three decimal places. 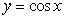 on
on 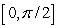 ,
, 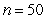
A) 1.000
B) 0.020
C) 0.750
D) 0.667
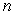 rectangles and midpoint evaluation. Round to three decimal places.
rectangles and midpoint evaluation. Round to three decimal places. 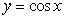 on
on 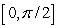 ,
, 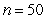
A) 1.000
B) 0.020
C) 0.750
D) 0.667

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
44
Use the Midpoint Rule to estimate the value of the integral (obtain two digits of accuracy). 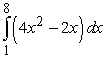
A)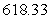
B)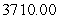
C)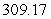
D)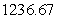
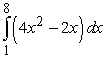
A)
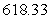
B)
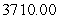
C)
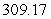
D)
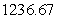

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
45
Write the given (total) area as an integral or sum of integrals. The area between 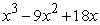 and the
and the 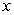 -axis for
-axis for 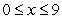 .
.
A)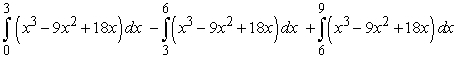
B)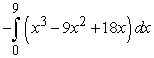
C)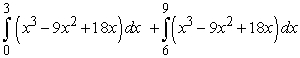
D)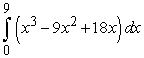
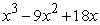 and the
and the 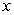 -axis for
-axis for 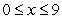 .
.A)
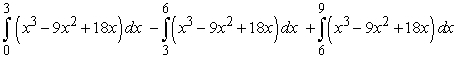
B)
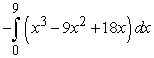
C)
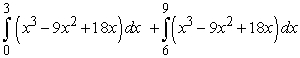
D)
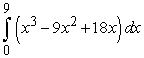

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
46
Approximate the area under the curve on the given interval using 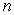 rectangles and midpoint evaluation. Round to three decimal places.
rectangles and midpoint evaluation. Round to three decimal places. 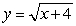 on
on 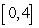 ,
, 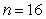
A)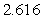
B)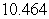
C)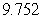
D)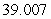
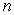 rectangles and midpoint evaluation. Round to three decimal places.
rectangles and midpoint evaluation. Round to three decimal places. 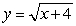 on
on 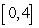 ,
, 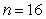
A)
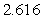
B)
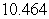
C)
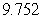
D)
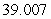

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
47
Write the given (signed) area as an integral or sum of integrals. The area below the 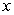 -axis and above
-axis and above 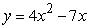
A)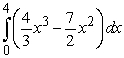
B)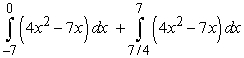
C)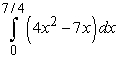
D)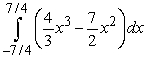
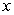 -axis and above
-axis and above 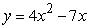
A)
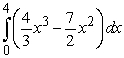
B)
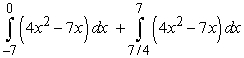
C)
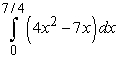
D)
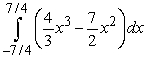

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
48
Use Riemann sums and a limit to compute the exact area under the curve. 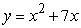 on
on 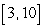
A)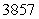
B)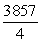
C)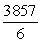
D)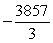
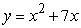 on
on 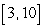
A)
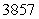
B)
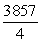
C)
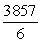
D)
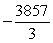

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
49
Use Riemann sums and a limit to compute the exact area under the curve. 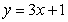 on
on 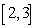
A)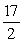
B)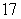
C)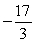
D)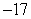
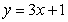 on
on 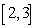
A)
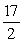
B)
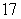
C)
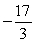
D)
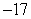

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
50
Use the given velocity function and initial position to estimate the final position s(b). Round to three decimal places, if necessary. 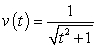 , s(0) = 0, b = 10
, s(0) = 0, b = 10
A) 2.998
B) 2.305
C) 2.308
D) 2.402
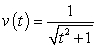 , s(0) = 0, b = 10
, s(0) = 0, b = 10A) 2.998
B) 2.305
C) 2.308
D) 2.402

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
51
Approximate the area under the curve on the given interval using 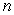 rectangles and right-endpoint evaluation. Round to three decimal places.
rectangles and right-endpoint evaluation. Round to three decimal places. 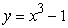 on
on 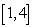 ,
, 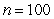
A) 58.704
B) 70.381
C) 63.000
D) 61.698
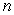 rectangles and right-endpoint evaluation. Round to three decimal places.
rectangles and right-endpoint evaluation. Round to three decimal places. 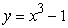 on
on 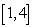 ,
, 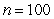
A) 58.704
B) 70.381
C) 63.000
D) 61.698

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
52
Approximate the area under the curve on the given interval using 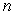 rectangles and right-endpoint evaluation. Round to three decimal places.
rectangles and right-endpoint evaluation. Round to three decimal places. 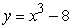 on
on 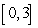 ,
, 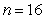
A)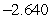
B)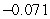
C)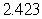
D)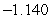
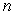 rectangles and right-endpoint evaluation. Round to three decimal places.
rectangles and right-endpoint evaluation. Round to three decimal places. 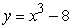 on
on 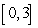 ,
, 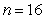
A)
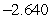
B)
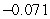
C)
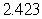
D)
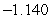

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
53
Use Riemann sums and a limit to compute the exact area under the curve. 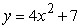 on
on 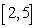
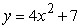 on
on 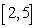

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
54
Use the given function values to estimate the area under the curve using left-endpoint and right-endpoint evaluation. Round to two decimal places. 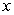 0.0
0.0 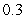
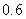
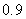
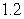
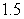
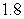
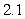
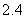
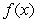
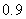
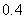
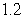
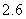
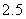
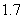
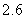
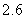
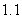

A) Left-endpoint estimate is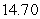 ; right-endpoint estimate is
; right-endpoint estimate is 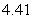
B) Left-endpoint estimate is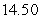 ; right-endpoint estimate is
; right-endpoint estimate is 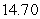
C) Left-endpoint estimate is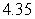 ; right-endpoint estimate is
; right-endpoint estimate is 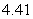
D) Left-endpoint estimate is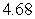 ; right-endpoint estimate is
; right-endpoint estimate is 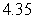
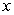 0.0
0.0 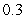
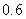
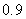
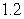
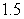
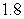
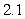
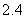
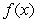
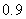
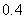
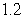
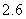
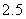
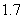
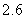
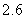
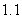

A) Left-endpoint estimate is
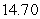 ; right-endpoint estimate is
; right-endpoint estimate is 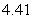
B) Left-endpoint estimate is
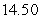 ; right-endpoint estimate is
; right-endpoint estimate is 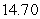
C) Left-endpoint estimate is
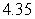 ; right-endpoint estimate is
; right-endpoint estimate is 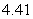
D) Left-endpoint estimate is
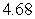 ; right-endpoint estimate is
; right-endpoint estimate is 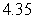

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
55
Approximate the area under the curve on the given interval using 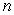 rectangles and left-endpoint evaluation. Round to three decimal places.
rectangles and left-endpoint evaluation. Round to three decimal places. 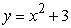 on
on 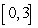 ,
, 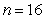
A)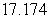
B)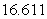
C)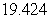
D)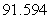
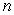 rectangles and left-endpoint evaluation. Round to three decimal places.
rectangles and left-endpoint evaluation. Round to three decimal places. 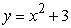 on
on 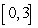 ,
, 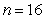
A)
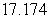
B)
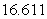
C)
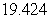
D)
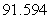

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
56
Give an area interpretation of the integral. 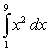
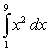

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
57
Use the Midpoint Rule to estimate the value of the integral (obtain two digits of accuracy). 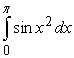
A) 1.20
B)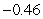
C) 0.77
D) 0.43
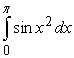
A) 1.20
B)
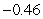
C) 0.77
D) 0.43

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
58
Write the given (total) area as an integral or sum of integrals. The area between 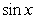 and the
and the 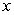 -axis for
-axis for 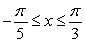 .
.
A)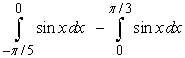
B)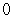
C)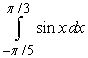
D)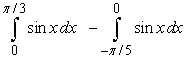
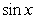 and the
and the 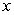 -axis for
-axis for 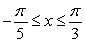 .
.A)
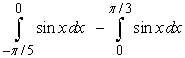
B)
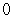
C)
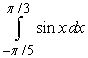
D)
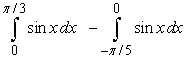

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the integral by computing the limit of Riemann sums. 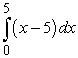
A)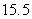
B)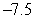
C)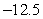
D)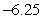
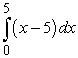
A)
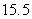
B)
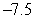
C)
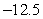
D)
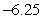

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate the integral by computing the limit of Riemann sums. 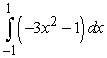
A)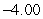
B)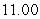
C)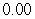
D)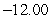
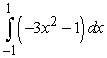
A)
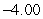
B)
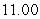
C)
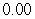
D)
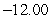

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
61
Use the Integral Mean Value Theorem to estimate the value of the integral. Round to three decimal places, if necessary. 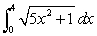
A) between 0 and 36
B) between 1 and 9
C) between 4 and 36
D) between 0 and 9
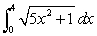
A) between 0 and 36
B) between 1 and 9
C) between 4 and 36
D) between 0 and 9

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
62
Compute the average value of the function on the given interval. 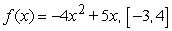
A)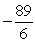
B)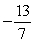
C)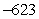
D)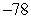
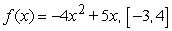
A)
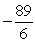
B)
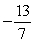
C)
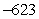
D)
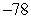

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
63
Use Part I of the Fundamental Theorem of Calculus to compute the integral exactly. 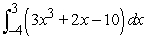
A)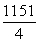
B)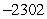
C)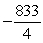
D)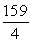

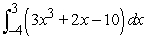
A)
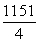
B)
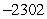
C)
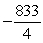
D)
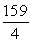


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
64
Write the expression as a single integral. 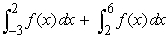
A)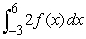
B)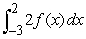
C)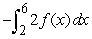
D)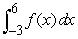
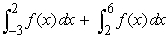
A)
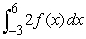
B)
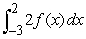
C)
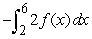
D)
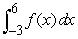

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
65
Use the graph to determine whether 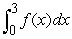 is positive or negative.
is positive or negative. 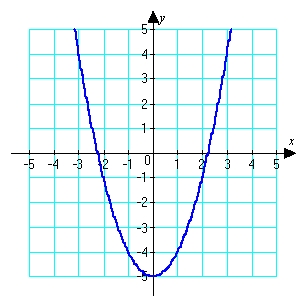
A) Positive
B) Negative
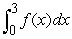 is positive or negative.
is positive or negative. 
A) Positive
B) Negative

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
66
Suppose that, for a particular population of organisms, the birth rate is given by 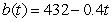 organisms per month and the death rate is given by
organisms per month and the death rate is given by 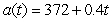 organisms per month. Explain why
organisms per month. Explain why 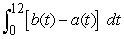 represents the net change in population in the first 12 months. Determine for which values of
represents the net change in population in the first 12 months. Determine for which values of 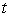 it is true that
it is true that 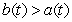 . At which times is the population increasing? Decreasing? Determine the time at which the population reaches a maximum.
. At which times is the population increasing? Decreasing? Determine the time at which the population reaches a maximum.
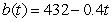 organisms per month and the death rate is given by
organisms per month and the death rate is given by 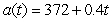 organisms per month. Explain why
organisms per month. Explain why 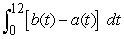 represents the net change in population in the first 12 months. Determine for which values of
represents the net change in population in the first 12 months. Determine for which values of 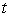 it is true that
it is true that 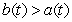 . At which times is the population increasing? Decreasing? Determine the time at which the population reaches a maximum.
. At which times is the population increasing? Decreasing? Determine the time at which the population reaches a maximum.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
67
Use Part 1 of the Fundamental Theorem of Calculus to compute the integral exactly. 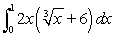
A)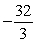
B)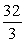
C)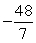
D)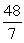
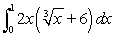
A)
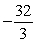
B)
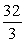
C)
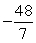
D)
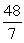

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
68
Use the Integral Mean Value Theorem to estimate the value of the integral. 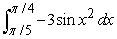
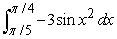

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
69
Use the graph to determine whether 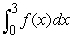 is positive or negative.
is positive or negative. 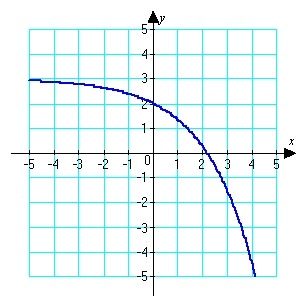
A) Positive
B) Negative
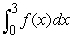 is positive or negative.
is positive or negative. 
A) Positive
B) Negative

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
70
Use Part I of the Fundamental Theorem of Calculus to compute the integral exactly. 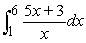
A)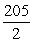
B)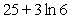
C)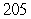
D)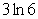
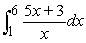
A)
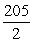
B)
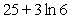
C)
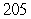
D)
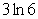

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
71
Use Part I of the Fundamental Theorem of Calculus to compute the integral exactly. 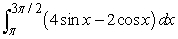
A)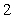
B)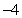
C)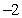
D)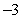
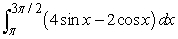
A)
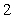
B)
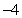
C)
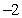
D)
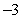

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
72
Use Part I of the Fundamental Theorem of Calculus to compute the integral exactly. 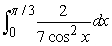
A)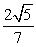
B)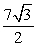
C)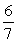
D)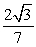

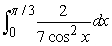
A)
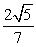
B)
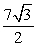
C)
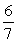
D)
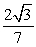


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
73
Sketch the area corresponding to the integral. 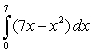
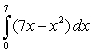

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
74
Find a value of 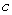 that satisfies the conclusion of the Integral Mean Value Theorem.
that satisfies the conclusion of the Integral Mean Value Theorem. 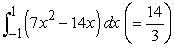
A)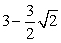
B)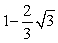

C)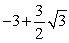
D)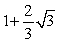
 that satisfies the conclusion of the Integral Mean Value Theorem.
that satisfies the conclusion of the Integral Mean Value Theorem. 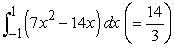
A)
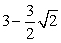
B)
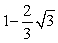

C)
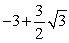
D)
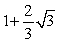

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
75
Compute 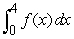 , given
, given 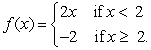
A)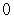
B)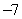
C)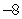
D)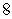
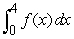 , given
, given 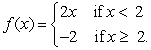
A)
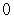
B)
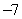
C)
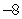
D)
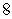

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
76
The impulse-momentum equation states the relationship between a force 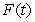 applied to an object of mass
applied to an object of mass 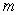 and the resulting change in velocity
and the resulting change in velocity 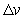 of the object. The equation is
of the object. The equation is 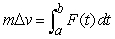 , where
, where 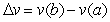 . Suppose that the force of a golf club on a ball is approximately
. Suppose that the force of a golf club on a ball is approximately 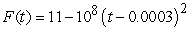 thousand pounds for
thousand pounds for 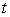 between 0 and
between 0 and 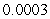 seconds. Using
seconds. Using 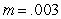 slugs for the mass of a golf ball, estimate the change in velocity
slugs for the mass of a golf ball, estimate the change in velocity 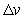 (in ft/s). Round to 2 decimal places.
(in ft/s). Round to 2 decimal places.
A)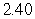 ft/s
ft/s
B)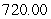 ft/s
ft/s
C)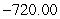 ft/s
ft/s
D)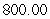 ft/s
ft/s
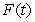 applied to an object of mass
applied to an object of mass 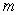 and the resulting change in velocity
and the resulting change in velocity 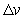 of the object. The equation is
of the object. The equation is 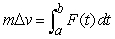 , where
, where 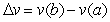 . Suppose that the force of a golf club on a ball is approximately
. Suppose that the force of a golf club on a ball is approximately 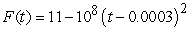 thousand pounds for
thousand pounds for 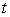 between 0 and
between 0 and 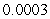 seconds. Using
seconds. Using 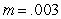 slugs for the mass of a golf ball, estimate the change in velocity
slugs for the mass of a golf ball, estimate the change in velocity 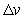 (in ft/s). Round to 2 decimal places.
(in ft/s). Round to 2 decimal places.A)
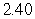 ft/s
ft/sB)
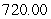 ft/s
ft/sC)
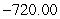 ft/s
ft/sD)
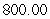 ft/s
ft/s
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
77
Find a value of 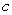 that satisfies the conclusion of the Integral Mean Value Theorem.
that satisfies the conclusion of the Integral Mean Value Theorem. 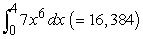
A)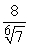
B)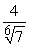
C)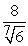
D)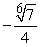
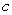 that satisfies the conclusion of the Integral Mean Value Theorem.
that satisfies the conclusion of the Integral Mean Value Theorem. 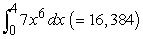
A)
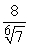
B)
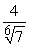
C)
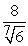
D)
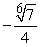

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
78
Write the expression as a single integral. 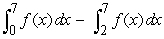
A)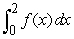
B)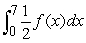
C)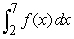
D)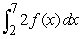
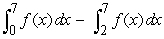
A)
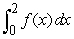
B)
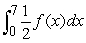
C)
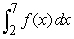
D)
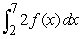

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
79
Use the graph to determine whether 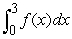 is positive or negative.
is positive or negative. 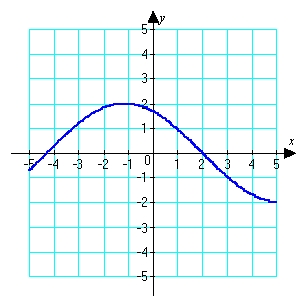
A) Positive
B) Negative
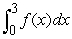 is positive or negative.
is positive or negative. 
A) Positive
B) Negative

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
80
Compute the average value of the function on the given interval. 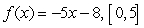
A)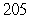
B)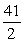
C)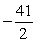
D)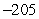
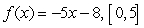
A)
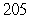
B)
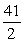
C)
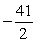
D)
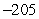

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck


