Exam 5: Integration
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
Use Riemann sums and a limit to compute the exact area under the curve. 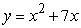 on
on 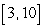
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
C
Use the given substitution to evaluate the indicated integral. 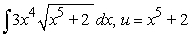
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
C
Evaluate the integral by computing the limit of Riemann sums. 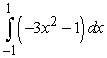
Free
(Multiple Choice)
4.7/5  (26)
(26)
Correct Answer:
A
Write the given (signed) area as an integral or sum of integrals. The area above the 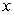 -axis and below
-axis and below 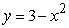
(Multiple Choice)
4.9/5  (40)
(40)
Use Part 1 of the Fundamental Theorem of Calculus to compute the integral exactly. 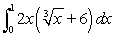
(Multiple Choice)
4.9/5  (45)
(45)
Approximate the area under the curve on the given interval using 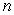 rectangles and left-endpoint evaluation. Round to three decimal places.
rectangles and left-endpoint evaluation. Round to three decimal places. 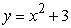 on
on 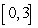 ,
, 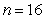
(Multiple Choice)
4.9/5  (35)
(35)
Make the indicated substitution for an unspecified function 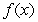 .
. 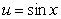 for
for 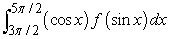
(Multiple Choice)
4.9/5  (38)
(38)
Find the average value of the function on the given interval. 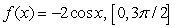
(Multiple Choice)
4.7/5  (34)
(34)
Find the average value of the function on the given interval. 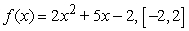
(Multiple Choice)
4.8/5  (27)
(27)
Compute the sum of the form 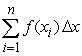 for the given function and
for the given function and 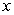 -values, with
-values, with 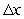 equal to the difference in adjacent
equal to the difference in adjacent 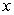 's.
's. 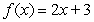 ;
; 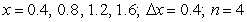
(Multiple Choice)
4.7/5  (22)
(22)
Use the Integral Mean Value Theorem to estimate the value of the integral. Round to three decimal places, if necessary. 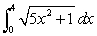
(Multiple Choice)
4.8/5  (31)
(31)
Approximate the given value using Simpson's Rule with 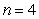 . Round to 3 decimal places.
. Round to 3 decimal places. 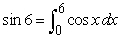
(Multiple Choice)
4.9/5  (30)
(30)
Find the position function 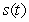 from the given velocity function and initial value. Assume that units are feet and seconds.
from the given velocity function and initial value. Assume that units are feet and seconds. 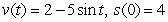
(Multiple Choice)
4.8/5  (45)
(45)
Use the given function values to estimate the area under the curve using left-endpoint and right-endpoint evaluation. Round to two decimal places.  0.0
0.0 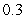
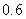
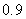
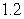
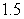
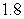
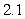
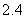
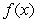
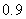
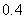
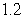
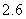
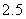
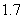
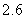
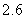
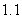

(Multiple Choice)
4.9/5  (33)
(33)
Determine the position function if the acceleration function is 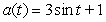 , the initial velocity is
, the initial velocity is 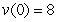 , and the initial position is
, and the initial position is 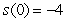 .
.
(Multiple Choice)
5.0/5  (31)
(31)
Showing 1 - 20 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)