Deck 8: Infinite Sequences and Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/341
Play
Full screen (f)
Deck 8: Infinite Sequences and Series
1
Write the fourth-degree Taylor polynomial centered about the origin for the function 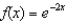 .
.
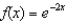 .
.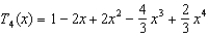
2
Which of the following is the degree 4 Taylor polynomial centered at  for
for  ?
?
1)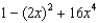 2)
2) 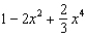 3)
3) 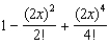 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for  ?
?1)
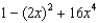 2)
2) 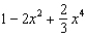 3)
3) 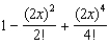 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
G
3
Find the second-degree Taylor polynomial of the function 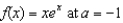 .
.
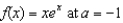 .
.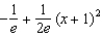
4
According to Taylor's Formula, what is the maximum error possible in the use of the sum 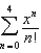 to approximate
to approximate 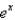 in the interval
in the interval 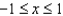 ?
?
A)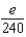 e.
e. 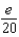 b.
b. 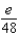 f.
f. 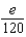 c.
c. 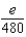 g.
g. 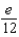 d.
d. 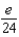 h.
h. 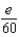
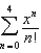 to approximate
to approximate 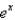 in the interval
in the interval 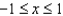 ?
?A)
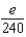 e.
e. 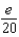 b.
b. 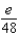 f.
f. 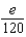 c.
c. 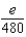 g.
g. 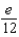 d.
d. 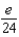 h.
h. 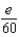

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
5
Estimate the range of values of x for which the approximation ![<strong>Estimate the range of values of x for which the approximation is accurate to within 0.01.</strong> A)[0.68, 1.41] E)[0.95, 1.05] B)[0.61, 1.54] F)[0.80, 1.23] C)[0.995, 1.005] G)[0.980, 1.023] D)[1.51, 2.59] H)[0.89, 1.14]](https://storage.examlex.com/TB2033/11eaa8e2_0da3_dfec_96ab_33a9a51832cc_TB2033_11.jpg) is accurate to within 0.01.
is accurate to within 0.01.
A)[0.68, 1.41]
E)[0.95, 1.05]
B)[0.61, 1.54]
F)[0.80, 1.23]
C)[0.995, 1.005]
G)[0.980, 1.023]
D)[1.51, 2.59]
H)[0.89, 1.14]
![<strong>Estimate the range of values of x for which the approximation is accurate to within 0.01.</strong> A)[0.68, 1.41] E)[0.95, 1.05] B)[0.61, 1.54] F)[0.80, 1.23] C)[0.995, 1.005] G)[0.980, 1.023] D)[1.51, 2.59] H)[0.89, 1.14]](https://storage.examlex.com/TB2033/11eaa8e2_0da3_dfec_96ab_33a9a51832cc_TB2033_11.jpg) is accurate to within 0.01.
is accurate to within 0.01.A)[0.68, 1.41]
E)[0.95, 1.05]
B)[0.61, 1.54]
F)[0.80, 1.23]
C)[0.995, 1.005]
G)[0.980, 1.023]
D)[1.51, 2.59]
H)[0.89, 1.14]

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
6
Give the 4th-degree Taylor polynomial for 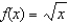 about the point
about the point 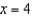 . Using this polynomial, approximate
. Using this polynomial, approximate 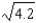 . Give the maximum error for this approximation.
. Give the maximum error for this approximation.
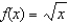 about the point
about the point 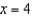 . Using this polynomial, approximate
. Using this polynomial, approximate 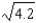 . Give the maximum error for this approximation.
. Give the maximum error for this approximation.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
7
Find an approximation for 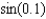 accurate to 6 decimal places.(Note: sin's argument is measured in radians.)
accurate to 6 decimal places.(Note: sin's argument is measured in radians.)
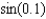 accurate to 6 decimal places.(Note: sin's argument is measured in radians.)
accurate to 6 decimal places.(Note: sin's argument is measured in radians.)
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is the degree 2 Taylor polynomial centered at  for
for 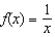 ?
?
1)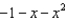 2)
2) 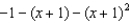 3)
3) 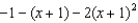 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 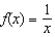 ?
?1)
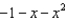 2)
2) 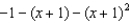 3)
3) 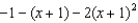 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following is the degree 2 Taylor polynomial centered at  for
for 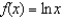 ?
?
1)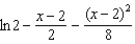 2)
2) 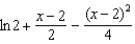 3)
3) 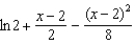 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 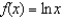 ?
?1)
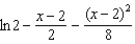 2)
2) 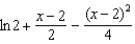 3)
3) 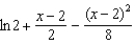 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following is the degree 2 Taylor polynomial centered at  for
for 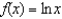 ?
?
1)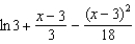 2)
2) 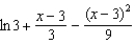 3)
3) 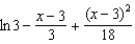 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 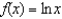 ?
?1)
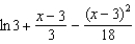 2)
2) 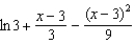 3)
3) 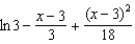 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
11
What is the smallest value of n that will guarantee (according to Taylor's Formula) that the Taylor polynomial 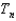 at the number 0 will be within 0.0001 of
at the number 0 will be within 0.0001 of 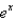 for
for 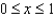 ?
?
A)4
E)7
B)5
F)2
C)8
G)3
D)6
H)9
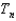 at the number 0 will be within 0.0001 of
at the number 0 will be within 0.0001 of 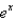 for
for 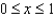 ?
?A)4
E)7
B)5
F)2
C)8
G)3
D)6
H)9

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
12
Estimate the range of values of x for which the approximation 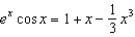 is accurate to within 0.001.
is accurate to within 0.001.
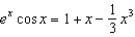 is accurate to within 0.001.
is accurate to within 0.001.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
13
Estimate the range of values of x for which the approximation 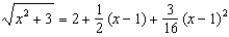 is accurate to within 0.0002.
is accurate to within 0.0002.
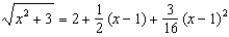 is accurate to within 0.0002.
is accurate to within 0.0002.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
14
Estimate the range of values of x for which the approximation ![<strong>Estimate the range of values of x for which the approximation is accurate to within 0.01.</strong> A)[1.08, 3.20] E)[0.45, 1.78] B)[1.80, 2.20] F)[0.71, 1.33] C)[0.89, 3.56] G)[1.90, 2.10] D)[1.43, 2.66] H)[1.99, 2.01]](https://storage.examlex.com/TB2033/11eaa8e2_0da3_dfed_96ab_830f012e48f0_TB2033_11.jpg) is accurate to within 0.01.
is accurate to within 0.01.
A)[1.08, 3.20]
E)[0.45, 1.78]
B)[1.80, 2.20]
F)[0.71, 1.33]
C)[0.89, 3.56]
G)[1.90, 2.10]
D)[1.43, 2.66]
H)[1.99, 2.01]
![<strong>Estimate the range of values of x for which the approximation is accurate to within 0.01.</strong> A)[1.08, 3.20] E)[0.45, 1.78] B)[1.80, 2.20] F)[0.71, 1.33] C)[0.89, 3.56] G)[1.90, 2.10] D)[1.43, 2.66] H)[1.99, 2.01]](https://storage.examlex.com/TB2033/11eaa8e2_0da3_dfed_96ab_830f012e48f0_TB2033_11.jpg) is accurate to within 0.01.
is accurate to within 0.01.A)[1.08, 3.20]
E)[0.45, 1.78]
B)[1.80, 2.20]
F)[0.71, 1.33]
C)[0.89, 3.56]
G)[1.90, 2.10]
D)[1.43, 2.66]
H)[1.99, 2.01]

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the function 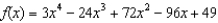 .(a) Find the fourth-degree Taylor polynomial of f at
.(a) Find the fourth-degree Taylor polynomial of f at  .(b) What is the remainder?
.(b) What is the remainder?
(c) What is the absolute minimum value of f, and where does it occur?
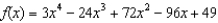 .(a) Find the fourth-degree Taylor polynomial of f at
.(a) Find the fourth-degree Taylor polynomial of f at  .(b) What is the remainder?
.(b) What is the remainder?(c) What is the absolute minimum value of f, and where does it occur?

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
16
Find the second-degree Taylor polynomial for 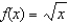 , centered about
, centered about 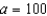 . Also obtain a bound for the error in using this polynomial to approximate
. Also obtain a bound for the error in using this polynomial to approximate 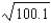 .
.
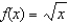 , centered about
, centered about 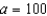 . Also obtain a bound for the error in using this polynomial to approximate
. Also obtain a bound for the error in using this polynomial to approximate 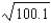 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
17
Find the coefficient of 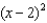 in the Taylor polynomial
in the Taylor polynomial 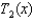 for the function
for the function 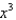 at the number 2.
at the number 2.
A)3
E)2
B)0
F)5
C)1
G)8
D)6
H)4
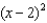 in the Taylor polynomial
in the Taylor polynomial 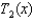 for the function
for the function 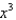 at the number 2.
at the number 2.A)3
E)2
B)0
F)5
C)1
G)8
D)6
H)4

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
18
Find the Taylor polynomial 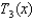 for the function
for the function 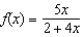 at the point
at the point 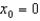 .
.
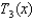 for the function
for the function 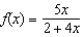 at the point
at the point 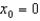 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following is the degree 3 Taylor polynomial centered at  for
for  ?
?
1)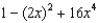 2)
2) 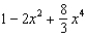 3)
3) 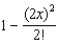 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for  ?
?1)
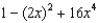 2)
2) 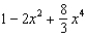 3)
3) 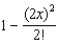 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following is the degree 3 Taylor polynomial centered at  for
for 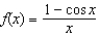 ?
?
1)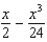 2)
2) 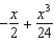 3)
3) 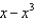 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 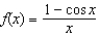 ?
?1)
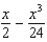 2)
2) 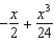 3)
3) 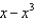 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
21
Find the coefficient of 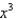 in the Maclaurin series for
in the Maclaurin series for 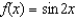 .
.
A)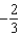 e.
e. 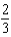 b.
b. 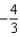 f.
f. 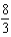 c.
c. 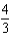 g.
g. 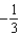 d.
d. 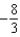 h.
h. 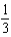
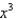 in the Maclaurin series for
in the Maclaurin series for 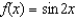 .
.A)
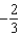 e.
e. 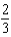 b.
b. 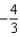 f.
f. 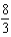 c.
c. 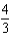 g.
g. 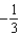 d.
d. 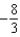 h.
h. 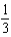

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
22
Find the terms in the Maclaurin series for the function 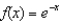 , as far as the term in
, as far as the term in 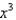 .
.
A)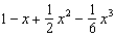 e.
e. 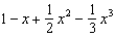 b.
b. 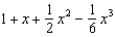 f.
f. 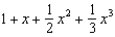 c.
c. 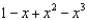 g.
g. 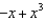 d.
d. 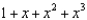 h.
h. 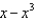
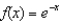 , as far as the term in
, as far as the term in 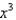 .
.A)
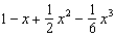 e.
e. 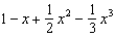 b.
b. 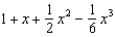 f.
f. 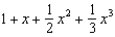 c.
c. 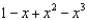 g.
g. 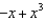 d.
d. 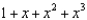 h.
h. 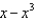

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
23
(a) Find the third-order Taylor polynomial associated with 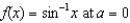 .(b) Use the Taylor polynomial from part (a) to find an approximation of
.(b) Use the Taylor polynomial from part (a) to find an approximation of 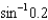 .(c) Compare the value you calculated in part (b) with your calculator's value for
.(c) Compare the value you calculated in part (b) with your calculator's value for 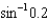
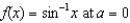 .(b) Use the Taylor polynomial from part (a) to find an approximation of
.(b) Use the Taylor polynomial from part (a) to find an approximation of 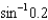 .(c) Compare the value you calculated in part (b) with your calculator's value for
.(c) Compare the value you calculated in part (b) with your calculator's value for 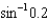

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
24
Find the third-degree Taylor polynomial of the function 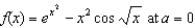 .
.
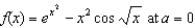 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
25
Find the terms in the Maclaurin series for the function 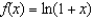 , as far as the term in
, as far as the term in 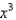 .
.
A)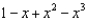 e.
e. 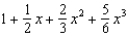 b.
b. 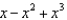 f.
f. 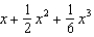 c.
c. 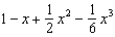 g.
g. 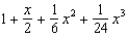 d.
d. 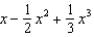 h.
h. 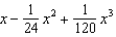
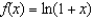 , as far as the term in
, as far as the term in 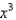 .
.A)
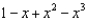 e.
e. 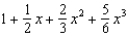 b.
b. 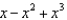 f.
f. 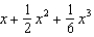 c.
c. 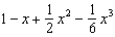 g.
g. 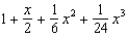 d.
d. 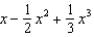 h.
h. 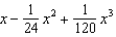

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
26
Find the third-degree Taylor polynomial centered at 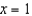 for
for 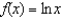 . Use this result to approximate
. Use this result to approximate 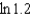 .
.
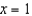 for
for 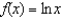 . Use this result to approximate
. Use this result to approximate 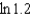 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
27
Given 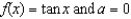 ,
,
(a) calculate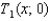 .(b) calculate
.(b) calculate 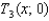 .(c) calculate
.(c) calculate 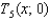 .
.
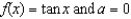 ,
,(a) calculate
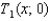 .(b) calculate
.(b) calculate 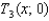 .(c) calculate
.(c) calculate 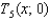 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
28
Find the radius of convergence of the Maclaurin series for 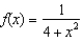 .
.
A)1
E)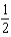 b.
b. 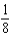 f.4
f.4
C) g.8
g.8
D)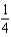 h.2
h.2
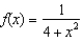 .
.A)1
E)
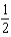 b.
b. 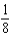 f.4
f.4C)
 g.8
g.8D)
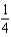 h.2
h.2
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
29
Find the coefficient of 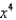 in the Maclaurin series for
in the Maclaurin series for 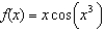 .
.
A)16
E)-16
B)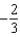 f.
f. 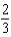 c.3
c.3
G)-3
D)4
H)0
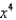 in the Maclaurin series for
in the Maclaurin series for 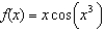 .
.A)16
E)-16
B)
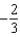 f.
f. 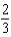 c.3
c.3G)-3
D)4
H)0

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
30
Find the coefficient of 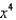 in the Maclaurin series for
in the Maclaurin series for 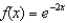 .
.
A)16
E)-16
B)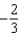 f.
f. 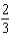 c.3
c.3
G)-3
D)4
H)0
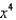 in the Maclaurin series for
in the Maclaurin series for 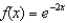 .
.A)16
E)-16
B)
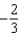 f.
f. 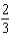 c.3
c.3G)-3
D)4
H)0

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
31
Use the 3rd-degree Taylor polynomial of 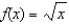 about
about 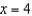 to approximate
to approximate 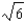 . Use the remainder term to give an upper bound for the error in this approximation.
. Use the remainder term to give an upper bound for the error in this approximation.
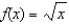 about
about 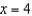 to approximate
to approximate 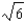 . Use the remainder term to give an upper bound for the error in this approximation.
. Use the remainder term to give an upper bound for the error in this approximation.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
32
Find the coefficient of 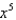 in the Maclaurin series for
in the Maclaurin series for 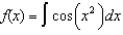 .Note: The series is unique except for the constant of integration.
.Note: The series is unique except for the constant of integration.
A)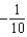 e.
e. 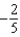 b.
b. 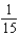 f.
f. 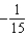 c.
c. 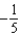 g.
g. 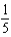 d.
d. 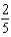 h.
h. 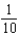
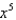 in the Maclaurin series for
in the Maclaurin series for 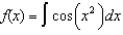 .Note: The series is unique except for the constant of integration.
.Note: The series is unique except for the constant of integration.A)
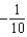 e.
e. 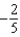 b.
b. 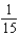 f.
f. 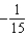 c.
c. 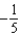 g.
g. 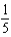 d.
d. 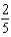 h.
h. 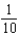

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
33
Write the Taylor polynomial at 0 of degree 4 for 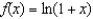 .
.
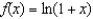 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
34
Find the second-degree Taylor polynomial of the function 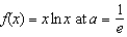 .
.
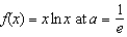 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
35
(a) Use series to compute 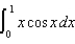 correct to three decimal places.(b) Use integration by parts to compute
correct to three decimal places.(b) Use integration by parts to compute 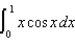 .(c) Compare your answers in parts (a) and (b) above.
.(c) Compare your answers in parts (a) and (b) above.
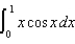 correct to three decimal places.(b) Use integration by parts to compute
correct to three decimal places.(b) Use integration by parts to compute 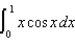 .(c) Compare your answers in parts (a) and (b) above.
.(c) Compare your answers in parts (a) and (b) above.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
36
Use series to compute 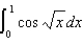 correct to four decimal places.
correct to four decimal places.
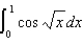 correct to four decimal places.
correct to four decimal places.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
37
Find the third Taylor polynomial associated with 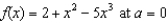 . What is the remainder?
. What is the remainder?
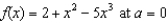 . What is the remainder?
. What is the remainder?
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
38
Find the first four terms in the Maclaurin series for 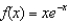 .
.
A)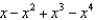 e.
e. 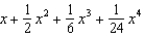 b.
b. 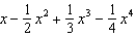 f.
f. 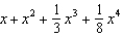 c.
c. 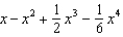 g.
g. 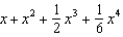 d.
d. 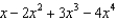 h.
h. 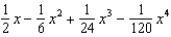
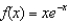 .
.A)
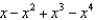 e.
e. 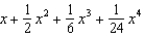 b.
b. 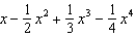 f.
f. 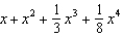 c.
c. 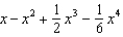 g.
g. 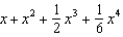 d.
d. 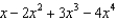 h.
h. 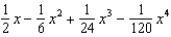

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
39
The first three derivatives of 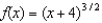 are
are 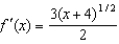 ,
, 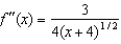 and
and 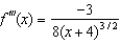 .(a) Give the first four terms of the Taylor series associated with f at
.(a) Give the first four terms of the Taylor series associated with f at  .(b) Give the second-order Taylor polynomial,
.(b) Give the second-order Taylor polynomial, 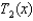 , associated with f at
, associated with f at  .(c) Suppose that
.(c) Suppose that 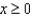 and that
and that 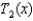 from part (b) is used to approximate
from part (b) is used to approximate 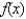 . Prove that the error in this approximation does not exceed
. Prove that the error in this approximation does not exceed  .
.
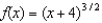 are
are 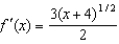 ,
, 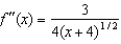 and
and 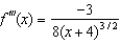 .(a) Give the first four terms of the Taylor series associated with f at
.(a) Give the first four terms of the Taylor series associated with f at  .(b) Give the second-order Taylor polynomial,
.(b) Give the second-order Taylor polynomial, 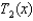 , associated with f at
, associated with f at  .(c) Suppose that
.(c) Suppose that 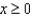 and that
and that 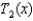 from part (b) is used to approximate
from part (b) is used to approximate 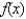 . Prove that the error in this approximation does not exceed
. Prove that the error in this approximation does not exceed  .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
40
Find the third-degree Taylor polynomial of the function 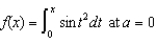 .
.
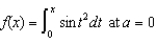 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
41
Give the Taylor series expansion of 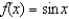 about the point
about the point 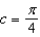 .
.
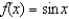 about the point
about the point 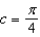 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
42
Find the coefficient of 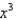 in the binomial series for
in the binomial series for 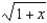 .
.
A)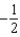 e.
e. 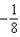 b.
b. 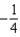 f.
f. 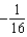 c.
c. 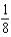 g.
g. 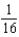 d.
d. 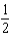 h.
h. 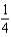
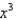 in the binomial series for
in the binomial series for 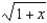 .
.A)
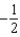 e.
e. 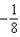 b.
b. 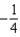 f.
f. 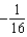 c.
c. 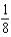 g.
g. 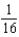 d.
d. 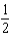 h.
h. 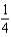

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
43
(a) Express 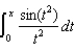 as a Maclaurin series.(b) Evaluate
as a Maclaurin series.(b) Evaluate 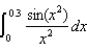 as a series.
as a series.
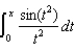 as a Maclaurin series.(b) Evaluate
as a Maclaurin series.(b) Evaluate 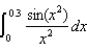 as a series.
as a series.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
44
Express 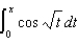 as a Maclaurin Series.
as a Maclaurin Series.
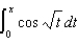 as a Maclaurin Series.
as a Maclaurin Series.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
45
Find the terms of the Maclaurin series for 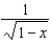 , as far as the term in
, as far as the term in 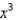 .
.
A)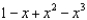 e.
e. 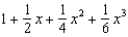 b.
b. 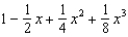 f.
f. 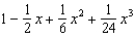 c.
c. 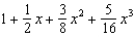 g.
g. 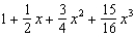 d.
d. 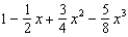 h.
h. 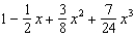
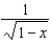 , as far as the term in
, as far as the term in 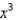 .
.A)
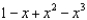 e.
e. 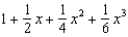 b.
b. 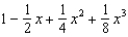 f.
f. 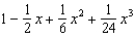 c.
c. 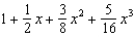 g.
g. 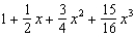 d.
d. 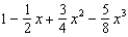 h.
h. 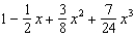

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
46
(a) Express 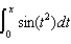 as a Maclaurin series.(b) Evaluate
as a Maclaurin series.(b) Evaluate 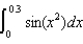 as a series.
as a series.
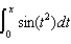 as a Maclaurin series.(b) Evaluate
as a Maclaurin series.(b) Evaluate 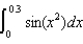 as a series.
as a series.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
47
Find the coefficient of 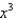 in the binomial series for
in the binomial series for 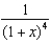 .
.
A)6
E)-20
B)20
F)-12
C)-6
G)10
D)-10
H)12
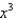 in the binomial series for
in the binomial series for 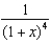 .
.A)6
E)-20
B)20
F)-12
C)-6
G)10
D)-10
H)12

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
48
Find the terms of the Maclaurin series for 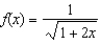 , as far as the term in
, as far as the term in 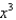 .
.
A)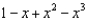 e.
e. 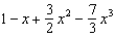 b.
b. 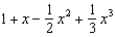 f.
f. 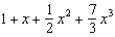 c.
c. 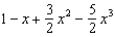 g.
g. 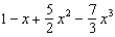 d.
d. 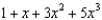 h.
h. 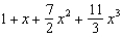
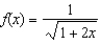 , as far as the term in
, as far as the term in 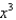 .
.A)
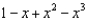 e.
e. 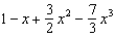 b.
b. 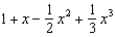 f.
f. 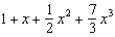 c.
c. 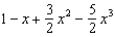 g.
g. 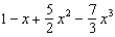 d.
d. 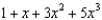 h.
h. 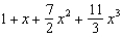

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
49
Find the Taylor series for 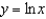 at 2.
at 2.
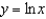 at 2.
at 2.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
50
Express 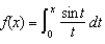 as a Maclaurin Series.
as a Maclaurin Series.
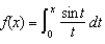 as a Maclaurin Series.
as a Maclaurin Series.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
51
Find the Maclaurin series expansion with  for
for 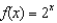 . Use this expansion to approximate
. Use this expansion to approximate 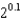 .
.
 for
for 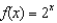 . Use this expansion to approximate
. Use this expansion to approximate 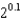 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
52
Find the Maclaurin series expansion for 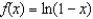 and determine the interval of convergence.
and determine the interval of convergence.
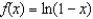 and determine the interval of convergence.
and determine the interval of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
53
Find the Taylor polynomial of degree 4 at 0 for the function defined by 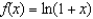 . Then compute the value of
. Then compute the value of 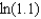 accurate to as many decimal places as the polynomial of degree 4 allows.
accurate to as many decimal places as the polynomial of degree 4 allows.
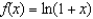 . Then compute the value of
. Then compute the value of 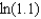 accurate to as many decimal places as the polynomial of degree 4 allows.
accurate to as many decimal places as the polynomial of degree 4 allows.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
54
Express 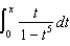 as a Maclaurin Series.
as a Maclaurin Series.
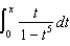 as a Maclaurin Series.
as a Maclaurin Series.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
55
If the Maclaurin series for 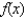 is
is 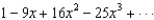 , find
, find 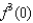 .
.
 is
is 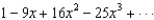 , find
, find 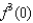 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
56
Find the coefficient of 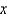 in the binomial series for
in the binomial series for 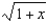 .
.
A)2
E)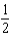 b.-1
b.-1
F)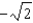 c.1
c.1
G)-2
D)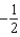 h.
h. 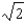
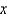 in the binomial series for
in the binomial series for 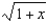 .
.A)2
E)
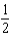 b.-1
b.-1F)
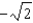 c.1
c.1G)-2
D)
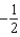 h.
h. 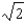

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
57
How many coefficients in the binomial series expansion of 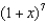 are divisible by 7?
are divisible by 7?
A)0
E)2
B)5
F)6
C)7
G)1
D)3
H)4
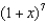 are divisible by 7?
are divisible by 7?A)0
E)2
B)5
F)6
C)7
G)1
D)3
H)4

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
58
Find the coefficient of 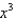 in the binomial series for
in the binomial series for 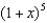 .
.
A)3
E)10
B)6
F)5
C)15
G)16
D)20
H)12
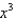 in the binomial series for
in the binomial series for 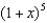 .
.A)3
E)10
B)6
F)5
C)15
G)16
D)20
H)12

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
59
Use the binomial series to expand the function 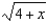 as a power series. Give the coefficient of
as a power series. Give the coefficient of 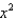 in that series.
in that series.
A)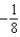 e.
e. 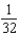 b.
b. 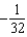 f.
f. 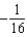 c.
c. 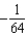 g.
g. 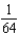 d.
d. 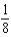 h.
h. 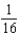
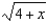 as a power series. Give the coefficient of
as a power series. Give the coefficient of 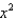 in that series.
in that series.A)
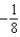 e.
e. 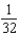 b.
b. 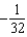 f.
f. 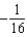 c.
c. 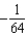 g.
g. 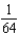 d.
d. 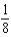 h.
h. 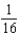

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
60
Find the Taylor series for 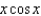 about the origin.
about the origin.
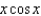 about the origin.
about the origin.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
61
Find the coefficient of 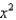 in the Maclaurin series for
in the Maclaurin series for 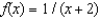 .
.
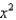 in the Maclaurin series for
in the Maclaurin series for 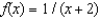 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
62
Use the binomial series to expand 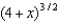 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
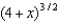 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
63
Find the terms in the power series expansion for the function 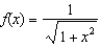 , as far as the term in
, as far as the term in 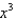 .
.
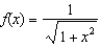 , as far as the term in
, as far as the term in 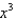 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
64
Find the sum of the series 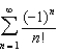 .
.
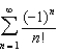 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
65
Find the sum of the series 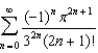 .
.
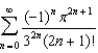 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
66
Use the binomial series to expand 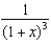 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
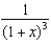 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
67
Which of the following is the power series centered at  for
for 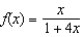 ?
?
1)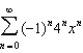 2)
2) 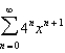 3)
3) 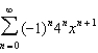 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 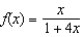 ?
?1)
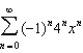 2)
2) 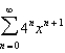 3)
3) 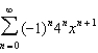 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
68
Which of the following is the power series centered at  for
for 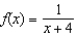 ?
?
1)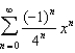 2)
2) 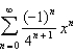 3)
3) 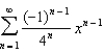 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 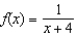 ?
?1)
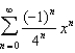 2)
2) 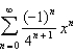 3)
3) 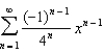 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
69
Use the binomial series formula to obtain the Maclaurin series for 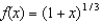 .
.
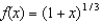 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
70
Which of the following is the power series centered at  for
for 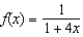 ?
?
1)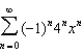 2)
2) 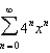 3)
3) 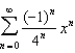 a.None
a.None
E)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3
 for
for 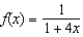 ?
?1)
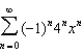 2)
2) 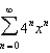 3)
3) 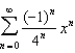 a.None
a.NoneE)1, 2
B)1
F)1, 3
C)2
G)2, 3
D)3
H)1, 2, 3

Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
71
If 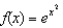 , compute
, compute 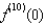 .
.
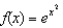 , compute
, compute 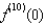 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
72
Use the binomial series to expand 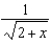 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
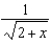 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
73
Find the sum of the series 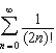 .
.
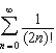 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
74
Let 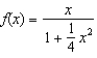 , compute
, compute  .
.
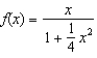 , compute
, compute  .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
75
Find the terms of the Maclaurin series for 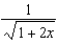 , as far as the term in
, as far as the term in 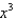 .
.
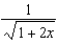 , as far as the term in
, as far as the term in 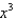 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
76
Find the sum of the series 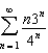 .
.
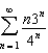 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
77
If 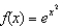 , compute
, compute 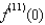 .
.
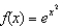 , compute
, compute 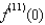 .
.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
78
Use the binomial series to expand 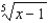 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
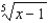 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
79
Use the binomial series to expand 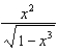 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
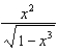 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck
80
Use the binomial series to expand 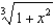 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
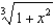 as a power series. State the radius of convergence.
as a power series. State the radius of convergence.
Unlock Deck
Unlock for access to all 341 flashcards in this deck.
Unlock Deck
k this deck


