Deck 7: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/154
Play
Full screen (f)
Deck 7: Differential Equations
1
Suppose that we model populations of predators and preys (in millions) with the system of differential equations: 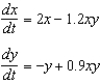 Find the equilibrium solution.
Find the equilibrium solution.
A)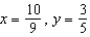 e.
e. 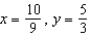 b.
b. 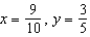 f.
f. 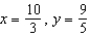 c.
c. 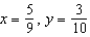 g.
g. 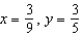 d.
d. 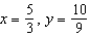 h.
h. 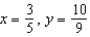
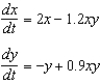 Find the equilibrium solution.
Find the equilibrium solution.A)
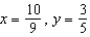 e.
e. 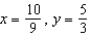 b.
b. 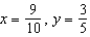 f.
f. 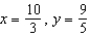 c.
c. 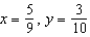 g.
g. 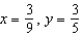 d.
d. 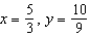 h.
h. 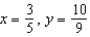
E
2
Suppose a population growth is modeled by the logistic equation 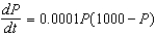 with P(0) = 10. Find the formula for the population after t years.
with P(0) = 10. Find the formula for the population after t years.
A)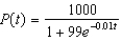 e.
e. 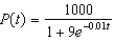 b.
b. 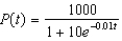 f.
f. 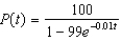 c.
c. 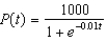 g.
g. 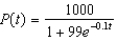 d.
d. 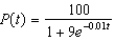 h.
h. 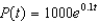
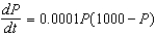 with P(0) = 10. Find the formula for the population after t years.
with P(0) = 10. Find the formula for the population after t years.A)
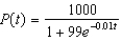 e.
e. 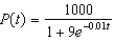 b.
b. 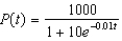 f.
f. 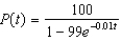 c.
c. 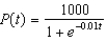 g.
g. 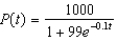 d.
d. 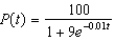 h.
h. 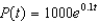
G
3
Suppose a population growth is modeled by the logistic equation 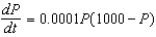 with P(0) = 10. Find the population after 50 years.
with P(0) = 10. Find the population after 50 years.
A)50
E)80
B)500
F)1000
C)600
G)350
D)700
H)300
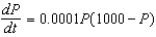 with P(0) = 10. Find the population after 50 years.
with P(0) = 10. Find the population after 50 years.A)50
E)80
B)500
F)1000
C)600
G)350
D)700
H)300
C
4
Consider the predator-prey system 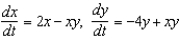 , where x and y are in millions of creatures and t represents time in years.(a) Find equilibrium solutions for this system.(b) Explain why it is reasonable to approximate this predator-prey system as
, where x and y are in millions of creatures and t represents time in years.(a) Find equilibrium solutions for this system.(b) Explain why it is reasonable to approximate this predator-prey system as 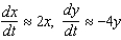 , if the initial conditions are x(0) = 0.001 and y(0) = 0.002.(c) Describe what this approximate system tells about the rate of change of each of the specie populations x(t) and y(t) near (0, 0).(d) Find the solution for the approximate system given in part (b).(e) Sketch x (t) and y (t) as determined in part (d) on the same coordinate plane.(f) Sketch a phase trajectory through (0.001; 0.002) for the predator-prey system. Describe in words what happens to each population of species and the interaction between them.
, if the initial conditions are x(0) = 0.001 and y(0) = 0.002.(c) Describe what this approximate system tells about the rate of change of each of the specie populations x(t) and y(t) near (0, 0).(d) Find the solution for the approximate system given in part (b).(e) Sketch x (t) and y (t) as determined in part (d) on the same coordinate plane.(f) Sketch a phase trajectory through (0.001; 0.002) for the predator-prey system. Describe in words what happens to each population of species and the interaction between them.
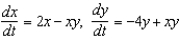 , where x and y are in millions of creatures and t represents time in years.(a) Find equilibrium solutions for this system.(b) Explain why it is reasonable to approximate this predator-prey system as
, where x and y are in millions of creatures and t represents time in years.(a) Find equilibrium solutions for this system.(b) Explain why it is reasonable to approximate this predator-prey system as 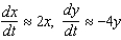 , if the initial conditions are x(0) = 0.001 and y(0) = 0.002.(c) Describe what this approximate system tells about the rate of change of each of the specie populations x(t) and y(t) near (0, 0).(d) Find the solution for the approximate system given in part (b).(e) Sketch x (t) and y (t) as determined in part (d) on the same coordinate plane.(f) Sketch a phase trajectory through (0.001; 0.002) for the predator-prey system. Describe in words what happens to each population of species and the interaction between them.
, if the initial conditions are x(0) = 0.001 and y(0) = 0.002.(c) Describe what this approximate system tells about the rate of change of each of the specie populations x(t) and y(t) near (0, 0).(d) Find the solution for the approximate system given in part (b).(e) Sketch x (t) and y (t) as determined in part (d) on the same coordinate plane.(f) Sketch a phase trajectory through (0.001; 0.002) for the predator-prey system. Describe in words what happens to each population of species and the interaction between them.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose a population growth is modeled by the logistic equation 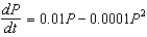 with P(0) = 10. Find the formula for the population after t years.
with P(0) = 10. Find the formula for the population after t years.
A)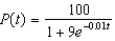 e.
e. 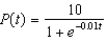 b.
b. 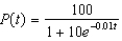 f.
f. 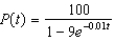 c.
c. 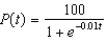 g.
g. 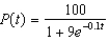 d.
d. 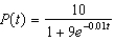 h.
h. 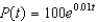
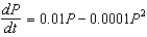 with P(0) = 10. Find the formula for the population after t years.
with P(0) = 10. Find the formula for the population after t years.A)
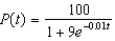 e.
e. 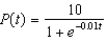 b.
b. 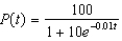 f.
f. 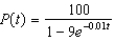 c.
c. 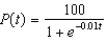 g.
g. 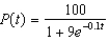 d.
d. 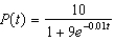 h.
h. 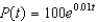

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the following predator-prey system where x and y are in millions of creatures and t represents time in years: 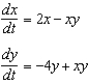 (a) Show that (4, 2) is the nonzero equilibrium solution.(b) Find an expression for
(a) Show that (4, 2) is the nonzero equilibrium solution.(b) Find an expression for 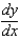 .(c) The direction field for the differential equation is given below:
.(c) The direction field for the differential equation is given below: 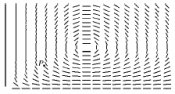 (i) Locate (4, 2) on the graph.(ii) Sketch a rough phase trajectory through P indicated in the graph.(d) With the aid of the phase trajectory, answer the following questions:
(i) Locate (4, 2) on the graph.(ii) Sketch a rough phase trajectory through P indicated in the graph.(d) With the aid of the phase trajectory, answer the following questions:
(i) For the region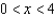 and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(ii) For the region x > 4 and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iii) For the region x > 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iv) For the region 0 < x < 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(e) Suggest a pair of species which might interact in the manner described by this system.
and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(ii) For the region x > 4 and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iii) For the region x > 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iv) For the region 0 < x < 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(e) Suggest a pair of species which might interact in the manner described by this system.
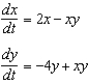 (a) Show that (4, 2) is the nonzero equilibrium solution.(b) Find an expression for
(a) Show that (4, 2) is the nonzero equilibrium solution.(b) Find an expression for 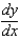 .(c) The direction field for the differential equation is given below:
.(c) The direction field for the differential equation is given below:  (i) Locate (4, 2) on the graph.(ii) Sketch a rough phase trajectory through P indicated in the graph.(d) With the aid of the phase trajectory, answer the following questions:
(i) Locate (4, 2) on the graph.(ii) Sketch a rough phase trajectory through P indicated in the graph.(d) With the aid of the phase trajectory, answer the following questions:(i) For the region
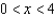 and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(ii) For the region x > 4 and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iii) For the region x > 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iv) For the region 0 < x < 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(e) Suggest a pair of species which might interact in the manner described by this system.
and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(ii) For the region x > 4 and 0 < y < 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iii) For the region x > 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iv) For the region 0 < x < 4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(e) Suggest a pair of species which might interact in the manner described by this system.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
7
A phase portrait of a predator-prey system is given below in which F represents the population of foxes (in thousands) and R the population of rabbits (in thousands). 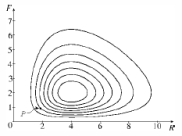 (a) Referring to the graph, what is a reasonable non-zero equilibrium solution for the system?
(a) Referring to the graph, what is a reasonable non-zero equilibrium solution for the system?
(b) Write down a possible system of differential equations which could have been used to produce the given graph.(c) Describe how each population changes as time passes, using the initial condition P indicated on the graph.(d) Use your description in part (c) to make a rough sketch of the graph of R and F as functions of time.
 (a) Referring to the graph, what is a reasonable non-zero equilibrium solution for the system?
(a) Referring to the graph, what is a reasonable non-zero equilibrium solution for the system?(b) Write down a possible system of differential equations which could have been used to produce the given graph.(c) Describe how each population changes as time passes, using the initial condition P indicated on the graph.(d) Use your description in part (c) to make a rough sketch of the graph of R and F as functions of time.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
8
Suppose that we model populations of aphids and ladybugs with the system of differential equations: 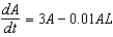
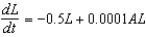 Find the equilibrium solution.
Find the equilibrium solution.
A)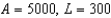 e.
e. 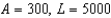 b.
b. 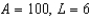 f.
f. 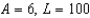 c.
c. 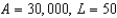 g.
g. 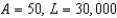 d.
d. 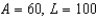 h.
h. 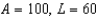
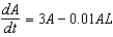
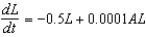 Find the equilibrium solution.
Find the equilibrium solution.A)
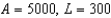 e.
e. 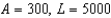 b.
b. 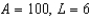 f.
f. 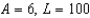 c.
c. 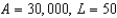 g.
g. 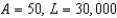 d.
d. 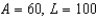 h.
h. 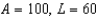

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose a population growth is modeled by the logistic equation 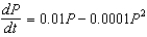 . What is the carrying capacity?
. What is the carrying capacity?
A)90
E)100
B)10
F)60
C)50
G)20
D)1000
H)10,000
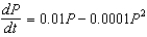 . What is the carrying capacity?
. What is the carrying capacity?A)90
E)100
B)10
F)60
C)50
G)20
D)1000
H)10,000

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose that we model populations (in millions) of predators and preys with the system of differential equations: 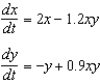 Find the expression for
Find the expression for 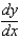 .
.
A)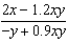 e.
e. 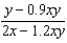 b.
b. 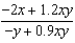 f.
f. 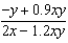 c.
c. 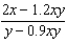 g.
g. 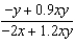 d.
d. 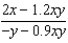 h.
h. 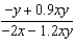
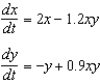 Find the expression for
Find the expression for 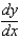 .
.A)
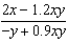 e.
e. 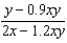 b.
b. 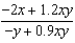 f.
f. 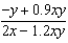 c.
c. 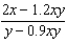 g.
g. 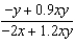 d.
d. 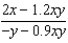 h.
h. 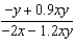

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
11
A predator-prey system is modeled by the system of differential equations 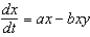 ,
, 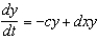 , where a, b, c, and d are positive constants.(a) Which variable, x or y, represents the predator? Defend your choice.(b) Show that the given system of differential equations has the two equilibrium solutions
, where a, b, c, and d are positive constants.(a) Which variable, x or y, represents the predator? Defend your choice.(b) Show that the given system of differential equations has the two equilibrium solutions 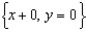 and
and 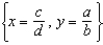 .(c) Explain the significance of each of the equilibrium solutions.
.(c) Explain the significance of each of the equilibrium solutions.
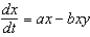 ,
, 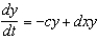 , where a, b, c, and d are positive constants.(a) Which variable, x or y, represents the predator? Defend your choice.(b) Show that the given system of differential equations has the two equilibrium solutions
, where a, b, c, and d are positive constants.(a) Which variable, x or y, represents the predator? Defend your choice.(b) Show that the given system of differential equations has the two equilibrium solutions 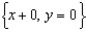 and
and 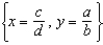 .(c) Explain the significance of each of the equilibrium solutions.
.(c) Explain the significance of each of the equilibrium solutions.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose a population growth is modeled by the logistic differential equation with the carrying capacity 2000 and the relative growth rate k = 0.06 per year. If the initial population is P(0) = 500, and P(10).
A)309
E)308
B)756
F)755
C)310
G)307
D)757
H)800
A)309
E)308
B)756
F)755
C)310
G)307
D)757
H)800

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
13
A rumor tends to spread according to the logistic differential equation 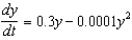 , where y is the number of people in the community who have heard the rumor and t is the time in days.(a) Describe the population for this sociological study.(b) Assume that there were 10 people who knew the rumor at initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to hear the rumor?
, where y is the number of people in the community who have heard the rumor and t is the time in days.(a) Describe the population for this sociological study.(b) Assume that there were 10 people who knew the rumor at initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to hear the rumor?
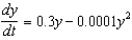 , where y is the number of people in the community who have heard the rumor and t is the time in days.(a) Describe the population for this sociological study.(b) Assume that there were 10 people who knew the rumor at initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to hear the rumor?
, where y is the number of people in the community who have heard the rumor and t is the time in days.(a) Describe the population for this sociological study.(b) Assume that there were 10 people who knew the rumor at initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to hear the rumor?
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose a population growth is modeled by the logistic equation 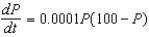 . What is the relative growth rate?
. What is the relative growth rate?
A)0.0001
E)0.0002
B)-0.01
F)-0.02
C)0.001
G)0.002
D)0.01
H)0.02
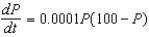 . What is the relative growth rate?
. What is the relative growth rate?A)0.0001
E)0.0002
B)-0.01
F)-0.02
C)0.001
G)0.002
D)0.01
H)0.02

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose a population growth is modeled by the logistic equation 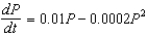 . Solve this differential equation with the initial condition P(0) = 20.
. Solve this differential equation with the initial condition P(0) = 20.
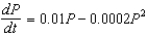 . Solve this differential equation with the initial condition P(0) = 20.
. Solve this differential equation with the initial condition P(0) = 20.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose that we model populations of aphids and ladybugs with the system of differential equations:  Find the expression for
Find the expression for 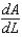 .
.
A)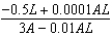 e.
e. 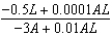 b.
b. 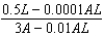 f.
f. 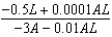 c.
c. 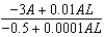 g.
g. 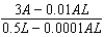 d.
d. 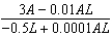 h.
h. 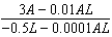
 Find the expression for
Find the expression for 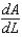 .
.A)
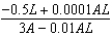 e.
e. 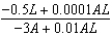 b.
b. 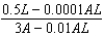 f.
f. 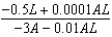 c.
c. 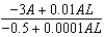 g.
g. 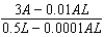 d.
d. 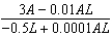 h.
h. 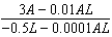

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose that a population of bacteria grows according to the logistic equation 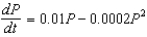 , where P is the population measured in thousands and t is time measured in days.(a) What is the carrying capacity? What is the value of k?
, where P is the population measured in thousands and t is time measured in days.(a) What is the carrying capacity? What is the value of k?
(b) A direction field for this equation is given below. Where are the slopes close to 0? Where are the slope values the largest? Where are the solutions increasing? Where are the solutions decreasing?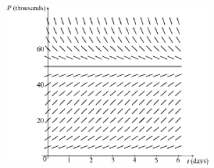 (c) Use the direction field to sketch solutions for initial populations of 10, 30, 50, and 70. What do these solutions have in common? How do they differ? Which solutions have inflection points? At what population levels do they occur?
(c) Use the direction field to sketch solutions for initial populations of 10, 30, 50, and 70. What do these solutions have in common? How do they differ? Which solutions have inflection points? At what population levels do they occur?
(d) What are the equilibrium solutions? How are the other solutions related to these solutions?
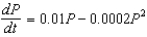 , where P is the population measured in thousands and t is time measured in days.(a) What is the carrying capacity? What is the value of k?
, where P is the population measured in thousands and t is time measured in days.(a) What is the carrying capacity? What is the value of k?(b) A direction field for this equation is given below. Where are the slopes close to 0? Where are the slope values the largest? Where are the solutions increasing? Where are the solutions decreasing?
 (c) Use the direction field to sketch solutions for initial populations of 10, 30, 50, and 70. What do these solutions have in common? How do they differ? Which solutions have inflection points? At what population levels do they occur?
(c) Use the direction field to sketch solutions for initial populations of 10, 30, 50, and 70. What do these solutions have in common? How do they differ? Which solutions have inflection points? At what population levels do they occur?(d) What are the equilibrium solutions? How are the other solutions related to these solutions?

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
18
In each of the given systems, x and y are populations of two different species which are solutions to the differential equations. For each system, describe how the species interact with one another (for example, do they compete for the same resources, or cooperate for mutual benefit?) and suggest a pair of species that might interact in a manner consistent with the given system of equations.(a) 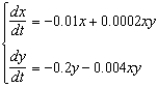 (d)
(d) 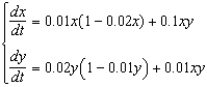 (b)
(b) 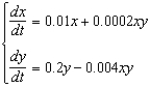 (e)
(e) 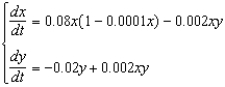 (c)
(c) 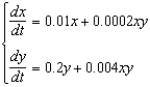 (f)
(f) 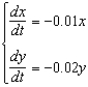
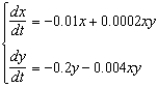 (d)
(d) 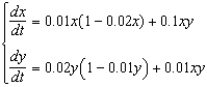 (b)
(b) 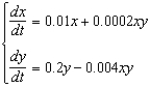 (e)
(e) 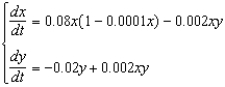 (c)
(c) 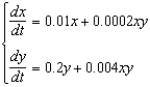 (f)
(f) 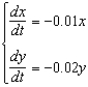

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose a population growth is modeled by the logistic equation 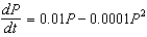 with P(0) = 10. Find the population after 500 years.
with P(0) = 10. Find the population after 500 years.
A)50
E)80
B)94
F)100
C)70
G)35
D)500
H)30
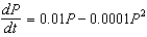 with P(0) = 10. Find the population after 500 years.
with P(0) = 10. Find the population after 500 years.A)50
E)80
B)94
F)100
C)70
G)35
D)500
H)30

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
20
The population of two species is modeled by the system of equations 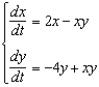 .(a) Find an expression for
.(a) Find an expression for 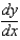 .(b) A possible direction field for the differential equation in part (a) is given below:
.(b) A possible direction field for the differential equation in part (a) is given below: 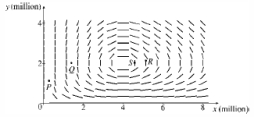 Use this graph to sketch a phase portrait with each of P, Q, R, and S as an initial condition. Describe the behavior of the trajectories near the nonzero equilibrium solutions.(c) Graph x and y as function of t. What happens to the population of the two species as the time t increases without bound?
Use this graph to sketch a phase portrait with each of P, Q, R, and S as an initial condition. Describe the behavior of the trajectories near the nonzero equilibrium solutions.(c) Graph x and y as function of t. What happens to the population of the two species as the time t increases without bound?
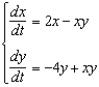 .(a) Find an expression for
.(a) Find an expression for 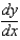 .(b) A possible direction field for the differential equation in part (a) is given below:
.(b) A possible direction field for the differential equation in part (a) is given below:  Use this graph to sketch a phase portrait with each of P, Q, R, and S as an initial condition. Describe the behavior of the trajectories near the nonzero equilibrium solutions.(c) Graph x and y as function of t. What happens to the population of the two species as the time t increases without bound?
Use this graph to sketch a phase portrait with each of P, Q, R, and S as an initial condition. Describe the behavior of the trajectories near the nonzero equilibrium solutions.(c) Graph x and y as function of t. What happens to the population of the two species as the time t increases without bound?
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
21
The radioactive isotope Bismuth-210 has a half-life of 5 days. How many days does it take for 87.5% of a given amount to decay?
A)15 days
E)11 days
B)8 days
F)9 days
C)10 days
G)12 days
D)13 days
H)14 days
A)15 days
E)11 days
B)8 days
F)9 days
C)10 days
G)12 days
D)13 days
H)14 days

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
22
When a child was born, her grandparents deposited $1000 in a saving account at 5% interest compounded continuously. The amount of money after t years is:
A)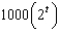 e.
e. 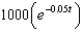 b.
b. 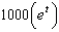 f.
f. 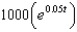 c.
c. 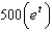 g.
g. 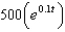 d.
d. 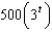 h.
h. 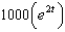
A)
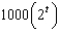 e.
e. 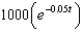 b.
b. 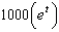 f.
f. 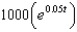 c.
c. 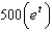 g.
g. 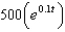 d.
d. 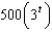 h.
h. 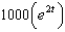

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose that a population grows according to a logistic model.(a) Write the differential equation for this situation with k = 0.01 and carrying capacity of 60 thousand.(b) Solve the differential equation in part (a) with the initial condition t = 0 (hours) and population P = 1 thousand.(c) Find the population for t = 10 hours, t = 100 hours, and t = 1000 hours.(d) After how many hours does the population reach 2 thousand? 30 thousand? 55 thousand?
(e) As the time t increases without bound, what happens to the population?
(f) Sketch the graph of the solution of the differential equation.
(e) As the time t increases without bound, what happens to the population?
(f) Sketch the graph of the solution of the differential equation.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
24
A bacteria culture starts with 200 bacteria and triples in size every half hour. The population of the bacteria after  hours is:
hours is:
A)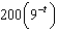 e.
e. 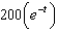 b.
b. 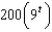 f.
f. 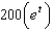 c.
c. 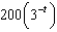 g.
g. 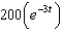 d.
d. 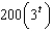 h.
h. 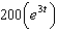
 hours is:
hours is:A)
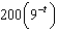 e.
e. 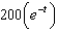 b.
b. 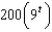 f.
f. 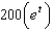 c.
c. 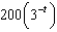 g.
g. 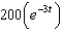 d.
d. 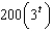 h.
h. 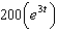

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
25
In a model of epidemics, the number of infected individuals in a population at a time is a solution of the logistic differential equation 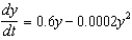 , where y is the number of infected individuals in the community and t is the time in days.(a) Describe the population for this situation.(b) Assume that 10 people were infected at the initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to be infected?
, where y is the number of infected individuals in the community and t is the time in days.(a) Describe the population for this situation.(b) Assume that 10 people were infected at the initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to be infected?
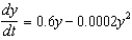 , where y is the number of infected individuals in the community and t is the time in days.(a) Describe the population for this situation.(b) Assume that 10 people were infected at the initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to be infected?
, where y is the number of infected individuals in the community and t is the time in days.(a) Describe the population for this situation.(b) Assume that 10 people were infected at the initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to be infected?
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
26
When a child was born, her grandparents placed $1000 in a savings account at 10% interest compounded continuously, to be withdrawn at age 20 to help pay for college. How much money is in the account at the time of withdrawal?
A)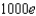 e.
e. 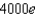 b.
b. 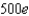 f.
f. 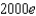 c.
c. 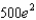 g.
g. 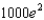 d.
d. 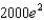 h.
h. 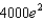
A)
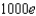 e.
e. 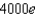 b.
b. 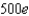 f.
f. 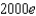 c.
c. 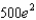 g.
g. 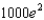 d.
d. 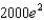 h.
h. 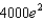

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
27
An object cools at a rate (measured in 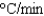 ) equal to
) equal to 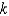 times the difference between its temperature and that of the surrounding air. Suppose the object takes 10 minutes to cool from 60
times the difference between its temperature and that of the surrounding air. Suppose the object takes 10 minutes to cool from 60  C to 40
C to 40  C in a room kept at 20
C in a room kept at 20  C. Find the value of
C. Find the value of 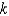 .
.
A)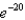 e.
e. 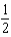 b.
b. 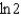 f.
f. 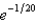 c.
c. 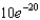 g.
g. 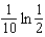 d.
d. 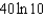 h.
h. 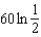
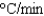 ) equal to
) equal to 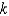 times the difference between its temperature and that of the surrounding air. Suppose the object takes 10 minutes to cool from 60
times the difference between its temperature and that of the surrounding air. Suppose the object takes 10 minutes to cool from 60  C to 40
C to 40  C in a room kept at 20
C in a room kept at 20  C. Find the value of
C. Find the value of 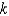 .
.A)
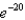 e.
e. 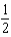 b.
b. 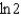 f.
f. 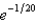 c.
c. 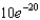 g.
g. 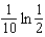 d.
d. 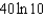 h.
h. 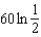

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
28
Radium has a half-life of 1600 years. How many years does it take for 90% of a given amount of radium to decay?
A)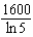 e.
e. 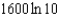 b.
b. 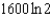 f.
f. 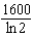 c.
c. 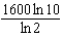 g.
g. 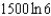 d.
d. 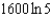 h.
h. 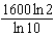
A)
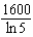 e.
e. 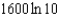 b.
b. 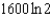 f.
f. 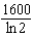 c.
c. 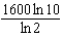 g.
g. 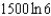 d.
d. 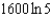 h.
h. 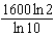

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
29
The radioactive isotope Bismuth-210 has a half-life of 5 days. Suppose we have an initial amount of 100 mg. The amount of Bismuth-210 remaining after 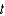 days is
days is
A)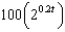 e.
e. 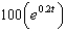 b.
b. 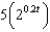 f.
f. 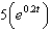 c.
c. 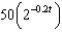 g.
g. 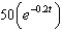 d.
d. 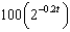 h.
h. 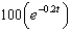
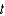 days is
days isA)
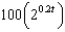 e.
e. 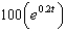 b.
b. 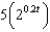 f.
f. 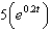 c.
c. 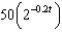 g.
g. 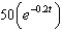 d.
d. 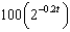 h.
h. 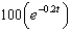

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
30
A bacteria culture starts with 200 bacteria and in 1 hour contains 400 bacteria. How many hours does it take to reach 2000 bacteria?
A)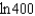 e.
e. 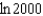 b.
b. 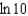 f.
f. 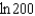 c.
c. 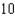 g.
g. 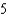 d.
d. 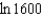 h.
h. 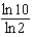
A)
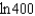 e.
e. 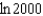 b.
b. 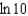 f.
f. 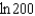 c.
c. 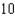 g.
g. 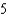 d.
d. 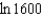 h.
h. 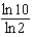

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
31
Assume that a population grows at a rate summarized by the equation ![Assume that a population grows at a rate summarized by the equation , where b and k are positive constants (b > 1), and P is the population at time t. Show that is the general solution for the differential equation (where is the initial population). [Note: This is known as the monomolecular growth curve.]](https://storage.examlex.com/TB2033/11eaa8e2_0e06_7204_96ab_a9568f889a93_TB2033_11.jpg) , where b and k are positive constants (b > 1), and P is the population at time t. Show that
, where b and k are positive constants (b > 1), and P is the population at time t. Show that ![Assume that a population grows at a rate summarized by the equation , where b and k are positive constants (b > 1), and P is the population at time t. Show that is the general solution for the differential equation (where is the initial population). [Note: This is known as the monomolecular growth curve.]](https://storage.examlex.com/TB2033/11eaa8e2_0e06_7205_96ab_d1583844092d_TB2033_11.jpg) is the general solution for the differential equation (where
is the general solution for the differential equation (where ![Assume that a population grows at a rate summarized by the equation , where b and k are positive constants (b > 1), and P is the population at time t. Show that is the general solution for the differential equation (where is the initial population). [Note: This is known as the monomolecular growth curve.]](https://storage.examlex.com/TB2033/11eaa8e2_0e06_9916_96ab_353b7dd44e65_TB2033_11.jpg) is the initial population). [Note: This is known as the monomolecular growth curve.]
is the initial population). [Note: This is known as the monomolecular growth curve.]
![Assume that a population grows at a rate summarized by the equation , where b and k are positive constants (b > 1), and P is the population at time t. Show that is the general solution for the differential equation (where is the initial population). [Note: This is known as the monomolecular growth curve.]](https://storage.examlex.com/TB2033/11eaa8e2_0e06_7204_96ab_a9568f889a93_TB2033_11.jpg) , where b and k are positive constants (b > 1), and P is the population at time t. Show that
, where b and k are positive constants (b > 1), and P is the population at time t. Show that ![Assume that a population grows at a rate summarized by the equation , where b and k are positive constants (b > 1), and P is the population at time t. Show that is the general solution for the differential equation (where is the initial population). [Note: This is known as the monomolecular growth curve.]](https://storage.examlex.com/TB2033/11eaa8e2_0e06_7205_96ab_d1583844092d_TB2033_11.jpg) is the general solution for the differential equation (where
is the general solution for the differential equation (where ![Assume that a population grows at a rate summarized by the equation , where b and k are positive constants (b > 1), and P is the population at time t. Show that is the general solution for the differential equation (where is the initial population). [Note: This is known as the monomolecular growth curve.]](https://storage.examlex.com/TB2033/11eaa8e2_0e06_9916_96ab_353b7dd44e65_TB2033_11.jpg) is the initial population). [Note: This is known as the monomolecular growth curve.]
is the initial population). [Note: This is known as the monomolecular growth curve.]
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
32
Carbon 14, with a half-life of 5700 years, is used to estimate the age of organic materials. What fraction of the original amount of carbon 14 would an object have if it were 2000 years old?
A)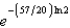 e.
e. 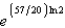 b.
b. 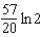 f.
f. 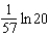 c.
c. 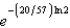 g.
g. 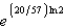 d.
d. 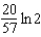 h.
h. 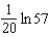
A)
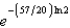 e.
e. 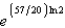 b.
b. 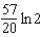 f.
f. 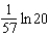 c.
c. 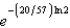 g.
g. 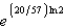 d.
d. 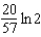 h.
h. 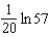

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose that a population, P, grows at a rate given by the equation 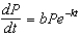 , where P is the population (in thousands) at time t (in hours), and b and k are positive constants.(a) Find the solution to the differential equation when b = 0.04, k = 0.01 and P (0) = 1.(b) Find P (10), P (100), and P (1000).(c) After how many hours does the population reach 2 thousand? 30 thousand? 54 thousand?
, where P is the population (in thousands) at time t (in hours), and b and k are positive constants.(a) Find the solution to the differential equation when b = 0.04, k = 0.01 and P (0) = 1.(b) Find P (10), P (100), and P (1000).(c) After how many hours does the population reach 2 thousand? 30 thousand? 54 thousand?
(d) As time t increases without bound, what happens to the population?
(e) Sketch the graph of the solution of the differential equation.
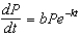 , where P is the population (in thousands) at time t (in hours), and b and k are positive constants.(a) Find the solution to the differential equation when b = 0.04, k = 0.01 and P (0) = 1.(b) Find P (10), P (100), and P (1000).(c) After how many hours does the population reach 2 thousand? 30 thousand? 54 thousand?
, where P is the population (in thousands) at time t (in hours), and b and k are positive constants.(a) Find the solution to the differential equation when b = 0.04, k = 0.01 and P (0) = 1.(b) Find P (10), P (100), and P (1000).(c) After how many hours does the population reach 2 thousand? 30 thousand? 54 thousand?(d) As time t increases without bound, what happens to the population?
(e) Sketch the graph of the solution of the differential equation.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
34
(a) Solve the differential equation 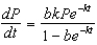 , with b = 2 and k = 0.1, and
, with b = 2 and k = 0.1, and 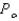 = 1.(b) Sketch a graph of the solution you produced for part (a) and discuss the major characteristics of this monomolecular growth curve.
= 1.(b) Sketch a graph of the solution you produced for part (a) and discuss the major characteristics of this monomolecular growth curve.
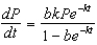 , with b = 2 and k = 0.1, and
, with b = 2 and k = 0.1, and 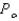 = 1.(b) Sketch a graph of the solution you produced for part (a) and discuss the major characteristics of this monomolecular growth curve.
= 1.(b) Sketch a graph of the solution you produced for part (a) and discuss the major characteristics of this monomolecular growth curve.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose that a certain population grows according to an exponential model.(a) Write the differential equation for this situation with a relative growth rate of k = 0.01. Produce a solution for the initial condition t = 0 (in hours) and population P = 1 (in thousands).(b) Find the population when t = 10 hours, t = 100 hours, and t = 1000 hours.(c) After how many hours does the population reach 2 thousand? 30 thousand? 55 thousand?
(d) As the time t increases without bound, what happens to the population?
(e) Sketch the graph of the solution of the differential equation.
(d) As the time t increases without bound, what happens to the population?
(e) Sketch the graph of the solution of the differential equation.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
36
An outbreak of a previously unknown influenza occurred on the campus of the University of Northern South Dakota at Roscoe during the first semester. Due to the contagious nature of the disease, the campus was quarantined and the disease was allowed to run its course. The table below shows the total number P of infected students for the first four weeks of the outbreak on this campus of 2,500 students.  (a) Find a logistic model for the data. Complete the table with predicted values using this model.(b) Find an exponential model for these data. Complete the table with predicted values using this model.(c) Compare your findings in parts (a) and (b) above. For what values would you consider both models to be a good fit for the data? Which model provides the best fit for the data? Justify your choice.
(a) Find a logistic model for the data. Complete the table with predicted values using this model.(b) Find an exponential model for these data. Complete the table with predicted values using this model.(c) Compare your findings in parts (a) and (b) above. For what values would you consider both models to be a good fit for the data? Which model provides the best fit for the data? Justify your choice.
 (a) Find a logistic model for the data. Complete the table with predicted values using this model.(b) Find an exponential model for these data. Complete the table with predicted values using this model.(c) Compare your findings in parts (a) and (b) above. For what values would you consider both models to be a good fit for the data? Which model provides the best fit for the data? Justify your choice.
(a) Find a logistic model for the data. Complete the table with predicted values using this model.(b) Find an exponential model for these data. Complete the table with predicted values using this model.(c) Compare your findings in parts (a) and (b) above. For what values would you consider both models to be a good fit for the data? Which model provides the best fit for the data? Justify your choice.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
37
The half-life of Carbon 14 is 5700 years. A wooden table is measured with 80% of Carbon 14 compared with newly cut tree. Find the age of the table.
A)2, 933 years
E)13,235 years
B)1,000 years
F)4,200 years
C)500 years
G)1,835 years
D)2,000 years
H)3,000 years
A)2, 933 years
E)13,235 years
B)1,000 years
F)4,200 years
C)500 years
G)1,835 years
D)2,000 years
H)3,000 years

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
38
The following table contains population data for a Minnesota county for the decades from 1900 to 1980: 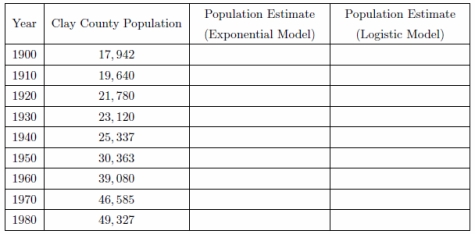 (a) Produce a scatter plot for the data.(b) Find an exponential model using the data from 1900 through 1950.(c) Find a logistic model using the data from 1900 through 1950. (Assume the carrying capacity is 440,000.)
(a) Produce a scatter plot for the data.(b) Find an exponential model using the data from 1900 through 1950.(c) Find a logistic model using the data from 1900 through 1950. (Assume the carrying capacity is 440,000.)
(d) Use your models to estimate the population for 1960, 1970, and 1980. Enter your data in the table provided above.
 (a) Produce a scatter plot for the data.(b) Find an exponential model using the data from 1900 through 1950.(c) Find a logistic model using the data from 1900 through 1950. (Assume the carrying capacity is 440,000.)
(a) Produce a scatter plot for the data.(b) Find an exponential model using the data from 1900 through 1950.(c) Find a logistic model using the data from 1900 through 1950. (Assume the carrying capacity is 440,000.)(d) Use your models to estimate the population for 1960, 1970, and 1980. Enter your data in the table provided above.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
39
A bacteria population grows at a rate proportional to its size. The initial count was 400 and 1600 after 1 hour. In how many minutes does the population double?
A)20
E)40
B)25
F)45
C)30
G)50
D)35
H)55
A)20
E)40
B)25
F)45
C)30
G)50
D)35
H)55

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
40
A bacteria culture starts with 200 bacteria and triples in size every half hour. After 2 hours, how many bacteria are there?
A)17,800
E)19,300
B)16,200
F)14,800
C)23,500
G)15,700
D)24,000
H)21,000
A)17,800
E)19,300
B)16,200
F)14,800
C)23,500
G)15,700
D)24,000
H)21,000

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
41
$2000 is invested at 5% annual interest. Find the value of A(t) at the end of t years if:
(a) the interest compounds monthly.(b) the interest compounds continuously.
(a) the interest compounds monthly.(b) the interest compounds continuously.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
42
An object cools at a rate (in 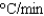 ) equal to
) equal to 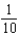 of the difference between its temperature and that of the surrounding air. If a room is kept at 20
of the difference between its temperature and that of the surrounding air. If a room is kept at 20  C and the temperature of the object is 28
C and the temperature of the object is 28  C, what is the temperature of the object 5 minutes later?
C, what is the temperature of the object 5 minutes later?
A)22
E)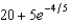 b.24
b.24
F)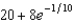 c.
c. 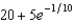 g.
g. 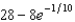 d.
d. 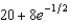 h.
h. 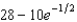
 ) equal to
) equal to 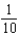 of the difference between its temperature and that of the surrounding air. If a room is kept at 20
of the difference between its temperature and that of the surrounding air. If a room is kept at 20  C and the temperature of the object is 28
C and the temperature of the object is 28  C, what is the temperature of the object 5 minutes later?
C, what is the temperature of the object 5 minutes later?A)22
E)
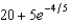 b.24
b.24F)
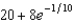 c.
c. 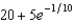 g.
g. 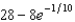 d.
d. 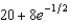 h.
h. 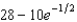

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
43
Assume the half-life of carbon 14 is 5700 years. A wooden statue is measured with 70% of the carbon-14. How old is the statue?

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
44
It takes money 20 years to triple at a certain rate of interest. How long does it take for money to double at this rate?

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
45
The following data approximate the results obtained by subjecting Hela-S cells to 250 kvp x-rays:  Assume that these data fit an exponential model.(a) Find the appropriate exponential model.(b) Add another line to the table using your population model for the given doses of radiation.(c) Compare the model entries to the given data and explain any discrepancy.
Assume that these data fit an exponential model.(a) Find the appropriate exponential model.(b) Add another line to the table using your population model for the given doses of radiation.(c) Compare the model entries to the given data and explain any discrepancy.
 Assume that these data fit an exponential model.(a) Find the appropriate exponential model.(b) Add another line to the table using your population model for the given doses of radiation.(c) Compare the model entries to the given data and explain any discrepancy.
Assume that these data fit an exponential model.(a) Find the appropriate exponential model.(b) Add another line to the table using your population model for the given doses of radiation.(c) Compare the model entries to the given data and explain any discrepancy.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
46
In an experiment, a tissue culture has been subjected to ionizing radiation. It was found that the number A of undamaged cells depends on the exposure time, in hours, according to the formula 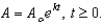 If 5000 cells were present initially and 3000 survived a 2-hour exposure, and the elapsed time of exposure after which only half the original cells survive.
If 5000 cells were present initially and 3000 survived a 2-hour exposure, and the elapsed time of exposure after which only half the original cells survive.
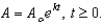 If 5000 cells were present initially and 3000 survived a 2-hour exposure, and the elapsed time of exposure after which only half the original cells survive.
If 5000 cells were present initially and 3000 survived a 2-hour exposure, and the elapsed time of exposure after which only half the original cells survive.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
47
The growth of a population is modeled by the differential equation 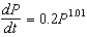 , and the initial population is
, and the initial population is 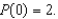 Find
Find 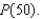 a.37
a.37
E)30
B)90
F)80
C)44,053
G)90,000
D)81,350
H)37,648
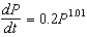 , and the initial population is
, and the initial population is 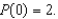 Find
Find 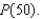 a.37
a.37E)30
B)90
F)80
C)44,053
G)90,000
D)81,350
H)37,648

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the differential equation 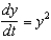 ,
, 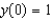 . From your solution, and the value of
. From your solution, and the value of 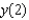 .
.
A)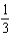 e.
e. 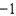 b.1
b.1
F)3
C)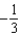 g.
g. 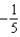 d.
d. 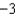 h.
h. 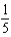
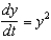 ,
, 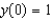 . From your solution, and the value of
. From your solution, and the value of 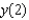 .
.A)
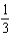 e.
e. 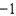 b.1
b.1F)3
C)
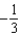 g.
g. 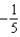 d.
d. 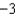 h.
h. 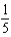

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
49
$2000 is invested at 5% annual interest. Find the value at the end of 18 years if:
(a) the interest compounds monthly.(b) the interest compounds continuously.
(a) the interest compounds monthly.(b) the interest compounds continuously.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
50
In 1970, the Brown County groundhog population was 100. By 1980, there were 900 groundhogs in Brown County. If the rate of population growth of these animals is proportional to the population size, how many groundhogs might one expect to see in 1995?

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
51
In a certain medical treatment, a tracer dye is injected into a human organ to measure its function rate and the rate of change of the amount of dye is proportional to the amount present at any time. If a physician injects 0.5 g of dye and 30 minutes later 0.1 g remains, how much dye will be present in 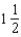 hours?
hours?
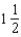 hours?
hours?
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
52
$2000 is invested at 3% annual interest. Find the value at the end of 10 years if:
(a) the interest compounds annually.(b) the interest compounds continuously.
(a) the interest compounds annually.(b) the interest compounds continuously.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
53
A thermometer is taken outside from a room where the temperature is 72  F. Outdoors, the temperature is 48
F. Outdoors, the temperature is 48  F. After one minute, the thermometer reads 55
F. After one minute, the thermometer reads 55  F. After how many minutes does the thermometer read 50
F. After how many minutes does the thermometer read 50  F?
F?
A)2.107
E)2.017
B)1.107
F)1.017
C)3.100
G)3.010
D)1.503
H)1.013
 F. Outdoors, the temperature is 48
F. Outdoors, the temperature is 48  F. After one minute, the thermometer reads 55
F. After one minute, the thermometer reads 55  F. After how many minutes does the thermometer read 50
F. After how many minutes does the thermometer read 50  F?
F?A)2.107
E)2.017
B)1.107
F)1.017
C)3.100
G)3.010
D)1.503
H)1.013

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
54
Find the solution of the initial-value problem 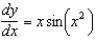 ,
, 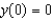 .
.
A)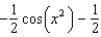 e.
e. 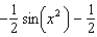 b.
b. 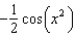 f.
f. 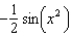 c.
c. 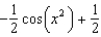 g.
g. 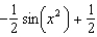 d.
d. 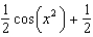 h.
h. 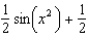
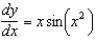 ,
, 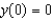 .
.A)
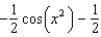 e.
e. 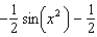 b.
b. 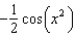 f.
f. 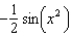 c.
c. 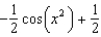 g.
g. 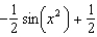 d.
d. 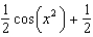 h.
h. 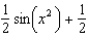

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
55
Assume that the rate of growth of a population of fruit flies is proportional to the size of the population at each instant of time. If 100 fruit flies are present initially and 200 are present after 5 days, how many will be present after 10 days?

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
56
A lettuce leaf collected from the salad bar at the college cafeteria contains 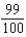 as much carbon-14 as a freshly cut lettuce leaf. How old is it? (Use 5700 years for the half-life of
as much carbon-14 as a freshly cut lettuce leaf. How old is it? (Use 5700 years for the half-life of 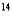 C.)
C.)
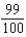 as much carbon-14 as a freshly cut lettuce leaf. How old is it? (Use 5700 years for the half-life of
as much carbon-14 as a freshly cut lettuce leaf. How old is it? (Use 5700 years for the half-life of 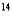 C.)
C.)
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the differential equation 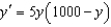 subject to the initial condition
subject to the initial condition 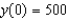 . From your solution, and the value of the limit
. From your solution, and the value of the limit 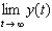 .
.
A)5000
E)200
B)2500
F)20000
C)1000
G)100
D)2000
H)500
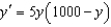 subject to the initial condition
subject to the initial condition 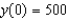 . From your solution, and the value of the limit
. From your solution, and the value of the limit 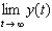 .
.A)5000
E)200
B)2500
F)20000
C)1000
G)100
D)2000
H)500

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
58
$2000 is invested at 3% annual interest. Find the value of A(t) at the end of t years if:
(a) the interest compounds annually.(b) the interest compounds continuously.
(a) the interest compounds annually.(b) the interest compounds continuously.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
59
In an idealized experiment, the following results were obtained for a population of bacteria during a 7 hour period. The initial population is 1000 bacteria.  (a) Identify the period where there is no change in the number of bacteria. (This is called the period of adaptation.)
(a) Identify the period where there is no change in the number of bacteria. (This is called the period of adaptation.)
(b) Identify the period of growth.(c) Assume that the growth rate of bacteria is proportional to the population. Find an exponential model for the data during the period of growth.(d) Add an additional line to the table using your population model to generate the entries for the given time values. Compare these entries with the given data and explain any discrepancy.
 (a) Identify the period where there is no change in the number of bacteria. (This is called the period of adaptation.)
(a) Identify the period where there is no change in the number of bacteria. (This is called the period of adaptation.)(b) Identify the period of growth.(c) Assume that the growth rate of bacteria is proportional to the population. Find an exponential model for the data during the period of growth.(d) Add an additional line to the table using your population model to generate the entries for the given time values. Compare these entries with the given data and explain any discrepancy.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the differential equation 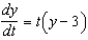 ,
, 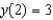 . From your solution, and the value of
. From your solution, and the value of 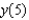 .
.
A)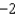 e.
e. 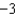 b.2
b.2
F)3
C)5
G)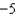 d.0
d.0
H)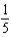
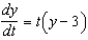 ,
, 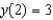 . From your solution, and the value of
. From your solution, and the value of 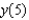 .
.A)
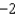 e.
e. 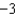 b.2
b.2F)3
C)5
G)
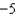 d.0
d.0H)
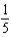

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
61
Find the solution of the initial-value problem 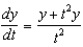 ,
, 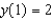 .
.
A)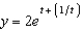 e.
e. 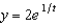 b.
b. 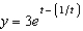 f.
f. 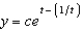 c.
c. 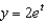 g.
g. 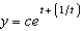 d.
d. 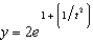 h.
h. 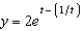
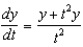 ,
, 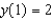 .
.A)
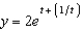 e.
e. 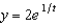 b.
b. 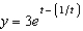 f.
f. 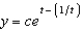 c.
c. 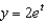 g.
g. 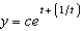 d.
d. 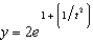 h.
h. 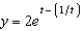

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
62
Find the solution of the initial-value problem 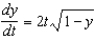 ,
, 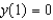 .
.
A)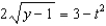 e.
e. 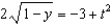 b.
b. 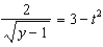 f.
f. 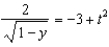 c.
c. 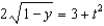 g.
g. 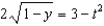 d.
d. 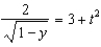 h.
h. 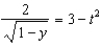
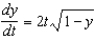 ,
, 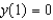 .
.A)
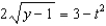 e.
e. 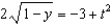 b.
b. 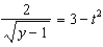 f.
f. 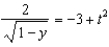 c.
c. 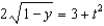 g.
g. 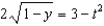 d.
d. 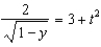 h.
h. 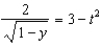

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
63
Find the solution to the differential equation 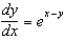 that satisfies the initial condition
that satisfies the initial condition 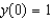 .
.
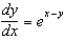 that satisfies the initial condition
that satisfies the initial condition 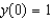 .
.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
64
The graph of a direction field for the differential equation 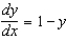 is given below:
is given below: 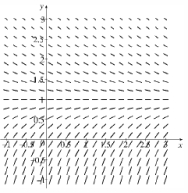 (a) Sketch a solution curve that satisfies the given condition, but without solving the differential equation:
(a) Sketch a solution curve that satisfies the given condition, but without solving the differential equation:
(i)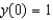 (ii)
(ii) 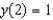 (iii)
(iii) 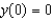 (b) Solve the differential equation for each of the conditions in part (a). Compare your answers to the curves you produced in part (a).(c) What is the relationship between the curves (i) and (ii) in part (a)? Explain why this occurs.
(b) Solve the differential equation for each of the conditions in part (a). Compare your answers to the curves you produced in part (a).(c) What is the relationship between the curves (i) and (ii) in part (a)? Explain why this occurs.
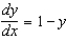 is given below:
is given below:  (a) Sketch a solution curve that satisfies the given condition, but without solving the differential equation:
(a) Sketch a solution curve that satisfies the given condition, but without solving the differential equation:(i)
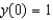 (ii)
(ii) 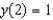 (iii)
(iii) 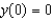 (b) Solve the differential equation for each of the conditions in part (a). Compare your answers to the curves you produced in part (a).(c) What is the relationship between the curves (i) and (ii) in part (a)? Explain why this occurs.
(b) Solve the differential equation for each of the conditions in part (a). Compare your answers to the curves you produced in part (a).(c) What is the relationship between the curves (i) and (ii) in part (a)? Explain why this occurs.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
65
Find the solution of the initial-value problem 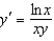 ,
, 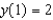 .
.
A)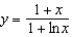 e.
e. 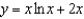 b.
b. 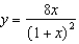 f.
f. 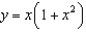 c.
c. 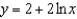 g.
g. 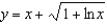 d.
d. 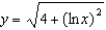 h.
h. 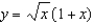
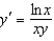 ,
, 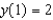 .
.A)
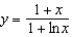 e.
e. 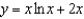 b.
b. 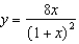 f.
f. 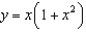 c.
c. 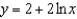 g.
g. 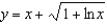 d.
d. 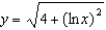 h.
h. 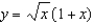

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the initial-value problem 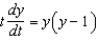 ,
, 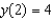 .
.
A)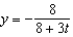 e.
e. 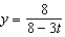 b.
b. 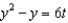 f.
f. 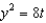 c.
c. 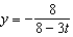 g.
g. 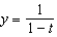 d.
d. 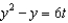 h.
h. 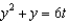
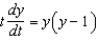 ,
, 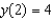 .
.A)
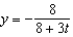 e.
e. 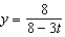 b.
b. 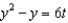 f.
f. 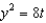 c.
c. 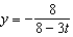 g.
g. 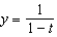 d.
d. 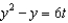 h.
h. 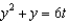

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
67
Find the solution to the differential equation 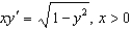 that satisfies the initial condition
that satisfies the initial condition 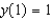 .
.
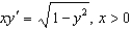 that satisfies the initial condition
that satisfies the initial condition 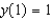 .
.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
68
Find the orthogonal trajectories of the family of curves 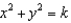 . Then draw several members of each family on the same coordinate plane.
. Then draw several members of each family on the same coordinate plane.
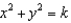 . Then draw several members of each family on the same coordinate plane.
. Then draw several members of each family on the same coordinate plane.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
69
Find the orthogonal trajectories of the family of curves 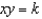 . Then draw several members
. Then draw several members
of each family on the same coordinate plane.
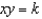 . Then draw several members
. Then draw several membersof each family on the same coordinate plane.

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the initial-value problem 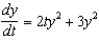 ,
, 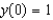 . Then use your solution to evaluate
. Then use your solution to evaluate 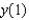 .
.
A)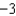 e.0
e.0
B)1
F)3
C)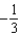 g.
g. 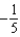 d.
d. 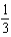 h.
h. 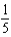
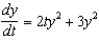 ,
, 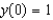 . Then use your solution to evaluate
. Then use your solution to evaluate 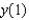 .
.A)
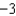 e.0
e.0B)1
F)3
C)
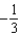 g.
g. 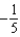 d.
d. 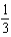 h.
h. 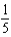

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the initial-value problem 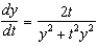 ,
, 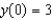 . Then use your solution to evaluate
. Then use your solution to evaluate 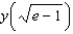 .
.
A)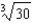 e.
e. 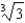 b.
b. 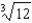 f.
f. 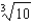 c.
c. 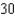 g.12
g.12
D)1
H)27
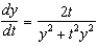 ,
, 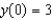 . Then use your solution to evaluate
. Then use your solution to evaluate 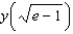 .
.A)
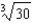 e.
e. 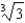 b.
b. 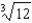 f.
f. 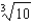 c.
c. 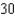 g.12
g.12D)1
H)27

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the initial-value problem 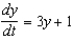 ,
, 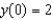 . Then use your solution to evaluate
. Then use your solution to evaluate 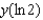 .
.
A)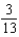 e.
e. 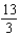 b.
b. 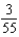 f.
f. 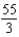 c.
c. 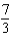 g.
g. 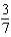 d.
d. 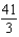 h.9
h.9
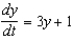 ,
, 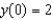 . Then use your solution to evaluate
. Then use your solution to evaluate 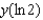 .
.A)
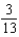 e.
e. 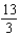 b.
b. 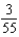 f.
f. 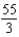 c.
c. 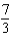 g.
g. 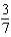 d.
d. 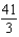 h.9
h.9
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the differential equation 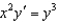 .(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition
.(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition 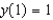 .
.
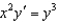 .(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition
.(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition 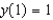 .
.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
74
Find the solution of the initial-value problem 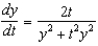 ,
, 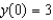 .
.
A)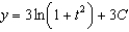 e.
e. 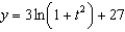 b.
b. 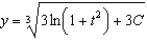 f.
f. 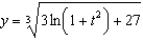 c.
c. 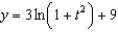 g.
g. 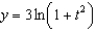 d.
d. 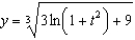 h.
h. 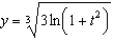
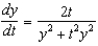 ,
, 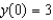 .
.A)
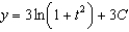 e.
e. 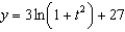 b.
b. 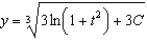 f.
f. 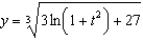 c.
c. 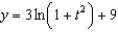 g.
g. 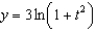 d.
d. 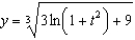 h.
h. 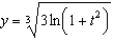

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the differential equation 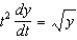 .(a) Find the general solution to the differential equation.(b) Find the solution with the initial-value
.(a) Find the general solution to the differential equation.(b) Find the solution with the initial-value 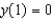 .(c) Find the solution with the initial-value
.(c) Find the solution with the initial-value 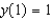 .
.
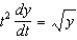 .(a) Find the general solution to the differential equation.(b) Find the solution with the initial-value
.(a) Find the general solution to the differential equation.(b) Find the solution with the initial-value 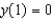 .(c) Find the solution with the initial-value
.(c) Find the solution with the initial-value 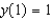 .
.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
76
Find the solution of the initial-value problem 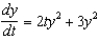 ,
, 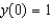 .
.
A)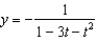 e.
e. 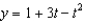 b.
b. 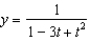 f.
f. 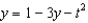 c.
c. 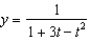 g.
g. 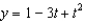 d.
d. 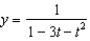 h.
h. 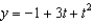
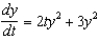 ,
, 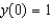 .
.A)
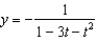 e.
e. 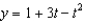 b.
b. 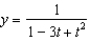 f.
f. 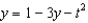 c.
c. 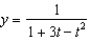 g.
g. 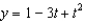 d.
d. 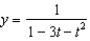 h.
h. 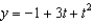

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the differential equation 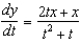 .(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition
.(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition 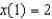 .
.
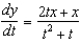 .(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition
.(a) Find the general solution to the differential equation.(b) Find the solution that satisfies the initial condition 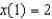 .
.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
78
Find the orthogonal trajectories of the family of curves 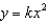 . Then draw several members of each family on the same coordinate plane.
. Then draw several members of each family on the same coordinate plane.
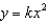 . Then draw several members of each family on the same coordinate plane.
. Then draw several members of each family on the same coordinate plane.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
79
Find the solution of the initial-value problem 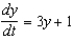 ,
, 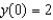 .
.
A)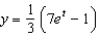 e.
e. 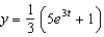 b.
b. 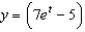 f.
f. 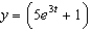 c.
c. 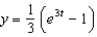 g.
g. 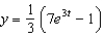 d.
d. 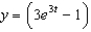 h.
h. 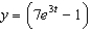
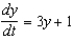 ,
, 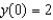 .
.A)
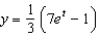 e.
e. 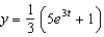 b.
b. 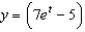 f.
f. 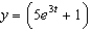 c.
c. 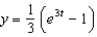 g.
g. 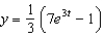 d.
d. 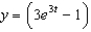 h.
h. 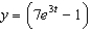

Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck
80
Find the equation of a curve that passes through the point 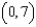 and whose slope at a point
and whose slope at a point 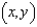 is
is 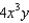 .
.
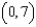 and whose slope at a point
and whose slope at a point 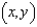 is
is 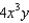 .
.
Unlock Deck
Unlock for access to all 154 flashcards in this deck.
Unlock Deck
k this deck


