Suppose that we model populations of predators and preys (in millions) with the system of differential equations: $\begin{array} { l } \frac { d x } { d t } = 2 x - 1.2 x y \\ \frac { d y } { d t } = - y + 0.9 x y \end{array}$ Find the equilibrium solution.

A) $x = \frac { 10 } { 9 } , y = \frac { 3 } { 5 }$ B) $x = \frac { 9 } { 10 } , y = \frac { 3 } { 5 }$ C) $x = \frac { 5 } { 9 } , y = \frac { 3 } { 10 }$ D) $x = \frac { 5 } { 3 } , y = \frac { 10 } { 9 }$ E) $x = \frac { 10 } { 9 } , y = \frac { 5 } { 3 }$ F) $x = \frac { 10 } { 3 } , y = \frac { 9 } { 5 }$ G) $x = \frac { 3 } { 9 } , y = \frac { 3 } { 5 }$ H) $x = \frac { 3 } { 5 } , y = \frac { 10 } { 9 }$ A) $x = \frac { 10 } { 9 } , y = \frac { 3 } { 5 }$ B) $x = \frac { 9 } { 10 } , y = \frac { 3 } { 5 }$ C) $x = \frac { 5 } { 9 } , y = \frac { 3 } { 10 }$ D) $x = \frac { 5 } { 3 } , y = \frac { 10 } { 9 }$ E) $x = \frac { 10 } { 9 } , y = \frac { 5 } { 3 }$ F) $x = \frac { 10 } { 3 } , y = \frac { 9 } { 5 }$ G) $x = \frac { 3 } { 9 } , y = \frac { 3 } { 5 }$ H) $x = \frac { 3 } { 5 } , y = \frac { 10 } { 9 }$

Exam 7: Differential Equations

Newton's Law of Cooling states that the rate at which a body changes temperature is proportional to the difference between its temperature and the temperature of the surrounding medium. Suppose that a body has an initial temperature of 250 $^\circ$ F and that after one hour the temperature is 200 $^\circ$ F. Assuming that the surrounding air is kept at a constant temperature of 72 $^\circ$ F, determine the temperature of the body at time $t$ .

Free

(Essay)

4.9/5

(43)

Question 1

Correct Answer:

Verified

$\frac { d T } { d t } = k ( T - 72 ) , T ( 0 ) = 250 ^ { \circ } \mathrm { F } , T ( 1 ) = 200 ^ { \circ } \mathrm { F } \Rightarrow T ( t ) = 72 + 178 \left( \frac { 128 } { 178 } \right) ^ { t }$

A direction field for a differential equation is given below: 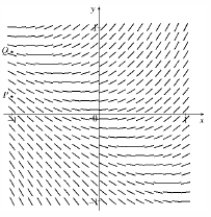(a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

Free

(Essay)

4.8/5

(33)

Question 2

Correct Answer:

Verified

(a) $(a) 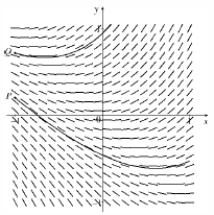(b) It is not autonomous since \frac { d y } { d x } is dependent on both x and y .$
(b) It is not autonomous since $\frac { d y } { d x }$ is dependent on both $x$ and $y$ .

The study of free fall provides one context to consider differential equations. In the simplest case, in the absence of air or other resistance, physicists assume that the rate of change of velocity of a body is constant.(a) Write an equation for $\frac { d v } { d t }$ .(b) As the time $t$ increases without bound, what happens to the velocity $\mathcal { V }$ ?

Free

(Essay)

4.9/5

(39)

Question 3

Correct Answer:

Verified

(a) $\frac { d v } { d t } = a$ where $a$ is a constant.
(b) Since $v ( t ) = a t + v _ { 0 }$ , where $v _ { o }$ is a constant, therefore as $t$ increases without bound, $v ( t )$ will increase without bound.

Suppose $\frac { d y } { d x } = \frac { y ^ { 2 } } { x }$ , $y ( 1 ) = 2$ . Use Euler's method with step size $h = 1$ to approximate $y ( 3 )$ .

(Multiple Choice)

4.9/5

(35)

Question 4

Find the solution of the initial-value problem $\frac { d y } { d t } = 2 t \sqrt { 1 - y }$ , $y ( 1 ) = 0$ .

(Multiple Choice)

4.7/5

(38)

Question 5

Solve the initial-value problem $t \frac { d y } { d t } = y ( y - 1 )$ , $y ( 2 ) = 4$ .

(Multiple Choice)

4.9/5

(27)

Question 6

Solve the initial-value problem $\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }$ , $y ( 0 ) = 1$ . Then use your solution to evaluate $y ( 1 )$ .

(Multiple Choice)

4.9/5

(30)

Question 7

The brakes of a car traveling $60 \mathrm { mph }$ decelerate the car at the rate of 20 ft/s².(a) Determine the differential equation that the position function $y ( t )$ satisfies.(b) What are the initial conditions? (c) If the car is $175 \text { feet }$ from a barrier when the brakes are applied, will it hit the barrier?

(Essay)

4.8/5

(38)

Question 8

Consider the differential equation $x \frac { d y } { d x } - 3 y = 0$ .(a) Sketch the direction field. Indicate where the slopes are $- 1$ , 0, or 1. Draw some other slopes as well.(b) If the point $( 1,2 )$ is on the graph of a solution, use Euler's Method with step size $0.5$ to estimate the value of the solution at $x = 2$ .

(Essay)

4.9/5

(37)

Question 9

Suppose a population growth is modeled by the logistic equation $\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }$ with P(0) = 10. Find the formula for the population after t years.

(Multiple Choice)

4.9/5

(36)

Question 10

Find the orthogonal trajectories of the family of curves $y = k x ^ { 2 }$ . Then draw several members of each family on the same coordinate plane.

(Essay)

4.8/5

(36)

Question 11

A direction field is given below. Which of the following represents its differential equation?

(Multiple Choice)

4.9/5

(36)

Question 12

A predator-prey system is modeled by the system of differential equations $\frac { d x } { d t } = a x - b x y$ , $\frac { d y } { d t } = - c y + d x y$ , where a, b, c, and d are positive constants.(a) Which variable, x or y, represents the predator? Defend your choice.(b) Show that the given system of differential equations has the two equilibrium solutions $\{ x + 0 , y = 0 \}$ and $\left\{ x = \frac { c } { d } , y = \frac { a } { b } \right\}$ .(c) Explain the significance of each of the equilibrium solutions.

(Essay)

4.8/5

(40)

Question 13

The radioactive isotope Bismuth-210 has a half-life of 5 days. Suppose we have an initial amount of 100 mg. The amount of Bismuth-210 remaining after $t$ days is

(Multiple Choice)

4.8/5

(36)

Question 14

Solve the initial-value problem $\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }$ , $y ( 0 ) = 3$ . Then use your solution to evaluate $y ( \sqrt { e - 1 } )$ .

(Multiple Choice)

4.8/5

(37)

Question 15

Consider the differential equation $\frac { d y } { d t } = y - t$ .(a) What are the equilibrium solutions? (b) What are the points in the $t y$ -plane at which the slope of the solution curve is $0$ ? (c) What are the points in the $t y$ -plane at which the slope of the solution curve is $1$ ? (d) What are the points in the $t y$ -plane at which the slope of the solution curve is -1? (e) Use the information from above to sketch the direction field for the given differential equation.

(Essay)

4.8/5

(30)

Question 16

(a) Determine the solution of the differential equation $\frac { d y } { d x } = - y$ where $y ( 0 ) = 1$ .(b) Use the solution $y ( x )$ from part (a) to calculate $y ( 0.4 )$ .(c) Use Euler's Method with the given step sizes to estimate the value of $y ( 0.4 )$ for the equation given in part (a).(i) $h = 0.4$ (ii) $h = 0.2$ (iii) $h = 0.1$ (d) Sketch $y ( x )$ from part (b) and each of the Euler approximations from part (c) on the same set of axes.

(Essay)

4.8/5

(36)

Question 17

The growth of a population is modeled by the differential equation $\frac { d P } { d t } = 0.2 P ^ { 101 }$ , and the initial population is $P ( 0 ) = 2$ Find $P ( 50 )$

(Multiple Choice)

4.9/5

(32)

Question 18

When a child was born, her grandparents deposited $1000 in a saving account at 5% interest compounded continuously. The amount of money after t years is:

(Multiple Choice)

4.9/5

(33)

Question 19

Suppose that we model populations of predators and preys (in millions) with the system of differential equations: =2x-1.2xy =-y+0.9xy Find the equilibrium solution.

(Multiple Choice)

4.9/5

(30)

Question 20

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

Suppose $\frac { d y } { d x } = \frac { y ^ { 2 } } { x }$ , $y ( 1 ) = 2$ . Use Euler's method with step size $h = 1$ to approximate $y ( 3 )$ .

Find the solution of the initial-value problem $\frac { d y } { d t } = 2 t \sqrt { 1 - y }$ , $y ( 1 ) = 0$ .

Solve the initial-value problem $t \frac { d y } { d t } = y ( y - 1 )$ , $y ( 2 ) = 4$ .

Solve the initial-value problem $\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }$ , $y ( 0 ) = 1$ . Then use your solution to evaluate $y ( 1 )$ .

Suppose a population growth is modeled by the logistic equation $\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }$ with P(0) = 10. Find the formula for the population after t years.

Find the orthogonal trajectories of the family of curves $y = k x ^ { 2 }$ . Then draw several members of each family on the same coordinate plane.

A direction field is given below. Which of the following represents its differential equation?

The radioactive isotope Bismuth-210 has a half-life of 5 days. Suppose we have an initial amount of 100 mg. The amount of Bismuth-210 remaining after $t$ days is

Solve the initial-value problem $\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }$ , $y ( 0 ) = 3$ . Then use your solution to evaluate $y ( \sqrt { e - 1 } )$ .

The growth of a population is modeled by the differential equation $\frac { d P } { d t } = 0.2 P ^ { 101 }$ , and the initial population is $P ( 0 ) = 2$ Find $P ( 50 )$

When a child was born, her grandparents deposited $1000 in a saving account at 5% interest compounded continuously. The amount of money after t years is:

Suppose that we model populations of predators and preys (in millions) with the system of differential equations: =2x-1.2xy =-y+0.9xy Find the equilibrium solution.

Functions and Models

Limits and Derivatives

Differentiation Rules

Applications of Differentiation

Integrals

Applications of Integration

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Filters

Exam 7: Differential Equations

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition PPP and initial condition QQQ . (b) Determine whether the differential equation is autonomous. Explain your answer.

Suppose dydx=y2x\frac { d y } { d x } = \frac { y ^ { 2 } } { x }dxdy​=xy2​ , y(1)=2y ( 1 ) = 2y(1)=2 . Use Euler's method with step size h=1h = 1h=1 to approximate y(3)y ( 3 )y(3) .

Find the solution of the initial-value problem dydt=2t1−y\frac { d y } { d t } = 2 t \sqrt { 1 - y }dtdy​=2t1−y​ , y(1)=0y ( 1 ) = 0y(1)=0 .

Solve the initial-value problem tdydt=y(y−1)t \frac { d y } { d t } = y ( y - 1 )tdtdy​=y(y−1) , y(2)=4y ( 2 ) = 4y(2)=4 .

Solve the initial-value problem dydt=2ty2+3y2\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }dtdy​=2ty2+3y2 , y(0)=1y ( 0 ) = 1y(0)=1 . Then use your solution to evaluate y(1)y ( 1 )y(1) .

Suppose a population growth is modeled by the logistic equation dPdt=0.01P−0.0001P2\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }dtdP​=0.01P−0.0001P2 with P(0) = 10. Find the formula for the population after t years.

Find the orthogonal trajectories of the family of curves y=kx2y = k x ^ { 2 }y=kx2 . Then draw several members of each family on the same coordinate plane.

A direction field is given below. Which of the following represents its differential equation?

The radioactive isotope Bismuth-210 has a half-life of 5 days. Suppose we have an initial amount of 100 mg. The amount of Bismuth-210 remaining after ttt days is

Solve the initial-value problem dydt=2ty2+t2y2\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }dtdy​=y2+t2y22t​ , y(0)=3y ( 0 ) = 3y(0)=3 . Then use your solution to evaluate y(e−1)y ( \sqrt { e - 1 } )y(e−1​) .

The growth of a population is modeled by the differential equation dPdt=0.2P101\frac { d P } { d t } = 0.2 P ^ { 101 }dtdP​=0.2P101 , and the initial population is P(0)=2P ( 0 ) = 2P(0)=2 Find P(50)P ( 50 )P(50)

When a child was born, her grandparents deposited $1000 in a saving account at 5% interest compounded continuously. The amount of money after t years is:

Suppose that we model populations of predators and preys (in millions) with the system of differential equations: =2x-1.2xy =-y+0.9xy Find the equilibrium solution.

Functions and Models

Limits and Derivatives

Differentiation Rules

Applications of Differentiation

Integrals

Applications of Integration

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Filters

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

Suppose $\frac { d y } { d x } = \frac { y ^ { 2 } } { x }$ , $y ( 1 ) = 2$ . Use Euler's method with step size $h = 1$ to approximate $y ( 3 )$ .

Find the solution of the initial-value problem $\frac { d y } { d t } = 2 t \sqrt { 1 - y }$ , $y ( 1 ) = 0$ .

Solve the initial-value problem $t \frac { d y } { d t } = y ( y - 1 )$ , $y ( 2 ) = 4$ .

Solve the initial-value problem $\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }$ , $y ( 0 ) = 1$ . Then use your solution to evaluate $y ( 1 )$ .

Suppose a population growth is modeled by the logistic equation $\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }$ with P(0) = 10. Find the formula for the population after t years.

Find the orthogonal trajectories of the family of curves $y = k x ^ { 2 }$ . Then draw several members of each family on the same coordinate plane.

The radioactive isotope Bismuth-210 has a half-life of 5 days. Suppose we have an initial amount of 100 mg. The amount of Bismuth-210 remaining after $t$ days is

Solve the initial-value problem $\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }$ , $y ( 0 ) = 3$ . Then use your solution to evaluate $y ( \sqrt { e - 1 } )$ .

The growth of a population is modeled by the differential equation $\frac { d P } { d t } = 0.2 P ^ { 101 }$ , and the initial population is $P ( 0 ) = 2$ Find $P ( 50 )$