Deck 3: Differentiation Rules
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/248
Play
Full screen (f)
Deck 3: Differentiation Rules
1
Find the linear approximation to at a = 0.
A)1 + x
B)1 + 3x
C)1 - x
D)1 - 3x
E)3 + 3x
F)-3x
G)3 - 3x
H)None of these
A)1 + x
B)1 + 3x
C)1 - x
D)1 - 3x
E)3 + 3x
F)-3x
G)3 - 3x
H)None of these
1 - 3x
2
Find the linear approximation of the function f (x) = at x = 1 and use it to approximate .
A)5.001
B)5.002
C)5.003
D)5.004
E)5.005
F)5.006
G)5.007
H)5.008
A)5.001
B)5.002
C)5.003
D)5.004
E)5.005
F)5.006
G)5.007
H)5.008
5.005
3
Let ![Let (a) Find a linear approximation of f at x = 8: (b) Use this linear approximation to estimate the value of the function at 7, 9, 7.99, and 8.01.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [7; 9]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?](https://storage.examlex.com/TB2033/11eaa8e2_0ef9_d2ab_96ab_cd6aa110e074_TB2033_11.jpg) (a) Find a linear approximation of f at x = 8:
(a) Find a linear approximation of f at x = 8:
(b) Use this linear approximation to estimate the value of the function at 7, 9, 7.99, and 8.01.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [7; 9]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?
![Let (a) Find a linear approximation of f at x = 8: (b) Use this linear approximation to estimate the value of the function at 7, 9, 7.99, and 8.01.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [7; 9]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?](https://storage.examlex.com/TB2033/11eaa8e2_0ef9_d2ab_96ab_cd6aa110e074_TB2033_11.jpg) (a) Find a linear approximation of f at x = 8:
(a) Find a linear approximation of f at x = 8:(b) Use this linear approximation to estimate the value of the function at 7, 9, 7.99, and 8.01.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [7; 9]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?
(a) 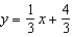 (b), (c)
(b), (c) 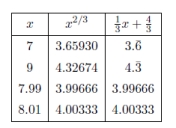 The linear approximation
The linear approximation 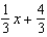 is a good approximation to
is a good approximation to 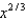 when x is near 8.
when x is near 8.
(d)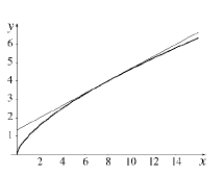
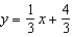 (b), (c)
(b), (c)  The linear approximation
The linear approximation 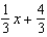 is a good approximation to
is a good approximation to 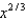 when x is near 8.
when x is near 8.(d)

4
Let , ,and dx = 1. Find the value of the differential dy.
A)2
B)4
C)6
D)8
E)10
F)0.12
G)0
H)
A)2
B)4
C)6
D)8
E)10
F)0.12
G)0
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
5
(a) Find the linearization of the function f (x) = sin x when x = 0.(b) Use these results to approximate sin (0.05) and sin (-0.005).

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
6
Let y = , x = 2, and
x = 1. Find the value of the differential dy.
A)2
B)
C)
D)4
E)
F)
G)3
H)1
x = 1. Find the value of the differential dy.
A)2
B)
C)
D)4
E)
F)
G)3
H)1

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
7
Find the linear approximation of the function f (x) = at x = 1 and use it to approximate .
A)4.888
B)4.948
C)4.958
D)4.968
E)4.978
F)4.988
G)4.998
H)4.9995
A)4.888
B)4.948
C)4.958
D)4.968
E)4.978
F)4.988
G)4.998
H)4.9995

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
8
Use differentials to approximate .
A)4.026
B)4.03
C)4.025
D)4.05
E)4.015
F)0.02498
G)4.0185
H)4.0245
A)4.026
B)4.03
C)4.025
D)4.05
E)4.015
F)0.02498
G)4.0185
H)4.0245

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
9
The diameter of a sphere is measured to be 6 inches with a possible error of 0.05 inches. Use differentials to estimate the maximum error in the calculated volume.

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
10
During the flood of 1997 in Fargo, North Dakota, the Red River of the North rose menacingly during the month of April. Suppose that the official river level at noon on day t is given by the function R(t). We know that R(April 9) = 35.5 feet and (April 9) = 1.
(a) What are the units of (t)?
(b) Construct a linear function to estimate the water level of the Red River for dates near April 9.
(b) to estimate R(April 7) and R(April 11).
(c) Use this model from part
(d) The Red River crested on April 17 at 39.79 feet. What is (April 17)?
(e) If the Red River level on April 22, R(April 22), was 39 feet and (April 22) was -0.3, use a linear model to estimate R(April 26).
(a) What are the units of (t)?
(b) Construct a linear function to estimate the water level of the Red River for dates near April 9.
(b) to estimate R(April 7) and R(April 11).
(c) Use this model from part
(d) The Red River crested on April 17 at 39.79 feet. What is (April 17)?
(e) If the Red River level on April 22, R(April 22), was 39 feet and (April 22) was -0.3, use a linear model to estimate R(April 26).

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
11
Let , x = 3, and x = 1. Find the value of the corresponding change y.
A)4
B)8
C)7
D)2
E)3
F)6
G)1
H)5
A)4
B)8
C)7
D)2
E)3
F)6
G)1
H)5

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
12
Show that for sufficiently small values of h, 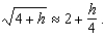
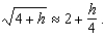

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
13
Find the linear approximation to at
A)-2x + 7
B)
C)
D)
E)
F)
G)
H)
A)-2x + 7
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
14
Use differentials to approximate .
A)5.1
B)5.2
C)5.15
D)5.3
E)5.4
F)5.25
G)5.35
H)5.05
A)5.1
B)5.2
C)5.15
D)5.3
E)5.4
F)5.25
G)5.35
H)5.05

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
15
The period of a pendulum is given by the formula T = 2
, where L is the length of the pendulum in feet, g = 32 ft/ is the acceleration due to gravity, and T is the length of one period in seconds. If the length of the pendulum is measured to be three feet long to within inch, what is the approximate percentage error in the calculated period, T?
, where L is the length of the pendulum in feet, g = 32 ft/ is the acceleration due to gravity, and T is the length of one period in seconds. If the length of the pendulum is measured to be three feet long to within inch, what is the approximate percentage error in the calculated period, T?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
16
Find the linear approximation to at
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
17
The linear approximation of a function is useful only if the change in x is small. Illustrate this fact by approximating 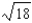 by regarding 18 to be "near" 36 instead of 16.
by regarding 18 to be "near" 36 instead of 16.
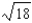 by regarding 18 to be "near" 36 instead of 16.
by regarding 18 to be "near" 36 instead of 16.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
18
Use differentials to approximate the change in the function when x varies from 1 to 1.01.

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
19
A side of a square field is measured to be 144 feet with a possible error of 1 inch.(a) Use differentials to estimate the maximum error in the calculated area of the field.(b) What is the relative error?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
20
The diameter of a sphere is measured to be 6 inches with a possible error of 0.05 inches. Use differentials to estimate the maximum error in the calculated surface area.

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
21
A particle moves along a straight line with equation of motion . Find the value of t at which the acceleration is equal to zero.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
22
A particle moves along a straight line with equation of motion . Find the smallest value of its velocity (for t ≥ 0).
A)
B)-2
C)
D)
E)-3
F)2
G)3
H)
A)
B)-2
C)
D)
E)-3
F)2
G)3
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
23
A stone is thrown into a pond, creating a circular wave whose radius increases at the rate of 1 foot per second. In square feet per second, how fast is the area of the circular ripple increasing 3 seconds after the stone hits the water?
A)
B)2
C)
D)6
E)3
F)
G)
H)
A)
B)2
C)
D)6
E)3
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
24
Profit (in dollars) for a company when x units of a certain product are produced is given by 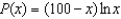 when x > 1.(a) What is the marginal profit (the derivative of the profit function)?
when x > 1.(a) What is the marginal profit (the derivative of the profit function)?
(b) If the current production level is x = 15, is the profit increasing or decreasing?
(c) If the current production level is x = 40, is the profit increasing or decreasing?
(d) At approximately what production level does the profit function reach its maximum value? What is the maximum profit?
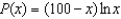 when x > 1.(a) What is the marginal profit (the derivative of the profit function)?
when x > 1.(a) What is the marginal profit (the derivative of the profit function)?(b) If the current production level is x = 15, is the profit increasing or decreasing?
(c) If the current production level is x = 40, is the profit increasing or decreasing?
(d) At approximately what production level does the profit function reach its maximum value? What is the maximum profit?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
25
The cost function of manufacturing x meters of a fabric is 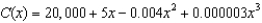 .
.
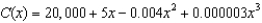 .
.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose that a baseball is tossed straight upward and that its height (in feet) as a function of time (in seconds) is given by the formula h(t) = 128t - 16t2.
(a) Find the instantaneous velocity and acceleration of the baseball at time t.
(b) What is the maximum height attained by the ball?
(c) What is the average velocity of the ball during the time interval from t = 1 to t = 4?
(d) How long does it take before the ball lands?
(e) At what time is the height of the ball 112 feet?
(a) Find the instantaneous velocity and acceleration of the baseball at time t.
(b) What is the maximum height attained by the ball?
(c) What is the average velocity of the ball during the time interval from t = 1 to t = 4?
(d) How long does it take before the ball lands?
(e) At what time is the height of the ball 112 feet?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
27
Show that the rate of change of the circumference of a circle, with respect to the radius of the circle, does not depend on the radius.

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
28
Let ![Let (a) Find a linear approximation of f at x = 1.(b) Use this linear approximation to predict the value of the function at -1, 0, 0.9, 1.1, 2, and 3.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [-1; 3]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?](https://storage.examlex.com/TB2033/11eaa8e2_0efb_cea1_96ab_41bc56631d31_TB2033_11.jpg) (a) Find a linear approximation of f at x = 1.(b) Use this linear approximation to predict the value of the function at -1, 0, 0.9, 1.1, 2, and 3.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [-1; 3]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?
(a) Find a linear approximation of f at x = 1.(b) Use this linear approximation to predict the value of the function at -1, 0, 0.9, 1.1, 2, and 3.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [-1; 3]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?
![Let (a) Find a linear approximation of f at x = 1.(b) Use this linear approximation to predict the value of the function at -1, 0, 0.9, 1.1, 2, and 3.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [-1; 3]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?](https://storage.examlex.com/TB2033/11eaa8e2_0efb_cea1_96ab_41bc56631d31_TB2033_11.jpg) (a) Find a linear approximation of f at x = 1.(b) Use this linear approximation to predict the value of the function at -1, 0, 0.9, 1.1, 2, and 3.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [-1; 3]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?
(a) Find a linear approximation of f at x = 1.(b) Use this linear approximation to predict the value of the function at -1, 0, 0.9, 1.1, 2, and 3.(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval [-1; 3]. What does the graph tell you about the size of the difference between the function values and the linear approximation values?
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
29
The population of a bacteria colony after t hours is given by P(t) = . Find the growth rate of the colony when t = 16 hours.
A)0.087
B)16
C)174
D)700
E)1600
F)2000
G)20,000
H)32,000
A)0.087
B)16
C)174
D)700
E)1600
F)2000
G)20,000
H)32,000

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
30
The mass of a rod varies in such a way that the mass of a piece x meters long, measured from the left end, is kilograms. Find the density in kg/m at the point 2 meters from the left end.
A)1
B)5
C)3
D)4
E)7
F)6
G)2
H)8
A)1
B)5
C)3
D)4
E)7
F)6
G)2
H)8

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
31
If the total cost for producing x units of a particular product is given by C(x), then the average cost of production those x units is given by 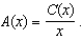 (a) If our cost function is
(a) If our cost function is 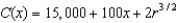 , what value of x will result in the minimum average cost?
, what value of x will result in the minimum average cost?
(b) What is the minimum average cost?
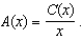 (a) If our cost function is
(a) If our cost function is 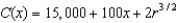 , what value of x will result in the minimum average cost?
, what value of x will result in the minimum average cost?(b) What is the minimum average cost?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
32
A physics experiment involving the acceleration of shuttle on a rail produced the following
data: (a) Make a scatter plot of the data.(b) Fit a quadratic model to the data.(c) Based on your model, what was the initial position of the shuttle?
(a) Make a scatter plot of the data.(b) Fit a quadratic model to the data.(c) Based on your model, what was the initial position of the shuttle?
(d) Using your model, estimate the velocity of the shuttle when t = 0.1 and when t = 0.45 seconds.(e) What is your estimated acceleration of the shuttle when t = 0.1 and when t = 0.45 seconds?
data:
 (a) Make a scatter plot of the data.(b) Fit a quadratic model to the data.(c) Based on your model, what was the initial position of the shuttle?
(a) Make a scatter plot of the data.(b) Fit a quadratic model to the data.(c) Based on your model, what was the initial position of the shuttle?(d) Using your model, estimate the velocity of the shuttle when t = 0.1 and when t = 0.45 seconds.(e) What is your estimated acceleration of the shuttle when t = 0.1 and when t = 0.45 seconds?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
33
Let f (x) = 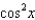 .(a) Find a linear approximation of f at x =
.(a) Find a linear approximation of f at x = 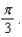 (b) Use this linear approximation to predict the value of the function at
(b) Use this linear approximation to predict the value of the function at 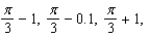 and
and 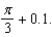 (c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval
(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval 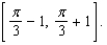 What does the graph tell you about the size of the difference between the function values and the linear approximation values?
What does the graph tell you about the size of the difference between the function values and the linear approximation values?
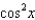 .(a) Find a linear approximation of f at x =
.(a) Find a linear approximation of f at x = 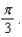 (b) Use this linear approximation to predict the value of the function at
(b) Use this linear approximation to predict the value of the function at 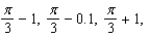 and
and 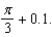 (c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval
(c) Make a table comparing your estimates with the actual function values. Discuss what this tells you about the linear approximation.(d) Graph the original function and its linear approximation over the interval 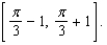 What does the graph tell you about the size of the difference between the function values and the linear approximation values?
What does the graph tell you about the size of the difference between the function values and the linear approximation values?
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
34
The cost function of manufacturing x meters of a fabric is C (x) = 25,000 + 3x - + . Find (5000).
A)58
B)580
C)5.8
D)5800
E)60
F)600
G)6
H)6000
A)58
B)580
C)5.8
D)5800
E)60
F)600
G)6
H)6000

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
35
A particle moves along a straight line with equation of motion . Find the value of t at which the particle reverses its direction.
A)
B)0
C)
D)
E)1
F)2
G)
H)
A)
B)0
C)
D)
E)1
F)2
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
36
The position of a particle is given by the function s(t) = ![The position of a particle is given by the function s(t) = , where t is measured in seconds and s in meters.(a) Find the velocity at time t.(b) When is the particle at rest? (c) When is the particle moving in the positive direction? (d) Draw a diagram to represent the motion of the particle.(e) Find the total distance traveled by the particle during the time interval [1,3].](https://storage.examlex.com/TB2033/11eaa8e2_0efe_b507_96ab_af0eb0a4e1d8_TB2033_11.jpg) , where t is measured in seconds and s in meters.(a) Find the velocity at time t.(b) When is the particle at rest?
, where t is measured in seconds and s in meters.(a) Find the velocity at time t.(b) When is the particle at rest?
(c) When is the particle moving in the positive direction?
(d) Draw a diagram to represent the motion of the particle.(e) Find the total distance traveled by the particle during the time interval [1,3].
![The position of a particle is given by the function s(t) = , where t is measured in seconds and s in meters.(a) Find the velocity at time t.(b) When is the particle at rest? (c) When is the particle moving in the positive direction? (d) Draw a diagram to represent the motion of the particle.(e) Find the total distance traveled by the particle during the time interval [1,3].](https://storage.examlex.com/TB2033/11eaa8e2_0efe_b507_96ab_af0eb0a4e1d8_TB2033_11.jpg) , where t is measured in seconds and s in meters.(a) Find the velocity at time t.(b) When is the particle at rest?
, where t is measured in seconds and s in meters.(a) Find the velocity at time t.(b) When is the particle at rest?(c) When is the particle moving in the positive direction?
(d) Draw a diagram to represent the motion of the particle.(e) Find the total distance traveled by the particle during the time interval [1,3].

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
37
A particle moves along a straight line with equation of motion . Find the instantaneous velocity of the particle at time t = 1.
A)1
B)4
C)0
D)3
E)8
F)6
G)5
H)2
A)1
B)4
C)0
D)3
E)8
F)6
G)5
H)2

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
38
The relationship between the rate of a certain chemical reaction and temperature under certain circumstances is given by grams/sec, where R is the rate of reaction and T is the temperature (in žC).
(a) Find the temperature T at which the reaction rate reaches its maximum.
(b) What is the maximum reaction rate?
(a) Find the temperature T at which the reaction rate reaches its maximum.
(b) What is the maximum reaction rate?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose the amount of a drug left in the body t hours after administration is 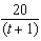 mg. In mg=h, find the rate of decrease of the drug 4 hours after administration.
mg. In mg=h, find the rate of decrease of the drug 4 hours after administration.
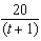 mg. In mg=h, find the rate of decrease of the drug 4 hours after administration.
mg. In mg=h, find the rate of decrease of the drug 4 hours after administration.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
40
Below is a table of the vapor pressure (in kilopascals) of water for various temperatures (in degrees Kelvin): ![Below is a table of the vapor pressure (in kilopascals) of water for various temperatures (in degrees Kelvin): (a) Estimate the rate of change of pressure with respect to temperature on the following intervals: (i) [363, 373] (ii) [333, 343] (iii) [273, 283] (b) Plot the points from the table and fit an appropriate exponential model to these data.(c) From the model in part (b), determine the instantaneous rate of change of pressure with respect to temperature.(d) Is the rate of change of pressure increasing or decreasing with respect to temperature? Justify your answer.](https://storage.examlex.com/TB2033/11eaa8e2_0f00_d80b_96ab_47cada0d5948_TB2033_00.jpg) (a) Estimate the rate of change of pressure with respect to temperature on the following intervals:
(a) Estimate the rate of change of pressure with respect to temperature on the following intervals:
(i) [363, 373]
(ii) [333, 343]
(iii) [273, 283]
(b) Plot the points from the table and fit an appropriate exponential model to these data.(c) From the model in part (b), determine the instantaneous rate of change of pressure with respect to temperature.(d) Is the rate of change of pressure increasing or decreasing with respect to temperature? Justify your answer.
![Below is a table of the vapor pressure (in kilopascals) of water for various temperatures (in degrees Kelvin): (a) Estimate the rate of change of pressure with respect to temperature on the following intervals: (i) [363, 373] (ii) [333, 343] (iii) [273, 283] (b) Plot the points from the table and fit an appropriate exponential model to these data.(c) From the model in part (b), determine the instantaneous rate of change of pressure with respect to temperature.(d) Is the rate of change of pressure increasing or decreasing with respect to temperature? Justify your answer.](https://storage.examlex.com/TB2033/11eaa8e2_0f00_d80b_96ab_47cada0d5948_TB2033_00.jpg) (a) Estimate the rate of change of pressure with respect to temperature on the following intervals:
(a) Estimate the rate of change of pressure with respect to temperature on the following intervals:(i) [363, 373]
(ii) [333, 343]
(iii) [273, 283]
(b) Plot the points from the table and fit an appropriate exponential model to these data.(c) From the model in part (b), determine the instantaneous rate of change of pressure with respect to temperature.(d) Is the rate of change of pressure increasing or decreasing with respect to temperature? Justify your answer.

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
41
Let . Find the value of .
A)
B)ln 3
C)ln
D)1
E)
F)
G)
H)
A)
B)ln 3
C)ln
D)1
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
42
Let . Find the value of .
A)0
B) f.2
C) g.4
D) h.6
E)1
A)0
B) f.2
C) g.4
D) h.6
E)1

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
43
Let . Find the interval on which is concave upward.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
44
Let . Find the value of .
A)0
B)2
C)4
D)6
E)8
F)10
G)12
H)14
A)0
B)2
C)4
D)6
E)8
F)10
G)12
H)14

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
45
Let . Find the value of .
A)2
B)
C)ln
D)
E)
F)
G)
H)
A)2
B)
C)ln
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
46
The following table shows the relationship between pressure (in atmospheres) and volume (in liters) of hydrogen gas at 0 °C. ![The following table shows the relationship between pressure (in atmospheres) and volume (in liters) of hydrogen gas at 0 °C. (a) Find the average rate of change of volume with respect to pressure for the following pressure intervals: (i) [1, 3] (ii) [2, 3] (iii) [4, 5] (b) Plot the data points and fit an appropriate power function to these data.(c) Use the model from part (b) and determine the instantaneous rate of change of volume with respect to pressure.(d) Compare the instantaneous rate at P = 5 with the average rate for [4, 5]. Which is larger? Why is this the case?](https://storage.examlex.com/TB2033/11eaa8e2_0f01_4c43_96ab_fd383b4106a3_TB2033_00.jpg) (a) Find the average rate of change of volume with respect to pressure for the following pressure intervals:
(a) Find the average rate of change of volume with respect to pressure for the following pressure intervals:
(i) [1, 3]
(ii) [2, 3]
(iii) [4, 5]
(b) Plot the data points and fit an appropriate power function to these data.(c) Use the model from part (b) and determine the instantaneous rate of change of volume with respect to pressure.(d) Compare the instantaneous rate at P = 5 with the average rate for [4, 5]. Which is larger? Why is this the case?
![The following table shows the relationship between pressure (in atmospheres) and volume (in liters) of hydrogen gas at 0 °C. (a) Find the average rate of change of volume with respect to pressure for the following pressure intervals: (i) [1, 3] (ii) [2, 3] (iii) [4, 5] (b) Plot the data points and fit an appropriate power function to these data.(c) Use the model from part (b) and determine the instantaneous rate of change of volume with respect to pressure.(d) Compare the instantaneous rate at P = 5 with the average rate for [4, 5]. Which is larger? Why is this the case?](https://storage.examlex.com/TB2033/11eaa8e2_0f01_4c43_96ab_fd383b4106a3_TB2033_00.jpg) (a) Find the average rate of change of volume with respect to pressure for the following pressure intervals:
(a) Find the average rate of change of volume with respect to pressure for the following pressure intervals:(i) [1, 3]
(ii) [2, 3]
(iii) [4, 5]
(b) Plot the data points and fit an appropriate power function to these data.(c) Use the model from part (b) and determine the instantaneous rate of change of volume with respect to pressure.(d) Compare the instantaneous rate at P = 5 with the average rate for [4, 5]. Which is larger? Why is this the case?

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
47
Find the interval on which the graph of is concave upward.
A)(-1, 1)
B)(-1, 2)
C)(-2, 1)
D)(-2, 2)
E)(-1, 3)
F)(-3, 2)
G)(-3, 3)
H)
A)(-1, 1)
B)(-1, 2)
C)(-2, 1)
D)(-2, 2)
E)(-1, 3)
F)(-3, 2)
G)(-3, 3)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
48
Let . Find the value of .
A)2
B)e - 1
C)
D)e + 1
E)e
F)
G)
H)
A)2
B)e - 1
C)
D)e + 1
E)e
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
49
Find an equation of the tangent line to the graph of 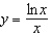 at the point
at the point 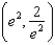 .
.
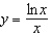 at the point
at the point 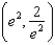 .
.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
50
Let . Find the interval on which is increasing.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
51
Let . Find the value of .
A)2
B)4
C)8
D)16
E)2 + ln 4
F)4 + ln 2
G)8 + 4ln 4
H)16 + 4ln 2
A)2
B)4
C)8
D)16
E)2 + ln 4
F)4 + ln 2
G)8 + 4ln 4
H)16 + 4ln 2

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
52
Find an equation of the tangent line to the graph of 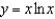 at the point (1, 0).
at the point (1, 0).
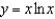 at the point (1, 0).
at the point (1, 0).
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
53
Let . Find the value of .
A)0
B)1
C)2
D)3
E)4
F)5
G)6
H)7
A)0
B)1
C)2
D)3
E)4
F)5
G)6
H)7

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
54
Let . Find the value of .
A)
B)10
C) 10
D)100
E)
100
F)
log10
G)10 log10
H)100 log10
A)
B)10
C) 10
D)100
E)
100
F)
log10
G)10 log10
H)100 log10

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
55
Find the minimum value of .
A)0
B)
C)
D)e
E)
F)
G)1
H)Does not exist
A)0
B)
C)
D)e
E)
F)
G)1
H)Does not exist

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
56
Let . Find the value of .
A)
B)
C)1 + e
D)
E)ln 2
F)1
G)e
H)0
A)
B)
C)1 + e
D)
E)ln 2
F)1
G)e
H)0

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
57
The following table shows the concentration (in mol/L) of a certain chemical in terms of reaction time (in hours) during a decomposition reaction. ![The following table shows the concentration (in mol/L) of a certain chemical in terms of reaction time (in hours) during a decomposition reaction. (a) Find the average rate of change of concentration with respect to time for the following time intervals: (i) [0, 5] (ii) [10, 20] (iii) [30, 50] (b) Plot the points from the table and fit an appropriate exponential model to the data.(c) From your model in part (b), determine the instantaneous rate of change of concentration with respect to time.(d) Is the rate of change of concentration increasing or decreasing with respect to time? Justify your answer.](https://storage.examlex.com/TB2033/11eaa8e2_0f00_ff1f_96ab_afa12ea1ca1f_TB2033_00.jpg) (a) Find the average rate of change of concentration with respect to time for the following time intervals:
(a) Find the average rate of change of concentration with respect to time for the following time intervals:
(i) [0, 5]
(ii) [10, 20]
(iii) [30, 50]
(b) Plot the points from the table and fit an appropriate exponential model to the data.(c) From your model in part (b), determine the instantaneous rate of change of concentration with respect to time.(d) Is the rate of change of concentration increasing or decreasing with respect to time? Justify your answer.
![The following table shows the concentration (in mol/L) of a certain chemical in terms of reaction time (in hours) during a decomposition reaction. (a) Find the average rate of change of concentration with respect to time for the following time intervals: (i) [0, 5] (ii) [10, 20] (iii) [30, 50] (b) Plot the points from the table and fit an appropriate exponential model to the data.(c) From your model in part (b), determine the instantaneous rate of change of concentration with respect to time.(d) Is the rate of change of concentration increasing or decreasing with respect to time? Justify your answer.](https://storage.examlex.com/TB2033/11eaa8e2_0f00_ff1f_96ab_afa12ea1ca1f_TB2033_00.jpg) (a) Find the average rate of change of concentration with respect to time for the following time intervals:
(a) Find the average rate of change of concentration with respect to time for the following time intervals:(i) [0, 5]
(ii) [10, 20]
(iii) [30, 50]
(b) Plot the points from the table and fit an appropriate exponential model to the data.(c) From your model in part (b), determine the instantaneous rate of change of concentration with respect to time.(d) Is the rate of change of concentration increasing or decreasing with respect to time? Justify your answer.

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
58
Let . Find the value of .
A)0
B)1
C)2
D)
E)
F)
G)
H)2
A)0
B)1
C)2
D)
E)
F)
G)
H)2

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
59
Let . Find the value of .
A)0
B)
C)
D)1
E)
F)
G)2
H)3
A)0
B)
C)
D)1
E)
F)
G)2
H)3

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
60
Find the x-coordinate of the point at which the graph of 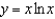 has a horizontal tangent.
has a horizontal tangent.
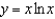 has a horizontal tangent.
has a horizontal tangent.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
61
Find the exact value of .
A)
B)
C)
D)0
E)
F)
G)
H)
A)
B)
C)
D)0
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
62
Differentiate the following functions:
(a)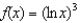 (b)
(b) 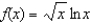 (c)
(c) 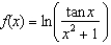
(a)
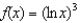 (b)
(b) 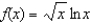 (c)
(c) 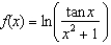

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
63
Find the x-coordinate of the point at which the graph of 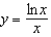 has a horizontal tangent.
has a horizontal tangent.
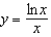 has a horizontal tangent.
has a horizontal tangent.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
64
Let . Find the value of .
A)
B)
C)
D)1
E)
F)
G)
H)
A)
B)
C)
D)1
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
65
Let . Find the value of .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
66
Find 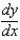 .(a)
.(a) 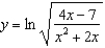 (b)
(b) 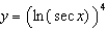 (c)
(c) 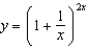
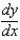 .(a)
.(a) 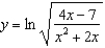 (b)
(b) 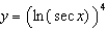 (c)
(c) 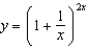

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
67
Simplify the expression 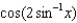 .
.
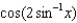 .
.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
68
Find the critical numbers for 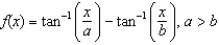 and identify each as a relative maximum, relative minimum, or neither.
and identify each as a relative maximum, relative minimum, or neither.
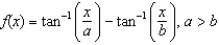 and identify each as a relative maximum, relative minimum, or neither.
and identify each as a relative maximum, relative minimum, or neither.
Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
69
Let .(a) Show that is constant on .(b) Determine the value of the constant(s).

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
70
Find the domain of the function .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
71
Let . Find the value of .
A)0
B)0.1
C)0.2
D)0.3
E)0.4
F)0.5
G)0.6
H)0.8
A)0
B)0.1
C)0.2
D)0.3
E)0.4
F)0.5
G)0.6
H)0.8

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
72
Find the derivatives of the following functions:
(a)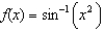 (b)
(b) 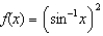 (c)
(c) 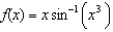 (d)
(d) 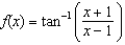 (e)
(e) 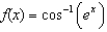
(a)
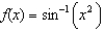 (b)
(b) 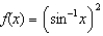 (c)
(c) 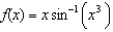 (d)
(d) 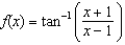 (e)
(e) 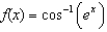

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
73
If find the value of at the point (3, 4).
A)
B)
C)
D)
E)0
F)1
G)
H)
A)
B)
C)
D)
E)0
F)1
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
74
Let . Find the value of .
A)
B).2
C)
D)1
E)
F)
G).0
H)
A)
B).2
C)
D)1
E)
F)
G).0
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
75
Simplify the express: .
A)1
B)
C)
D)
E)
F)
G)
H)
A)1
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
76
Find the exact value of .
A)
B)
C)0
D)
E)
F)
G)
H)
A)
B)
C)0
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
77
Find 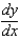 .(a)
.(a) 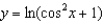 (b)
(b) 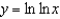
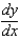 .(a)
.(a) 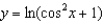 (b)
(b) 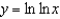

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
78
Find the exact value of .
A)1
B)
C)
D)
E)0
F)
G)
H)
A)1
B)
C)
D)
E)0
F)
G)
H)

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
79
Differentiate the following functions:
(a)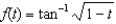 (b)
(b) 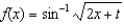 (c)
(c) 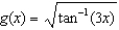
(a)
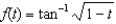 (b)
(b) 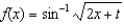 (c)
(c) 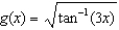

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck
80
Find 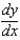 implicitly:
implicitly:
(a)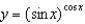 (b)
(b) 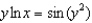
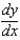 implicitly:
implicitly:(a)
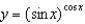 (b)
(b) 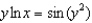

Unlock Deck
Unlock for access to all 248 flashcards in this deck.
Unlock Deck
k this deck


