Deck 13: Vector Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/240
Play
Full screen (f)
Deck 13: Vector Calculus
1
Let 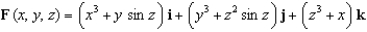 and let S be the boundary surface of the solid E bounded by
and let S be the boundary surface of the solid E bounded by 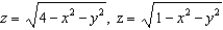 , and
, and 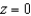 . Evaluate the surface integral
. Evaluate the surface integral 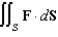 .
.
A)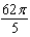 e.
e. 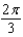 b.
b. 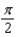 f.
f. 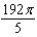 c.
c. 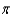 g.
g. 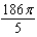 d.
d. 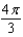 h.
h. 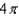
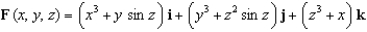 and let S be the boundary surface of the solid E bounded by
and let S be the boundary surface of the solid E bounded by 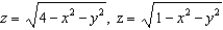 , and
, and 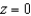 . Evaluate the surface integral
. Evaluate the surface integral 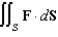 .
.A)
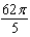 e.
e. 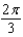 b.
b. 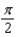 f.
f. 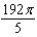 c.
c. 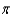 g.
g. 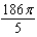 d.
d. 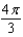 h.
h. 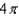
G
2
Find the flux of 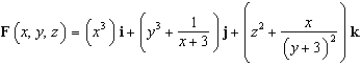 across the surface of the solid bounded by
across the surface of the solid bounded by 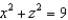 , and the planes
, and the planes 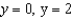 .
.
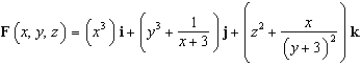 across the surface of the solid bounded by
across the surface of the solid bounded by 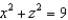 , and the planes
, and the planes 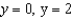 .
.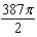
3
Let 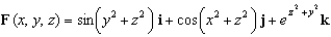 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 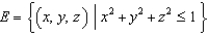 . Evaluate the surface integral
. Evaluate the surface integral 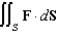 .
.
A)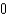 e.
e. 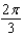 b.
b. 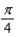 f.
f. 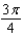 c.
c. 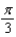 g.
g. 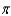 d.
d. 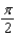 h.
h. 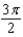
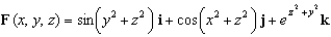 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 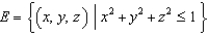 . Evaluate the surface integral
. Evaluate the surface integral 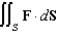 .
.A)
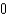 e.
e. 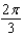 b.
b. 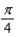 f.
f. 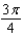 c.
c. 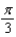 g.
g. 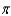 d.
d. 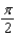 h.
h. 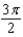
A
4
Let 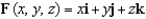 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 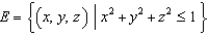 . Evaluate the surface integral
. Evaluate the surface integral 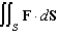 .
.
A)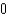 e.
e. 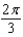 b.
b. 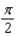 f.
f. 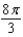 c.
c. 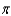 g.
g. 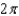 d.
d. 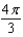 h.
h. 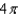
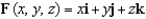 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 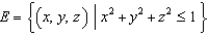 . Evaluate the surface integral
. Evaluate the surface integral 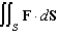 .
.A)
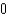 e.
e. 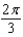 b.
b. 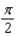 f.
f. 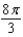 c.
c. 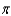 g.
g. 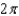 d.
d. 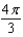 h.
h. 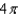

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
5
Let 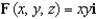 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 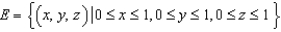 . Evaluate the surface integral
. Evaluate the surface integral 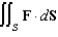 .
.
A)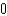 e.
e. 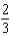 b.
b. 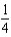 f.
f. 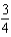 c.
c. 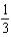 g.
g. 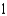 d.
d. 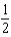 h.
h. 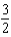
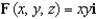 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 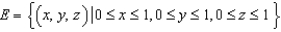 . Evaluate the surface integral
. Evaluate the surface integral 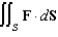 .
.A)
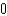 e.
e. 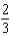 b.
b. 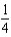 f.
f. 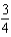 c.
c. 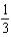 g.
g. 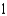 d.
d. 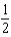 h.
h. 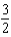

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
6
Let 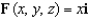 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 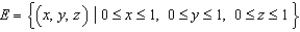 . Evaluate the surface integral
. Evaluate the surface integral 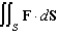 .
.
A)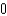 e.
e. 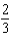 b.
b. 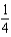 f.
f. 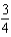 c.
c. 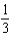 g.
g. 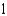 d.
d. 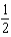 h.
h. 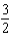
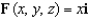 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 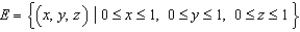 . Evaluate the surface integral
. Evaluate the surface integral 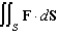 .
.A)
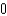 e.
e. 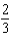 b.
b. 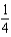 f.
f. 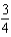 c.
c. 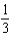 g.
g. 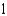 d.
d. 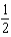 h.
h. 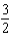

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
7
Let 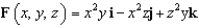 and let S be the surface of the rectangular box bounded by the planes
and let S be the surface of the rectangular box bounded by the planes  , and
, and 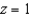 . Evaluate the surface integral
. Evaluate the surface integral 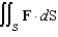 .
.
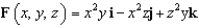 and let S be the surface of the rectangular box bounded by the planes
and let S be the surface of the rectangular box bounded by the planes  , and
, and 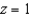 . Evaluate the surface integral
. Evaluate the surface integral 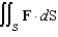 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
8
Let 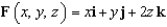 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 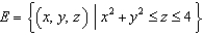 . Evaluate the surface integral
. Evaluate the surface integral 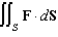 .
.
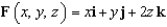 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 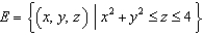 . Evaluate the surface integral
. Evaluate the surface integral 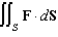 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
9
Let 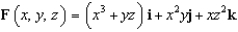 and let S be the surface of the solid bounded by the spheres
and let S be the surface of the solid bounded by the spheres 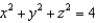 and
and 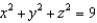 . Evaluate the surface integral
. Evaluate the surface integral 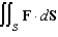 .
.
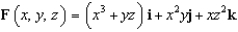 and let S be the surface of the solid bounded by the spheres
and let S be the surface of the solid bounded by the spheres 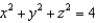 and
and 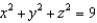 . Evaluate the surface integral
. Evaluate the surface integral 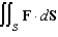 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate 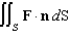 , where S is the cube bounded by the planes
, where S is the cube bounded by the planes 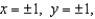 and
and 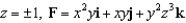 , and n is the outward normal.
, and n is the outward normal.
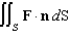 , where S is the cube bounded by the planes
, where S is the cube bounded by the planes 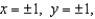 and
and 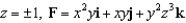 , and n is the outward normal.
, and n is the outward normal.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
11
Let 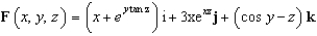 and let S be the surface with equation
and let S be the surface with equation 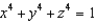 . Evaluate the surface integral
. Evaluate the surface integral 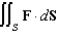 .
.
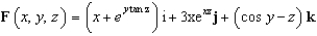 and let S be the surface with equation
and let S be the surface with equation 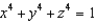 . Evaluate the surface integral
. Evaluate the surface integral 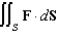 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
12
Let 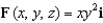 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 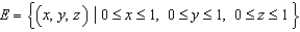 . Evaluate the surface integral
. Evaluate the surface integral 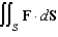 .
.
A)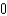 e.
e. 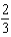 b.
b. 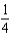 f.
f. 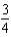 c.
c. 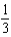 g.
g. 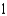 d.
d. 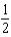 h.
h. 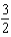
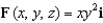 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 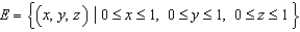 . Evaluate the surface integral
. Evaluate the surface integral 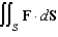 .
.A)
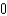 e.
e. 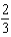 b.
b. 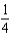 f.
f. 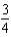 c.
c. 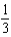 g.
g. 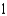 d.
d. 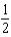 h.
h. 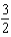

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
13
Use the Divergence Theorem to evaluate 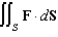 where
where 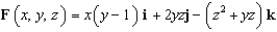 and S is the surface of the cylinder
and S is the surface of the cylinder 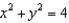 , bounded by the planes
, bounded by the planes 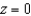 and
and 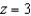 .
.
A)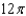 e.
e. 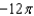 b.
b. 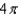 f.
f. 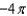 c.
c. 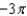 g.
g. 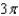 d.
d. 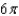 h.
h. 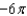
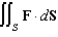 where
where 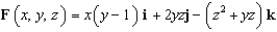 and S is the surface of the cylinder
and S is the surface of the cylinder 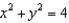 , bounded by the planes
, bounded by the planes 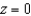 and
and 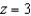 .
.A)
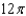 e.
e. 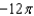 b.
b. 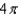 f.
f. 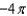 c.
c. 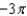 g.
g. 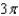 d.
d. 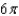 h.
h. 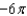

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
14
Find the flux of 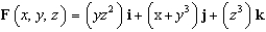 across the surface of the solid bounded by the paraboloid
across the surface of the solid bounded by the paraboloid 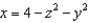 and the
and the 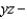 plane.
plane.
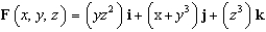 across the surface of the solid bounded by the paraboloid
across the surface of the solid bounded by the paraboloid 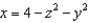 and the
and the 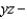 plane.
plane.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
15
Let 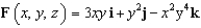 and let S be the surface of the tetrahedron with vertices
and let S be the surface of the tetrahedron with vertices 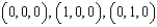 , and
, and 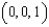 . Evaluate the surface integral
. Evaluate the surface integral 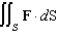 .
.
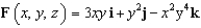 and let S be the surface of the tetrahedron with vertices
and let S be the surface of the tetrahedron with vertices 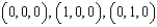 , and
, and 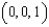 . Evaluate the surface integral
. Evaluate the surface integral 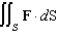 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
16
Let 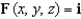 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 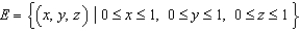 . Evaluate the surface integral
. Evaluate the surface integral 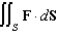 .
.
A)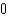 e.
e. 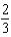 b.
b. 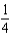 f.
f. 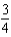 c.
c. 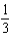 g.
g. 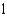 d.
d. 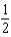 h.
h. 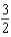
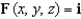 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 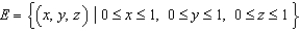 . Evaluate the surface integral
. Evaluate the surface integral 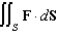 .
.A)
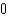 e.
e. 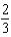 b.
b. 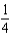 f.
f. 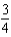 c.
c. 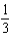 g.
g. 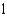 d.
d. 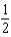 h.
h. 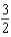

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
17
Use the Divergence Theorem to evaluate 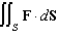 where
where 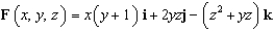 and S is the sphere
and S is the sphere 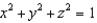 .
.
A)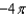 e.
e. 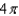 b.
b. 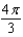 f.
f. 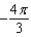 c.
c. 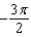 g.
g. 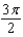 d.
d. 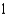 h.
h. 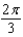
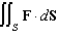 where
where 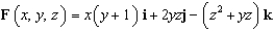 and S is the sphere
and S is the sphere 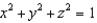 .
.A)
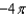 e.
e. 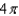 b.
b. 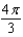 f.
f. 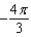 c.
c. 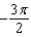 g.
g. 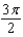 d.
d. 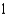 h.
h. 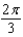

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
18
Let 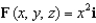 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 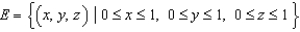 . Evaluate the surface integral
. Evaluate the surface integral 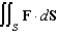 .
.
A)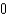 e.
e. 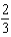 b.
b. 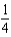 f.
f. 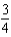 c.
c. 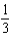 g.
g. 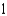 d.
d. 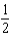 h.
h. 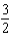
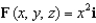 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 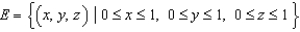 . Evaluate the surface integral
. Evaluate the surface integral 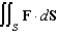 .
.A)
 e.
e. 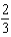 b.
b. 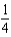 f.
f. 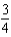 c.
c. 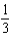 g.
g. 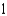 d.
d. 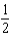 h.
h. 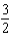

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
19
Let 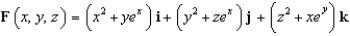 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 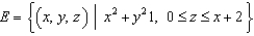 . Evaluate the surface integral
. Evaluate the surface integral 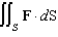 .
.
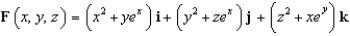 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 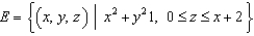 . Evaluate the surface integral
. Evaluate the surface integral 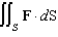 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the flux integral 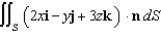 over the boundary of the ball
over the boundary of the ball 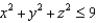 .
.
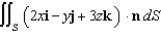 over the boundary of the ball
over the boundary of the ball 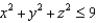 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate 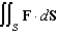 , where S is the boundary surface of the solid sphere
, where S is the boundary surface of the solid sphere 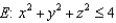 and
and 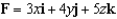
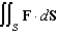 , where S is the boundary surface of the solid sphere
, where S is the boundary surface of the solid sphere 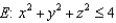 and
and 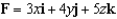

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate 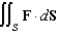 , where S is the boundary surface of the region outside the sphere
, where S is the boundary surface of the region outside the sphere 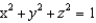 and inside the ball
and inside the ball 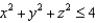 and
and 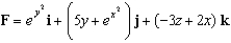 .
.
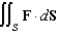 , where S is the boundary surface of the region outside the sphere
, where S is the boundary surface of the region outside the sphere 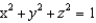 and inside the ball
and inside the ball 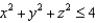 and
and 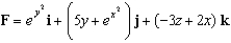 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
23
Let 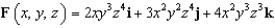 . Evaluate the line integral
. Evaluate the line integral 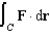 along the elliptical path
along the elliptical path 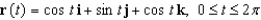 .
.
A)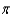 e.
e. 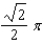 b.
b. 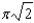 f.
f. 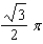 c.
c. 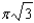 g.
g. 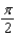 d.
d. 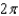 h.
h. 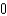
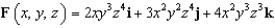 . Evaluate the line integral
. Evaluate the line integral 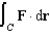 along the elliptical path
along the elliptical path 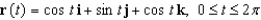 .
.A)
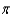 e.
e. 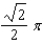 b.
b. 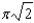 f.
f. 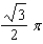 c.
c. 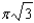 g.
g. 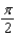 d.
d. 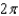 h.
h. 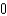

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
24
Let S be the outwardly-oriented surface of a solid region E where the volume of E is 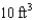 . If
. If 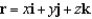 and
and 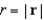 , evaluate the surface integral
, evaluate the surface integral 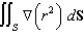 .
.
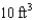 . If
. If 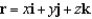 and
and 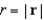 , evaluate the surface integral
, evaluate the surface integral 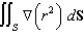 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
25
Use Stokes' Theorem to evaluate 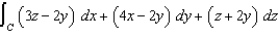 where C is the circle
where C is the circle 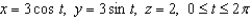 .
.
A)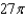 e.
e. 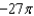 b.
b. 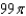 f.
f. 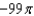 c.
c. 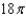 g.
g. 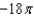 d.
d. 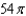 h.
h. 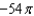
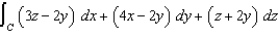 where C is the circle
where C is the circle 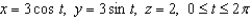 .
.A)
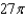 e.
e. 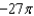 b.
b. 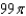 f.
f. 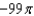 c.
c. 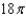 g.
g. 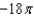 d.
d. 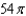 h.
h. 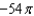

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate 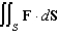 , where
, where 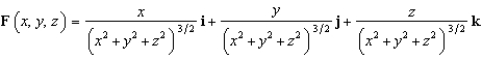 and S is the sphere
and S is the sphere 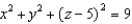 .
.
 , where
, where  and S is the sphere
and S is the sphere  .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
27
Use Stokes' Theorem to evaluate  where
where 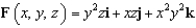 and S is the part of the paraboloid
and S is the part of the paraboloid 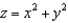 that lies inside the cylinder
that lies inside the cylinder 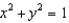 , oriented upward.
, oriented upward.
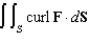 where
where 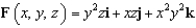 and S is the part of the paraboloid
and S is the part of the paraboloid 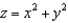 that lies inside the cylinder
that lies inside the cylinder 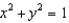 , oriented upward.
, oriented upward.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
28
Let 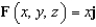 . Evaluate the line integral
. Evaluate the line integral 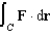 along the elliptical path
along the elliptical path 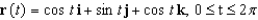 .
.
A)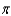 e.
e. 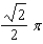 b.
b. 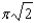 f.
f. 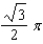 c.
c. 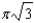 g.
g. 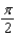 d.
d. 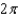 h.
h. 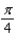
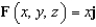 . Evaluate the line integral
. Evaluate the line integral 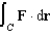 along the elliptical path
along the elliptical path 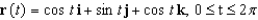 .
.A)
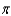 e.
e. 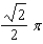 b.
b. 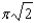 f.
f. 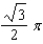 c.
c. 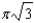 g.
g. 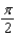 d.
d. 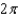 h.
h. 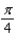

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
29
Let 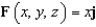 . Evaluate the line integral
. Evaluate the line integral 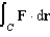 along the rectangular path from
along the rectangular path from 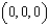 to
to 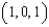 to
to 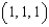 to
to 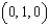 to
to 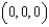 .
.
A)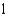 e.
e. 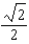 b.
b. 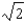 f.
f. 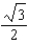 c.
c. 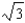 g.
g. 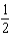 d.
d. 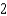 h.
h. 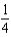
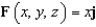 . Evaluate the line integral
. Evaluate the line integral 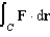 along the rectangular path from
along the rectangular path from 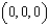 to
to 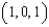 to
to 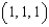 to
to 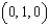 to
to 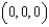 .
.A)
 e.
e. 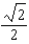 b.
b. 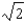 f.
f. 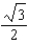 c.
c. 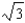 g.
g. 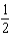 d.
d. 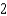 h.
h. 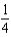

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
30
Let 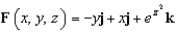 . Evaluate
. Evaluate 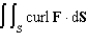 over the surface S given by
over the surface S given by 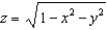 , with downward orientation.
, with downward orientation.
A)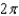 e.
e. 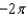 b.
b. 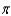 f.
f. 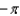 c.
c. 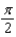 g.
g. 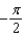 d.
d. 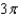 h.
h. 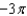
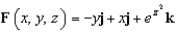 . Evaluate
. Evaluate 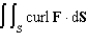 over the surface S given by
over the surface S given by 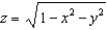 , with downward orientation.
, with downward orientation.A)
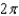 e.
e. 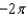 b.
b. 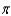 f.
f. 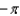 c.
c. 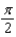 g.
g. 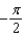 d.
d. 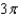 h.
h. 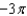

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
31
Find the flux of 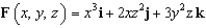 across the surface of the solid bounded by the paraboloid
across the surface of the solid bounded by the paraboloid 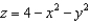 and the
and the 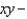 plane.
plane.
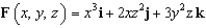 across the surface of the solid bounded by the paraboloid
across the surface of the solid bounded by the paraboloid 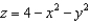 and the
and the 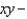 plane.
plane.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate 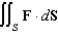 , where
, where 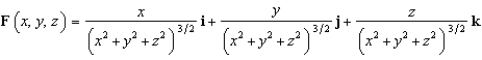 and S is the sphere
and S is the sphere 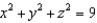 .
.
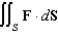 , where
, where 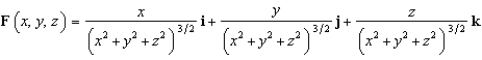 and S is the sphere
and S is the sphere 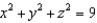 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
33
Find the flux of 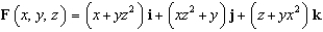 across the surface of the solid bounded by the paraboloid
across the surface of the solid bounded by the paraboloid 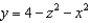 and the
and the 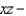 plane.
plane.
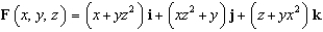 across the surface of the solid bounded by the paraboloid
across the surface of the solid bounded by the paraboloid 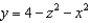 and the
and the 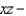 plane.
plane.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
34
Let 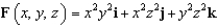 . Let C be the rectangular path from
. Let C be the rectangular path from 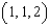 to
to 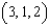 to
to 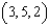 to
to 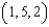 to
to 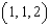 . Use Stokes' Theorem to evaluate the line integral
. Use Stokes' Theorem to evaluate the line integral 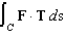 , where T is the unit tangent vector to C.
, where T is the unit tangent vector to C.
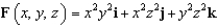 . Let C be the rectangular path from
. Let C be the rectangular path from 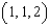 to
to 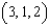 to
to 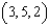 to
to 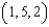 to
to 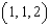 . Use Stokes' Theorem to evaluate the line integral
. Use Stokes' Theorem to evaluate the line integral 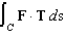 , where T is the unit tangent vector to C.
, where T is the unit tangent vector to C.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
35
Find the flux of 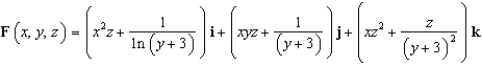 across the surface of the solid
across the surface of the solid 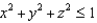 .
.
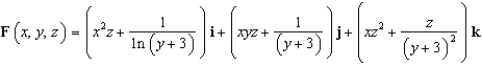 across the surface of the solid
across the surface of the solid 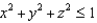 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate 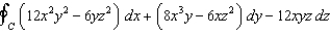 , where the path C is the curve of intersection of the paraboloid
, where the path C is the curve of intersection of the paraboloid 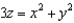 with the plane
with the plane 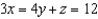 .
.
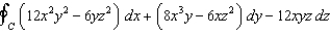 , where the path C is the curve of intersection of the paraboloid
, where the path C is the curve of intersection of the paraboloid 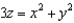 with the plane
with the plane 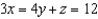 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
37
Let 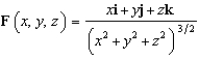 . Evaluate the line integral
. Evaluate the line integral 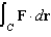 , where C is the curve of intersection of the paraboloid
, where C is the curve of intersection of the paraboloid 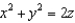 and the cylinder
and the cylinder 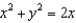 .
.
A)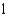 e.
e. 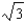 b.
b. 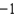 f.
f. 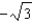 c.
c. 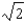 g.
g. 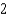 d.
d. 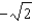 h.
h. 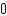
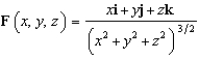 . Evaluate the line integral
. Evaluate the line integral 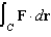 , where C is the curve of intersection of the paraboloid
, where C is the curve of intersection of the paraboloid 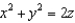 and the cylinder
and the cylinder 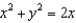 .
.A)
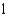 e.
e. 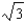 b.
b. 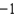 f.
f. 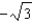 c.
c. 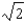 g.
g. 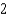 d.
d. 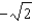 h.
h. 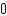

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
38
Use Stokes' Theorem to evaluate 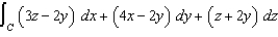 where C is the circle
where C is the circle 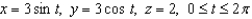 .
.
A)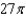 e.
e. 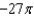 b.
b. 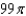 f.
f. 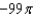 c.
c. 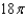 g.
g. 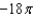 d.
d. 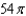 h.
h. 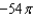
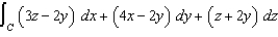 where C is the circle
where C is the circle 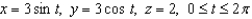 .
.A)
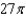 e.
e. 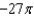 b.
b. 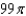 f.
f. 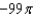 c.
c. 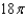 g.
g. 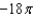 d.
d. 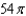 h.
h. 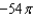

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
39
Use Stokes' Theorem to evaluate 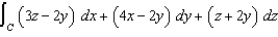 where C is the triangle with vertices
where C is the triangle with vertices 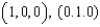 , and
, and 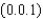 , oriented counter clockwise as viewed from above.
, oriented counter clockwise as viewed from above.
A)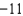 e.
e. 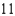 b.
b. 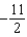 f.
f. 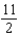 c.
c. 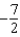 g.
g. 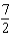 d.
d. 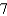 h.
h. 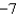
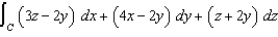 where C is the triangle with vertices
where C is the triangle with vertices 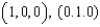 , and
, and 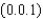 , oriented counter clockwise as viewed from above.
, oriented counter clockwise as viewed from above.A)
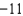 e.
e. 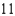 b.
b. 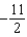 f.
f. 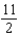 c.
c. 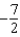 g.
g. 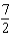 d.
d. 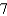 h.
h. 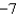

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
40
Let 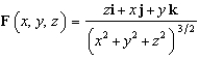 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 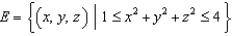 . Evaluate the surface integral
. Evaluate the surface integral 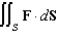 .
.
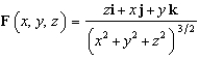 and let S be the boundary surface of the solid
and let S be the boundary surface of the solid 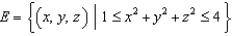 . Evaluate the surface integral
. Evaluate the surface integral 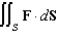 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
41
A surface has the shape of the cone 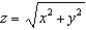 between
between 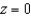 and
and 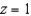 with the density function
with the density function 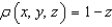 . Find the mass of the surface.
. Find the mass of the surface.
A)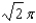
B)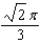
C)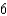
D)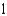
E)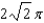
F)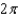
G)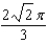
H)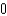
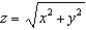 between
between 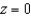 and
and 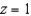 with the density function
with the density function 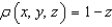 . Find the mass of the surface.
. Find the mass of the surface.A)
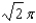
B)
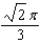
C)
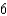
D)
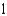
E)
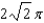
F)
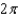
G)
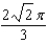
H)
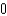

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the surfaces 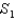 :
: 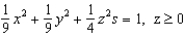 , and
, and 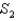 :
: 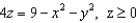 , and let F be a vector field with continuous partial derivatives everywhere. Why do we know that
, and let F be a vector field with continuous partial derivatives everywhere. Why do we know that 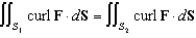 ?
?
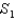 :
: 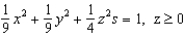 , and
, and  :
:  , and let F be a vector field with continuous partial derivatives everywhere. Why do we know that
, and let F be a vector field with continuous partial derivatives everywhere. Why do we know that 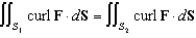 ?
?
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
43
Use Stokes' Theorem to evaluate 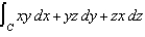 , where C is the triangle with vertices
, where C is the triangle with vertices 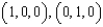 , and
, and 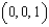 , oriented counterclockwise as viewed from above.
, oriented counterclockwise as viewed from above.
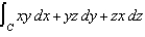 , where C is the triangle with vertices
, where C is the triangle with vertices 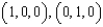 , and
, and 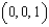 , oriented counterclockwise as viewed from above.
, oriented counterclockwise as viewed from above.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
44
Use Stokes' Theorem to evaluate 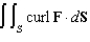 where
where 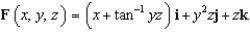 and S is the part of the hemisphere
and S is the part of the hemisphere 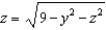 that lies inside the cylinder
that lies inside the cylinder 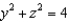 , oriented in the direction of the positive x-axis.
, oriented in the direction of the positive x-axis.
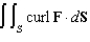 where
where 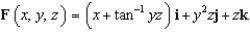 and S is the part of the hemisphere
and S is the part of the hemisphere 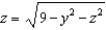 that lies inside the cylinder
that lies inside the cylinder 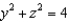 , oriented in the direction of the positive x-axis.
, oriented in the direction of the positive x-axis.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the surface integral 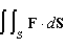 , where
, where 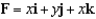 and S is the part of the plane
and S is the part of the plane 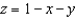 in the first octant with downward orientation.
in the first octant with downward orientation.
A)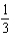
B)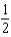
C)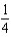
D)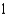
E)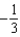
F)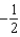
G)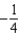
H)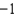
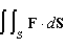 , where
, where 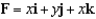 and S is the part of the plane
and S is the part of the plane 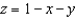 in the first octant with downward orientation.
in the first octant with downward orientation.A)
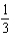
B)
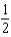
C)
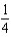
D)
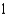
E)
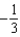
F)
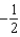
G)
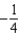
H)
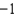

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate 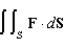 , where
, where 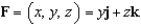 and S is the cube bounded by
and S is the cube bounded by 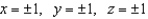 .
.
A)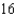
B)
C)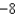
D)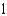
E)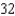
F)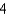
G)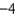
H)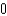
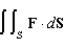 , where
, where 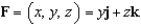 and S is the cube bounded by
and S is the cube bounded by 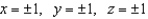 .
.A)
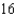
B)

C)
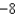
D)
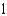
E)
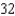
F)
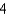
G)
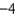
H)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the surface integral 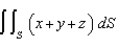 , where S is that part of the plane
, where S is that part of the plane 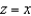 that lies above the square with vertices
that lies above the square with vertices 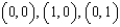 , and
, and 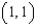 .
.
A)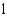
B)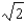
C)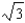
D)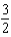
E)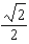
F)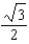
G)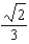
H)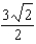
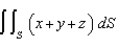 , where S is that part of the plane
, where S is that part of the plane 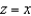 that lies above the square with vertices
that lies above the square with vertices 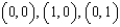 , and
, and 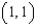 .
.A)
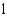
B)
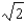
C)
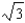
D)
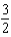
E)
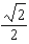
F)
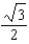
G)
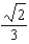
H)
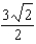

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
48
Verify that Stokes' Theorem is true for the vector field 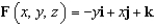 and the cone
and the cone 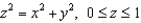 , oriented upward.
, oriented upward.
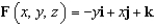 and the cone
and the cone 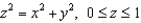 , oriented upward.
, oriented upward.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
49
Let 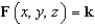 . Evaluate the surface integral
. Evaluate the surface integral 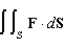 , where S is that part of the plane
, where S is that part of the plane 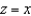 that lies above the square with vertices
that lies above the square with vertices 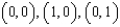 , and
, and 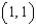 and has upward orientation.
and has upward orientation.
A)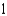
B)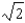
C)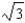
D)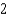
E)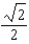
F)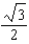
G)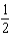
H)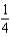
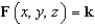 . Evaluate the surface integral
. Evaluate the surface integral 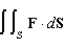 , where S is that part of the plane
, where S is that part of the plane 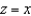 that lies above the square with vertices
that lies above the square with vertices 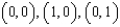 , and
, and 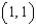 and has upward orientation.
and has upward orientation.A)
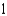
B)
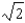
C)
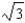
D)
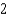
E)
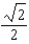
F)
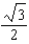
G)
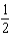
H)
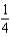

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
50
Evaluate 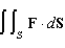 where
where 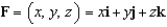 and S is the part of the surface
and S is the part of the surface 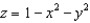 that lies above the
that lies above the 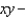 plane and has upward orientation.
plane and has upward orientation.
A)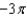
B)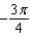
C)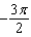
D)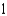
E)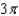
F)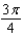
G)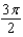
H)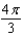
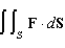 where
where 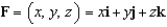 and S is the part of the surface
and S is the part of the surface 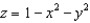 that lies above the
that lies above the 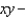 plane and has upward orientation.
plane and has upward orientation.A)
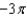
B)
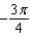
C)
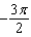
D)
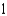
E)
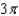
F)
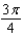
G)
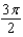
H)
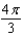

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
51
Let S be the parametric surface 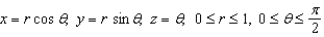 . Use Stokes' Theorem to evaluate
. Use Stokes' Theorem to evaluate 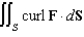 , where
, where 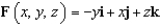 .
.
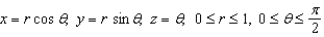 . Use Stokes' Theorem to evaluate
. Use Stokes' Theorem to evaluate 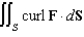 , where
, where 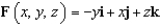 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
52
Use Stokes' Theorem to evaluate 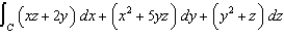 , where C is the curve of intersection of the paraboloid
, where C is the curve of intersection of the paraboloid 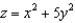 and the cylinder
and the cylinder 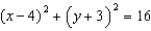 , oriented counterclockwise as viewed from above.
, oriented counterclockwise as viewed from above.
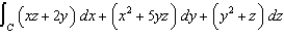 , where C is the curve of intersection of the paraboloid
, where C is the curve of intersection of the paraboloid 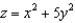 and the cylinder
and the cylinder 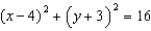 , oriented counterclockwise as viewed from above.
, oriented counterclockwise as viewed from above.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
53
An upper hemisphere is given by 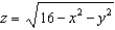 with the density function
with the density function 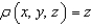 . Find the mass of the sphere.
. Find the mass of the sphere.
A)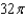
B)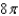
C)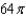
D)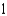
E)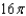
F)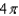
G)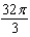
H)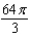
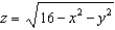 with the density function
with the density function 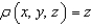 . Find the mass of the sphere.
. Find the mass of the sphere.A)
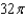
B)
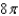
C)
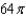
D)
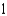
E)
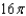
F)
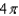
G)
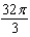
H)
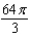

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the surface integral 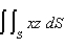 , where S is the triangle with vertices
, where S is the triangle with vertices 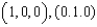 , and
, and 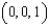
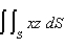 , where S is the triangle with vertices
, where S is the triangle with vertices 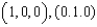 , and
, and 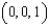

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
55
Let 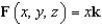 . Evaluate the surface integral
. Evaluate the surface integral 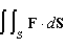 , where S is that part of the plane
, where S is that part of the plane 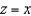 that lies above the square with vertices
that lies above the square with vertices 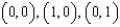 , and
, and 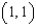 and has upward orientation.
and has upward orientation.
A)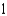
B)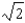
C)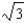
D)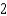
E)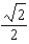
F)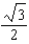
G)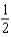
H)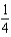
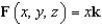 . Evaluate the surface integral
. Evaluate the surface integral 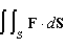 , where S is that part of the plane
, where S is that part of the plane 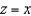 that lies above the square with vertices
that lies above the square with vertices 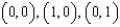 , and
, and 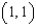 and has upward orientation.
and has upward orientation.A)
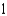
B)
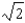
C)
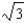
D)
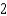
E)
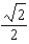
F)
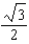
G)
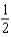
H)
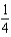

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate the surface integral 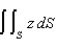 , where S is that part of the cylinder
, where S is that part of the cylinder 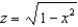 that lies above the square with vertices
that lies above the square with vertices 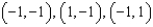 , and
, and 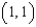 .
.
A)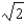
B)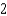
C)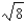
D)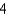
E)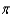
F)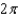
G)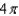
H)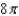
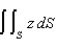 , where S is that part of the cylinder
, where S is that part of the cylinder 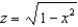 that lies above the square with vertices
that lies above the square with vertices 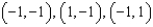 , and
, and 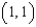 .
.A)
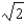
B)
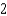
C)
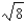
D)
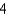
E)
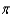
F)
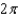
G)
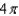
H)
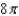

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
57
Use Stokes' Theorem to evaluate 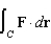 where
where 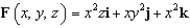 and C is the curve of intersection of the plane
and C is the curve of intersection of the plane 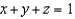 and the cylinder
and the cylinder 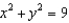 .
.
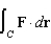 where
where 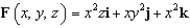 and C is the curve of intersection of the plane
and C is the curve of intersection of the plane 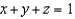 and the cylinder
and the cylinder 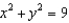 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate 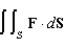 , where
, where 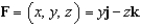 and S is the cube bounded by
and S is the cube bounded by 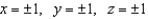 .
.
A)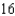
B)
C)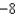
D)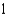
E)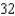
F)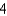
G)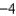
H)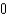
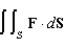 , where
, where 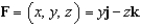 and S is the cube bounded by
and S is the cube bounded by 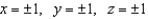 .
.A)
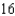
B)

C)
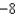
D)
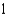
E)
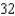
F)
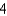
G)
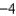
H)
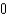

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the surface integral 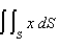 , where S is that part of the plane
, where S is that part of the plane 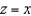 that lies above the square with vertices
that lies above the square with vertices 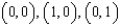 , and
, and 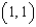 .
.
A)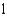
B)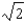
C)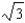
D)2
E)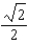
F)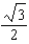
G)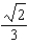
H)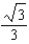
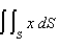 , where S is that part of the plane
, where S is that part of the plane 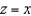 that lies above the square with vertices
that lies above the square with vertices 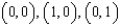 , and
, and 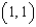 .
.A)
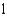
B)
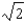
C)
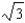
D)2
E)
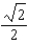
F)
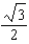
G)
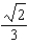
H)
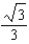

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
60
Use Stokes' Theorem to evaluate 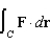 where
where 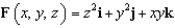 and C is the triangle with vertices
and C is the triangle with vertices 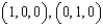 , and
, and 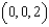
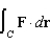 where
where 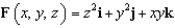 and C is the triangle with vertices
and C is the triangle with vertices 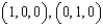 , and
, and 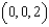

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
61
A fluid has density 1500 and velocity field 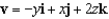 . Find the rate of flow outward through the sphere
. Find the rate of flow outward through the sphere 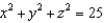 .
.
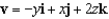 . Find the rate of flow outward through the sphere
. Find the rate of flow outward through the sphere 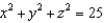 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate 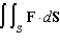 , where
, where 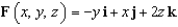 and S is the upper half of the sphere
and S is the upper half of the sphere 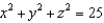 , with upward orientation.
, with upward orientation.
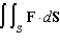 , where
, where 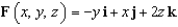 and S is the upper half of the sphere
and S is the upper half of the sphere 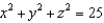 , with upward orientation.
, with upward orientation.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the surface integral 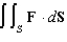 for the vector field
for the vector field 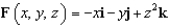 where S is part of the cone
where S is part of the cone 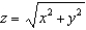 between the planes z = 1 and z = 2 with upward orientation.
between the planes z = 1 and z = 2 with upward orientation.
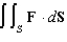 for the vector field
for the vector field 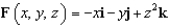 where S is part of the cone
where S is part of the cone 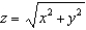 between the planes z = 1 and z = 2 with upward orientation.
between the planes z = 1 and z = 2 with upward orientation.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the flux of the vector field 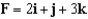 through the plane region with the given orientation as shown below.
through the plane region with the given orientation as shown below. 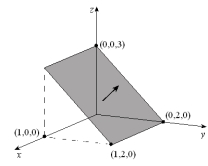
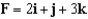 through the plane region with the given orientation as shown below.
through the plane region with the given orientation as shown below. 

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate 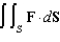 where
where 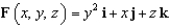 and S is the part of the surface
and S is the part of the surface 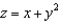 that lies above the rectangle
that lies above the rectangle 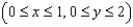 and has upward orientation.
and has upward orientation.
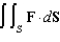 where
where 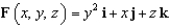 and S is the part of the surface
and S is the part of the surface 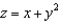 that lies above the rectangle
that lies above the rectangle 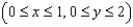 and has upward orientation.
and has upward orientation.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the surface integral 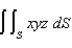 , where S is the part of the sphere
, where S is the part of the sphere 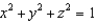 that lies above the cone
that lies above the cone 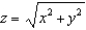 .
.
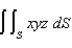 , where S is the part of the sphere
, where S is the part of the sphere 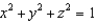 that lies above the cone
that lies above the cone 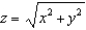 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the surface integral 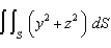 , where S is the part of the paraboloid
, where S is the part of the paraboloid  that lies in front of the plane
that lies in front of the plane 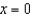 .
.
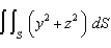 , where S is the part of the paraboloid
, where S is the part of the paraboloid  that lies in front of the plane
that lies in front of the plane 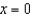 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
68
Compute the surface integral 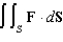 if
if 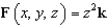 and S is the piece of the sphere
and S is the piece of the sphere 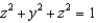 in the second octant
in the second octant 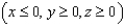 .
.
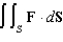 if
if 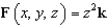 and S is the piece of the sphere
and S is the piece of the sphere 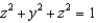 in the second octant
in the second octant 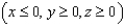 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the top half of the ellipsoid 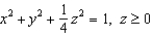 parametrized by
parametrized by 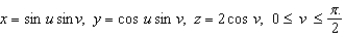 . Find a normal vector N at the point determined by
. Find a normal vector N at the point determined by 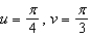 , and determine if it is upward and/or outward.
, and determine if it is upward and/or outward.
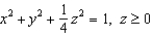 parametrized by
parametrized by 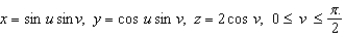 . Find a normal vector N at the point determined by
. Find a normal vector N at the point determined by 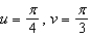 , and determine if it is upward and/or outward.
, and determine if it is upward and/or outward.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the flux of the vector field 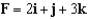 through the plane region with the given orientation as shown below.
through the plane region with the given orientation as shown below. 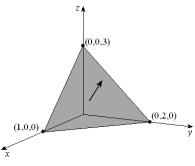
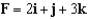 through the plane region with the given orientation as shown below.
through the plane region with the given orientation as shown below. 

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate the surface integral 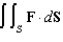 for the vector field
for the vector field 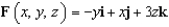 , where S is the hemisphere
, where S is the hemisphere 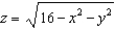 with upward orientation.
with upward orientation.
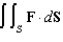 for the vector field
for the vector field 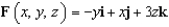 , where S is the hemisphere
, where S is the hemisphere 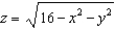 with upward orientation.
with upward orientation.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
72
Find the flux of the vector field 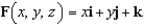 across the paraboloid given by
across the paraboloid given by 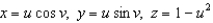 with
with 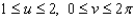 and upward orientation:
and upward orientation:
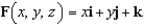 across the paraboloid given by
across the paraboloid given by 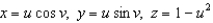 with
with 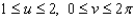 and upward orientation:
and upward orientation:
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
73
Find the z-coordinate of the centroid of the upper hemisphere with uniform density whose equation is given by 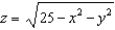 .
.
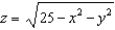 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
74
Find the mass of the sphere 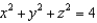 whose density at each point is proportional to its distance to the
whose density at each point is proportional to its distance to the 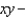 plane.
plane.
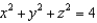 whose density at each point is proportional to its distance to the
whose density at each point is proportional to its distance to the 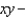 plane.
plane.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
75
Evaluate 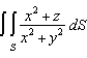 , where S is the part of the surface
, where S is the part of the surface 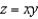 that lies between the cylinders
that lies between the cylinders 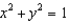 and
and 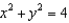 .
.
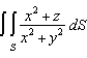 , where S is the part of the surface
, where S is the part of the surface 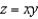 that lies between the cylinders
that lies between the cylinders 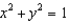 and
and 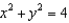 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate 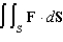 , where
, where 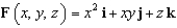 and S is the part of the surface
and S is the part of the surface 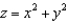 below the plane
below the plane 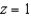 , with upward orientation.
, with upward orientation.
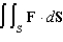 , where
, where 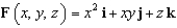 and S is the part of the surface
and S is the part of the surface 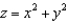 below the plane
below the plane 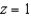 , with upward orientation.
, with upward orientation.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate the surface integral 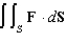 for the vector field
for the vector field 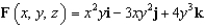 where S is the part of the elliptic paraboloid
where S is the part of the elliptic paraboloid 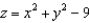 that lies below the square
that lies below the square 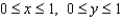 and has downward orientation.
and has downward orientation.
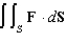 for the vector field
for the vector field 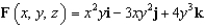 where S is the part of the elliptic paraboloid
where S is the part of the elliptic paraboloid 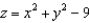 that lies below the square
that lies below the square 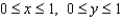 and has downward orientation.
and has downward orientation.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
78
Let 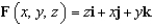 . Find the curl of F.
. Find the curl of F.
A)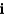
B)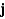
C)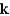
D)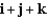
E)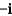
F)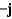
G)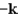
H)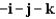
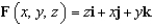 . Find the curl of F.
. Find the curl of F.A)
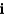
B)
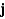
C)
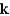
D)
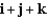
E)
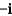
F)
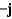
G)
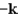
H)
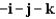

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
79
Find the mass of a thin funnel in the shape of a cone 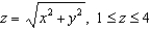 , is its density
, is its density
function is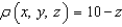 .
.
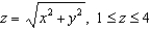 , is its density
, is its densityfunction is
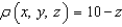 .
.
Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
80
Let 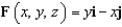 . Find the curl of F.
. Find the curl of F.
A)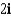
B)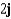
C)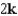
D)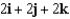
E)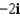
F)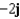
G)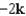
H)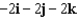
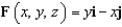 . Find the curl of F.
. Find the curl of F.A)
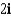
B)
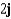
C)
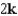
D)
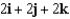
E)
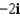
F)
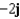
G)
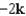
H)
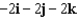

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck


