Deck 5: Probability, Normal Distributions, and Z Scores
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/80
Play
Full screen (f)
Deck 5: Probability, Normal Distributions, and Z Scores
1
A gambler rolls a 3 with one roll of a single fair die.Given that the die was six-sided,what was the probability of rolling a 3 with one roll?
A)1/6
B)3/6
C)1/9
D)3/9
A)1/6
B)3/6
C)1/9
D)3/9
1/6
2
A researcher determines the probability that a research study will reveal something new is p = .80.What is the probability that the study will reveal something new or not reveal something new?
A).80
B).64
C)1.00
D).16
A).80
B).64
C)1.00
D).16
1.00
3
Two outcomes are said to be mutually exclusive when
A)the probability of the two outcomes occurring together is equal to zero (p = 0)
B)the probability of the occurrence of one outcome has no effect on the probability of the occurrence of the second outcome
C)the probability of the two outcomes occurring together is greater than zero (p > 0)
D)the probability of the two outcomes occurring together sums to one
A)the probability of the two outcomes occurring together is equal to zero (p = 0)
B)the probability of the occurrence of one outcome has no effect on the probability of the occurrence of the second outcome
C)the probability of the two outcomes occurring together is greater than zero (p > 0)
D)the probability of the two outcomes occurring together sums to one
the probability of the two outcomes occurring together is equal to zero (p = 0)
4
A researcher determines that the probability of winning a new game is p = .32.Assuming winning and losing are mutually exclusive events,what is the probability of winning and losing the new game?
A).22
B).68
C)1.00
D)This outcome is not possible.
A).22
B).68
C)1.00
D)This outcome is not possible.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
5
The proportion or fraction of times an outcome is likely to occur is referred to as
A)probability
B)a random event
C)sample space
D)luck
A)probability
B)a random event
C)sample space
D)luck

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
6
A researcher has participants choose between three advertisements.She finds that 54 prefer Ad A,86 prefer Ad B,and 60 prefer Ad C.The probability or proportion of participants preferring Ad B is
A).86
B).60
C).43
D)86
A).86
B).60
C).43
D)86

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
7
A researcher records the following data for the number of bids made on a sample of items sold at an auction.Based on the table,what was the probability that an item had 7 bids made on it? 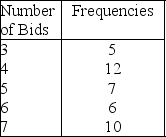
A)5
B)10
C).10
D).25

A)5
B)10
C).10
D).25

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is NOT a characteristic of probability?
A)Probability varies between 0 and 1.
B)Probability can never be negative.
C)Probability can be stated as a fraction or decimal.
D)Probability is most useful for describing fixed events.
A)Probability varies between 0 and 1.
B)Probability can never be negative.
C)Probability can be stated as a fraction or decimal.
D)Probability is most useful for describing fixed events.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
9
A researcher visits a population of 1,200 local residents to determine the proportion of local residents who support a new smoking ban.In this case,the sample space is
A)equal to the number of residents who support the new smoking ban
B)equal to the total number (or population)of residents
C)equal to more than just these 1,200 residents
D)unknown
A)equal to the number of residents who support the new smoking ban
B)equal to the total number (or population)of residents
C)equal to more than just these 1,200 residents
D)unknown

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
10
The following are six random outcomes for a sample space: -1,-3,-3,-2,-5,and -6.What is the probability of selecting a -3 in this example?
A)1/6
B)2/6
C)-2/6
D)-3/6
A)1/6
B)2/6
C)-2/6
D)-3/6

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
11
Which rule states that when two outcomes are mutually exclusive,the probability that either one of these outcomes will occur is the sum of their individual probabilities?
A)additive rule
B)multiplicative rule
C)both A and B
D)none of the above
A)additive rule
B)multiplicative rule
C)both A and B
D)none of the above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
12
Probability allows us to make predictions regarding:
A)random events
B)random outcomes
C)random variables
D)all of the above
A)random events
B)random outcomes
C)random variables
D)all of the above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
13
A therapist goes through her records and finds that 200 of her 400 patients showed significant improvement in mental health over the past year.Hence,the probability of her patients showing significant improvement in mental health is
A).05
B).50
C)200
D)400
A).05
B).50
C)200
D)400

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
14
If there are 13 heart cards in a deck of 52 cards,then what is the probability of selecting one heart card on a single draw from the deck of cards?
A)13/52
B)1/52
C)26/52
D)1/13
A)13/52
B)1/52
C)26/52
D)1/13

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
15
A news poll showed that voters had no preference for either of three candidates.In this example,the probability of a vote for,say,Candidate A equals
A)1/2
B)1/3
C)2/3
D)1.00
A)1/2
B)1/3
C)2/3
D)1.00

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
16
By definition,the probability of an outcome or event is
A)the proportion of times an outcome is likely to occur
B)the fraction of times an outcome is likely to occur
C)particularly useful for predicting the likelihood of random events
D)all of the above
A)the proportion of times an outcome is likely to occur
B)the fraction of times an outcome is likely to occur
C)particularly useful for predicting the likelihood of random events
D)all of the above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
17
The probability that someone in the human population has blood type AB is about p = .08;the probability that someone has blood type O is about p = .25.Knowing that each individual can have one and only one blood type,what is the probability that a person has an AB or O blood type?
A).33
B).02
C)1.00
D)This state of affairs is not possible.
A).33
B).02
C)1.00
D)This state of affairs is not possible.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
18
In a game,the probability of winning money is p = .16,the probability of losing money is p = .54,and the probability of breaking even is p = .30.What is the probability of winning or losing money in this game?
A).16
B).54
C).70
D)1.00
A).16
B).54
C).70
D)1.00

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
19
The total number of possible outcomes for a random variable is referred to as
A)probability
B)a random event
C)the sample space
D)the sum
A)probability
B)a random event
C)the sample space
D)the sum

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
20
A researcher finds that 20 of 120 students failed an exam.In this case,the probability of failing this exam was
A).14
B).17
C).20
D)unknown
A).14
B).17
C).20
D)unknown

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
21
The probability of a student attending every college class is p = .26.The probability of a student attending every college class and earning an A is p = .22.Hence,the probability of a student earning an A,given that he or she attends every college class,is
A)p = .06
B)p = .48
C)p = .85
D)There is not enough information to answer this question.
A)p = .06
B)p = .48
C)p = .85
D)There is not enough information to answer this question.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
22
A researcher records the number of job openings among small businesses.She finds that the probability that a small business has 0 job openings is p = .22;1 job opening is p = .45;2 job openings is p = .08;and 3 job openings is p = .25.What is the probability that a small business has at least 2 job openings?
A).08
B).25
C).33
D).67
A).08
B).25
C).33
D).67

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
23
When the sum of the probabilities of two outcomes is exhaustive of all possible outcomes,these outcomes are referred to as
A)mutually exclusive
B)complementary
C)independent
D)conditional
A)mutually exclusive
B)complementary
C)independent
D)conditional

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
24
The probability of a team having a sellout crowd is p = .45.The probability of having a sellout crowd and the team winning is p = .32.Hence,the probability of a team winning,given that they have a sellout crowd,is
A)p = .71
B)p = .77
C)p = .14
D)There is not enough information to answer this question.
A)p = .71
B)p = .77
C)p = .14
D)There is not enough information to answer this question.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
25
Suppose you open a new game at the county fair.When patrons win,you pay them $3.00;when patrons lose,they pay you $1.00.If the probability of a patron winning is p = .20,then how much can you expect to win (or lose)in the long run? Hint: You need to compute the expected value of the mean.
A)win 0.20 cents per play
B)win 0.60 cents per play
C)lose 0.80 cents per play
D)lose 2.20 dollars per play
A)win 0.20 cents per play
B)win 0.60 cents per play
C)lose 0.80 cents per play
D)lose 2.20 dollars per play

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
26
A professor records the grades for his class of students.He finds that the probability that a student earns an A is p = .14;earns a B is p = .36;earns a C is p = .32;earns a D is p = .10;and earns an F is p = .08.What is the probability that a student earns a B or better in this class?
A).36
B).14
C).86
D).50
A).36
B).14
C).86
D).50

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following is a mathematical formula that relates the conditional and marginal (unconditional)probabilities of two conditional outcomes that occur at random?
A)Bayes' theorem
B)simple probability
C)random event sampling
D)descriptive statistics
A)Bayes' theorem
B)simple probability
C)random event sampling
D)descriptive statistics

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
28
Which rule states that when two outcomes are independent,the probability that these outcomes occur together is the product of their individual probabilities?
A)additive rule
B)multiplicative rule
C)both A and B
D)none the of above
A)additive rule
B)multiplicative rule
C)both A and B
D)none the of above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
29
Bayes' theorem is often applied to a variety of ________ probability situations,including those related to statistical inference.
A)generic
B)absolute
C)conditional
D)fixed
A)generic
B)absolute
C)conditional
D)fixed

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
30
The distribution of probabilities for each outcome of a random variable that sums to 1.00 is called a
A)random variable
B)probability distribution
C)conditional probability
D)sample space
A)random variable
B)probability distribution
C)conditional probability
D)sample space

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose that the probability that any child of alcoholic parents becomes alcoholic is p = .16.Assuming independent outcomes,the probability that two children of alcoholic parents will be alcoholic equals
A).16
B).32
C).25
D).03
A).16
B).32
C).25
D).03

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
32
Below is the probability distribution for random variable x.What is the probability of at least a score of 2 in this distribution? 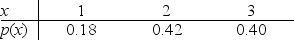
A).18
B).42
C).60
D).82
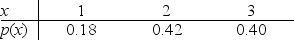
A).18
B).42
C).60
D).82

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
33
When the probability of one outcome changes depending on the occurrence of a second outcome,these outcomes are referred to as
A)mutually exclusive
B)complementary
C)independent
D)conditional
A)mutually exclusive
B)complementary
C)independent
D)conditional

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
34
Below is the probability distribution for random variable x.Which of the following is most probable? 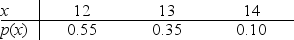
A)a score of at most 13
B)a score of at least 13
C)a score of 12
D)a score of 14
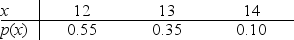
A)a score of at most 13
B)a score of at least 13
C)a score of 12
D)a score of 14

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
35
The probability of a college student being employed is p = .35.The probability of a student being employed and dropping out of college is p = .20.Hence,the probability of a student dropping out of college,given that he or she is employed,is
A)p = .07
B)p = .57
C)p = .55
D)There is not enough information to answer this question.
A)p = .07
B)p = .57
C)p = .55
D)There is not enough information to answer this question.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
36
A researcher records the number of mistakes made during a memory skills task.He finds that the probability that participants in this study made 0 mistakes is p = .22;made 1 mistake is p = .30;made 2 mistakes is p = .16;made 3 mistakes is p = .12;and made 4 or more mistakes is p = .25.Is this probability distribution accurate?
A)Yes,it distributes all possible outcomes for the random variable.
B)No,one of the outcomes is stated as "or more."
C)No,the probability distribution does not sum to 1.0.
D)both B and C
A)Yes,it distributes all possible outcomes for the random variable.
B)No,one of the outcomes is stated as "or more."
C)No,the probability distribution does not sum to 1.0.
D)both B and C

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
37
Below is the probability distribution for the number of times students had to take the same exam before passing it.If a student must pass the exam in two tries of less to pass the class,then what is the probability of passing the class? 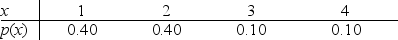
A).80
B).40
C).20
D).10
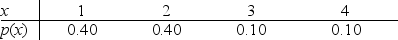
A).80
B).40
C).20
D).10

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
38
The probability that a parent rewards a child with a dessert for eating a healthy meal is .07.Assuming independent outcomes,the probability that two parents reward their child's healthy eating equals
A).07
B).14
C).05
D).005
A).07
B).14
C).05
D).005

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following probability distributions is accurate?
A)45/80,20/80,20/80,10/80
B)10/80,23/80,37/80,10/80
C)ñ20/80,40/80,40/80,20/80
D)none of the above
A)45/80,20/80,20/80,10/80
B)10/80,23/80,37/80,10/80
C)ñ20/80,40/80,40/80,20/80
D)none of the above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
40
The mean of a probability distribution is called the
A)expected value of the mean
B)mathematical expectation
C)both A and B
D)none of the above
A)expected value of the mean
B)mathematical expectation
C)both A and B
D)none of the above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
41
A researcher determines that the probability of missing class among students at a local school is p = .16.Assuming that the school has 300 students enrolled,how many students can we expect to miss class on a given day? Hint: This is a binomial probability distribution.
A)252 students
B)48 students
C)16 students
D)There is not enough information to answer this question.
A)252 students
B)48 students
C)16 students
D)There is not enough information to answer this question.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
42
A researcher reports that the probability of a college student living on campus is p = .38.If a small local college has 2,000 students enrolled,then what is the standard deviation of college students living on campus? Hint: This is a binomial probability distribution.
A)471.2 students
B)21.7 students
C)760 students
D)There is not enough information to answer this question.
A)471.2 students
B)21.7 students
C)760 students
D)There is not enough information to answer this question.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
43
A researcher records the number of buckets of popcorn purchased by patrons during one night at the movies.She finds that the probability that a patron purchased 0 buckets of popcorn is p = .27;1 bucket is p = .51;2 buckets is p = .17;and 3 buckets is p = .05.How many buckets of popcorn can we expect a patron to purchase per night at the movies in the long run?
A)exactly 1 bucket of popcorn per night
B)more than 1 bucket of popcorn per night
C)less than one bucket of popcorn per night
D)none of the above
A)exactly 1 bucket of popcorn per night
B)more than 1 bucket of popcorn per night
C)less than one bucket of popcorn per night
D)none of the above

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
44
The probability of an outcome can be any positive value.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
45
Each of the following is an example of a binomial distribution,except
A)the number of heads in ten flips of a fair coin
B)the number of males and females in a sample
C)the number of votes for or against a candidate
D)the time it takes to complete a driving test
A)the number of heads in ten flips of a fair coin
B)the number of males and females in a sample
C)the number of votes for or against a candidate
D)the time it takes to complete a driving test

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
46
A researcher determines that the relative frequency of participants with prescription glasses is .23.Hence,the probability that participants will wear prescription glasses must be greater than p = .23.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
47
The relative frequency of an outcome is the probability of its occurrence.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
48
Below is the probability distribution for the number of times students had to take the same exam before passing it.What is the value at the second standard deviation above the mean for this probability distribution? 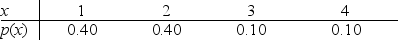
A)3.10
B)3.40
C)3.90
D)3.79
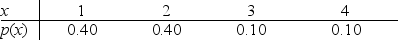
A)3.10
B)3.40
C)3.90
D)3.79

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
49
If a complimentary outcome has a 1 in 10 chance of occurrence,then the probability of that outcome is p = .10.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
50
If the variance of a probability distribution is 121,then the standard deviation is
A)121
B)21
C)12
D)11
A)121
B)21
C)12
D)11

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
51
Below is the probability distribution for random variable x.What is the standard deviation of this probability distribution? 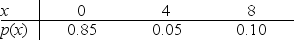
A)6.20
B)2.49
C)1.00
D)0.35
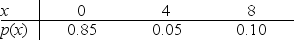
A)6.20
B)2.49
C)1.00
D)0.35

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
52
Probability ranges between 0 and 1 and is never negative.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
53
The sample space is equal to the total number of random outcomes possible for a random variable.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
54
If an outcome has a 1 in 100 chance of occurrence,then the probability of that outcome is p = .10.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
55
A probability can be stated as a proportion.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
56
If the standard deviation of a probability distribution is 9,then the variance is
A)3
B)9
C)81
D)unknown
A)3
B)9
C)81
D)unknown

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
57
The probability of an outcome is particularly useful for predicting the likelihood of fixed events.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
58
A distribution of probabilities for random outcomes of a bivariate or dichotomous random variable is called a
A)binomial probability distribution
B)distribution of expected values
C)random variable distribution
D)mathematical expectation
A)binomial probability distribution
B)distribution of expected values
C)random variable distribution
D)mathematical expectation

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
59
For mutually exclusive outcomes,one or the other outcome can occur (Outcome A or Outcome B),but not both outcomes (Outcome A and Outcome B)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
60
Below is the probability distribution for random variable x.What is the standard deviation of this probability distribution? 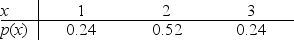
A)0.48
B)0.69
C)0.24
D)2.00
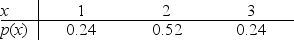
A)0.48
B)0.69
C)0.24
D)2.00

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
61
The expected value of a random variable is the mean of a probability distribution.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
62
The following probability distribution for outcomes 0,1,2,and 3,respectively,is possible: 18/30,3/30,4/30,and 5/30.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
63
While the expected value of the mean estimates the average outcome,the standard deviation of a probability distribution estimates the distance that all other outcomes deviate from the mean.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
64
Two outcomes are mutually exclusive when the probability of one outcome does not affect the probability of the second outcome.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
65
The multiplicative rule is used for independent outcomes.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
66
Conditional outcomes refer to those where the probability of one outcome is independent of the probability of the occurrence of the second outcome.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
67
The multiplicative rule is used to define mutually exclusive outcomes.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
68
A binomial probability distribution is constructed for random variables that have at least two possible outcomes.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
69
Bayes' theorem is a conditional probability formula.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
70
A researcher states that the probability of getting into an accident on a busy road is .09.Hence,the probability of getting into an accident twice on a busy road is .18.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
71
Probability distributions display the probability of each possible outcome for a given random variable.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
72
Bayes' theorem is most often applied to situations in which probability is not calculated.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
73
The probability distribution is p = .24,.16,.40,and .20 for a random variable with outcomes equal to 0,1,2,or 3,respectively.In this example,the expected value of the mean is greater than two.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
74
Bayes' theorem is often applied to a variety of conditional probability situations,including those related to statistical inference.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
75
The probability that a participant is married is p(M)= .60.The probability that a participant is married and "in love" is p(M L)= .46.Thus,the probability that a participant is in love,given that the participant is married is p = .77.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
76
The expected value of a random variable can be thought of as a "long-term" mean.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
77
Complementary outcomes are exhaustive of all possible outcomes.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
78
Mathematical expectation can be used to estimate the expected value of variance and standard deviation.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
79
Probability distributions follow the same rules as probability: They are never negative and vary between - ∞ and + 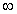 .
.
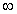 .
.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
80
The mean of a binomial distribution is the product of the number of trials (n)times the probability of the outcome of interest on an individual trial (p).

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck


