Exam 5: Probability, Normal Distributions, and Z Scores
Exam 1: Introduction to Statistics80 Questions
Exam 2: Summarizing Data: Frequency Distributions in80 Questions
Exam 3: Summarizing Data: Central Tendency80 Questions
Exam 4: Summarizing Data: Variability80 Questions
Exam 5: Probability, Normal Distributions, and Z Scores80 Questions
Exam 6: Characteristics of the Sample Mean79 Questions
Exam 7: Hypothesis Testing: Significance, Effect Size, and Power79 Questions
Exam 8: Testing Means: One-Sample T Test With Confidence Intervals80 Questions
Exam 9: Testing Means: Two- Independent-Sample T Test With Confidence Intervals76 Questions
Exam 10: Testing Means: Related-Samples T Test With Confidence Intervals79 Questions
Exam 11: One-Way Analysis of Variance: Between- Subjects and Within- Subjects Repeated- Measures Designs60 Questions
Exam 12: Two-Way Analysis of Variance: Between-Subjects Factorial Design80 Questions
Exam 13: Correlation and Linear Regression80 Questions
Exam 14: Chi-Square Tests: Goodness of Fit and the Test for Independence78 Questions
Exam 15: Nonparametric Tests for Ordinal Data: Understanding and Interpretation59 Questions
Exam 16: Chi-Square Tests: Goodness-of-Fit and Independence80 Questions
Exam 17: Understanding Regression Analysis80 Questions
Exam 18: Understanding Correlation Coefficients in Statistical Analysis80 Questions
Select questions type
Probability ranges between 0 and 1 and is never negative.
Free
(True/False)
4.9/5  (27)
(27)
Correct Answer:
True
A distribution of probabilities for random outcomes of a bivariate or dichotomous random variable is called a
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
A
If an outcome has a 1 in 100 chance of occurrence,then the probability of that outcome is p = .10.
Free
(True/False)
4.8/5  (26)
(26)
Correct Answer:
False
Bayes' theorem is often applied to a variety of conditional probability situations,including those related to statistical inference.
(True/False)
5.0/5  (33)
(33)
A binomial probability distribution is constructed for random variables that have at least two possible outcomes.
(True/False)
4.8/5  (32)
(32)
Probability distributions follow the same rules as probability: They are never negative and vary between - ∞ and + 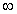 .
.
(True/False)
4.9/5  (34)
(34)
Mathematical expectation can be used to estimate the expected value of variance and standard deviation.
(True/False)
4.9/5  (35)
(35)
The mean of a binomial distribution is the product of the number of trials (n)times the probability of the outcome of interest on an individual trial (p).
(True/False)
4.8/5  (27)
(27)
Which of the following probability distributions is accurate?
(Multiple Choice)
4.8/5  (28)
(28)
The distribution of probabilities for each outcome of a random variable that sums to 1.00 is called a
(Multiple Choice)
4.9/5  (23)
(23)
The probability distribution is p = .24,.16,.40,and .20 for a random variable with outcomes equal to 0,1,2,or 3,respectively.In this example,the expected value of the mean is greater than two.
(True/False)
4.8/5  (26)
(26)
Bayes' theorem is most often applied to situations in which probability is not calculated.
(True/False)
4.9/5  (29)
(29)
The probability that a participant is married is p(M)= .60.The probability that a participant is married and "in love" is p(M L)= .46.Thus,the probability that a participant is in love,given that the participant is married is p = .77.
(True/False)
4.8/5  (35)
(35)
A researcher states that the probability of getting into an accident on a busy road is .09.Hence,the probability of getting into an accident twice on a busy road is .18.
(True/False)
4.8/5  (34)
(34)
The probability of an outcome is particularly useful for predicting the likelihood of fixed events.
(True/False)
4.8/5  (34)
(34)
A researcher finds that 20 of 120 students failed an exam.In this case,the probability of failing this exam was
(Multiple Choice)
4.9/5  (31)
(31)
Which of the following is a mathematical formula that relates the conditional and marginal (unconditional)probabilities of two conditional outcomes that occur at random?
(Multiple Choice)
4.9/5  (29)
(29)
Below is the probability distribution for random variable x.What is the probability of at least a score of 2 in this distribution? 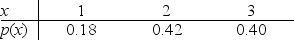
(Multiple Choice)
4.9/5  (40)
(40)
Suppose you open a new game at the county fair.When patrons win,you pay them $3.00;when patrons lose,they pay you $1.00.If the probability of a patron winning is p = .20,then how much can you expect to win (or lose)in the long run? Hint: You need to compute the expected value of the mean.
(Multiple Choice)
4.9/5  (32)
(32)
Showing 1 - 20 of 80
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)