Deck 15: Oscillations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/62
Play
Full screen (f)
Deck 15: Oscillations
1
An object attached to one end of a spring makes 20 vibrations in 10s. Its period is:
A) 2 Hz
B) 10 s
C) 0.5 Hz
D) 2 s
E) 0.50 s
A) 2 Hz
B) 10 s
C) 0.5 Hz
D) 2 s
E) 0.50 s
0.50 s
2
A particle moves back and forth along the x axis from x = -xm to x = +xm, in simple harmonic motion with period T. At time t = 0 it is at x = +xm. When t = 0.75T:
A) it is at x = 0 and is traveling toward x = +xm
B) it is at x = 0 and is traveling toward x = -xm
C) it is at x = +xm and is at rest
D) it is between x = 0 and x = +xm and is traveling toward x = -xm
E) it is between x = 0 and x = -xm and is traveling toward x = -xm
A) it is at x = 0 and is traveling toward x = +xm
B) it is at x = 0 and is traveling toward x = -xm
C) it is at x = +xm and is at rest
D) it is between x = 0 and x = +xm and is traveling toward x = -xm
E) it is between x = 0 and x = -xm and is traveling toward x = -xm
it is at x = 0 and is traveling toward x = +xm
3
An object is undergoing simple harmonic motion. Throughout a complete cycle it:
A) has constant speed
B) has varying amplitude
C) has varying period
D) has varying acceleration
E) has varying mass
A) has constant speed
B) has varying amplitude
C) has varying period
D) has varying acceleration
E) has varying mass
has varying acceleration
4
In simple harmonic motion, the magnitude of the acceleration is greatest when:
A) the displacement is zero
B) the displacement is maximum
C) the speed is maximum
D) the force is zero
E) the speed is between zero and its maximum
A) the displacement is zero
B) the displacement is maximum
C) the speed is maximum
D) the force is zero
E) the speed is between zero and its maximum

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
5
The amplitude of any oscillator can be doubled by:
A) doubling only the initial displacement
B) doubling only the initial speed
C) doubling the initial displacement and halving the initial speed
D) doubling the initial speed and halving the initial displacement
E) doubling both the initial displacement and the initial speed
A) doubling only the initial displacement
B) doubling only the initial speed
C) doubling the initial displacement and halving the initial speed
D) doubling the initial speed and halving the initial displacement
E) doubling both the initial displacement and the initial speed

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
6
An object attached to one end of a spring makes 20 vibrations in 10 seconds. Its frequency is:
A) 2 Hz
B) 10 s
C) 0.05 Hz
D) 2 s
E) 0.50 s
A) 2 Hz
B) 10 s
C) 0.05 Hz
D) 2 s
E) 0.50 s

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
7
Frequency f and angular frequency are related by
A) f =
B) f = 2
C) f = /
D) f = /2
E) f = 2 /
A) f =
B) f = 2
C) f = /
D) f = /2
E) f = 2 /

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
8
An oscillatory motion must be simple harmonic if:
A) the amplitude is small
B) the potential energy is equal to the kinetic energy
C) the motion is along the arc of a circle
D) the acceleration varies sinusoidally with time
E) the derivative, dU/dx, of the potential energy is negative
A) the amplitude is small
B) the potential energy is equal to the kinetic energy
C) the motion is along the arc of a circle
D) the acceleration varies sinusoidally with time
E) the derivative, dU/dx, of the potential energy is negative

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
9
In simple harmonic motion:
A) the acceleration is greatest at the maximum displacement
B) the velocity is greatest at the maximum displacement
C) the period depends on the amplitude
D) the acceleration is constant
E) the acceleration is greatest at zero displacement
A) the acceleration is greatest at the maximum displacement
B) the velocity is greatest at the maximum displacement
C) the period depends on the amplitude
D) the acceleration is constant
E) the acceleration is greatest at zero displacement

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
10
A weight suspended from an ideal spring oscillates up and down with a period T. If the amplitude of the oscillation is doubled, the period will be:
A) T
B) 1.5 T
C) 2T
D) T/2
E) 4T
A) T
B) 1.5 T
C) 2T
D) T/2
E) 4T

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
11
The amplitude and phase constant of an oscillator are determined by:
A) the frequency
B) the angular frequency
C) the initial displacement alone
D) the initial velocity alone
E) both the initial displacement and velocity
A) the frequency
B) the angular frequency
C) the initial displacement alone
D) the initial velocity alone
E) both the initial displacement and velocity

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
12
In simple harmonic motion, the displacement is maximum when the:
A) acceleration is zero
B) velocity is maximum
C) velocity is zero
D) kinetic energy is maximum
E) momentum is maximum
A) acceleration is zero
B) velocity is maximum
C) velocity is zero
D) kinetic energy is maximum
E) momentum is maximum

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
13
A particle oscillating in simple harmonic motion is:
A) never in equilibrium because it is in motion
B) never in equilibrium because there is a force
C) in equilibrium at the ends of its path because its velocity is zero there
D) in equilibrium at the center of its path because the acceleration is zero there
E) in equilibrium at the ends of its path because the acceleration is zero there
A) never in equilibrium because it is in motion
B) never in equilibrium because there is a force
C) in equilibrium at the ends of its path because its velocity is zero there
D) in equilibrium at the center of its path because the acceleration is zero there
E) in equilibrium at the ends of its path because the acceleration is zero there

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
14
An object attached to one end of a spring makes 20 vibrations in 10 seconds. Its angular frequency is:
A) 0.79 rad/s
B) 1.57 rad/s
C) 2.0 rad/s
D) 6.3 rad/s
E) 12.6 rad/s
A) 0.79 rad/s
B) 1.57 rad/s
C) 2.0 rad/s
D) 6.3 rad/s
E) 12.6 rad/s

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
15
In simple harmonic motion, the magnitude of the acceleration is:
A) constant
B) proportional to the displacement
C) inversely proportional to the displacement
D) greatest when the velocity is greatest
E) never greater than g
A) constant
B) proportional to the displacement
C) inversely proportional to the displacement
D) greatest when the velocity is greatest
E) never greater than g

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
16
A particle is in simple harmonic motion with period T. At time t=0 it is halfway between the equilibrium point and an end point of its motion, travelling toward the end point. The next time it is at the same place is:
A) t = T
B) t = T/2
C) t = T/4
D) t = T/8
E) none of the above
A) t = T
B) t = T/2
C) t = T/4
D) t = T/8
E) none of the above

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
17
A block attached to a spring oscillates in simple harmonic motion along the x axis. The limits of its motion are x = 10 cm and x = 50 cm and it goes from one of these extremes to the other in 0.25 s. Its amplitude and frequency are:
A) 40 cm, 2 Hz
B) 20 cm, 4 Hz
C) 40 cm, 1 Hz
D) 25 cm, 4 Hz
E) 20 cm, 2 Hz
A) 40 cm, 2 Hz
B) 20 cm, 4 Hz
C) 40 cm, 1 Hz
D) 25 cm, 4 Hz
E) 20 cm, 2 Hz

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
18
When a body executes simple harmonic motion, its acceleration at the ends of its path must be:
A) zero
B) less than g
C) more than g
D) suddenly changing in sign
E) none of these
A) zero
B) less than g
C) more than g
D) suddenly changing in sign
E) none of these

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
19
Two identical undamped oscillators have the same amplitude of oscillation only if:
A) they are started with the same displacement x0
B) they are started with the same velocity v0
C) they are started with the same phase
D)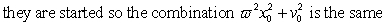
E)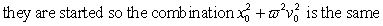
A) they are started with the same displacement x0
B) they are started with the same velocity v0
C) they are started with the same phase
D)
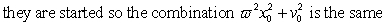
E)
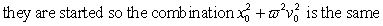

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
20
A particle is in simple harmonic motion with period T. At time t = 0 it is at the equilibrium point. At which of the following times is it furthest from the equilibrium point?
A) 0.5T
B) 0.7T
C) T
D) 1.4T
E) 1.5T
A) 0.5T
B) 0.7T
C) T
D) 1.4T
E) 1.5T

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
21
A 0.20-kg object mass attached to a spring whose spring constant is 500 N/m executes simple harmonic motion. If its maximum speed is 5.0 m/s, the amplitude of its oscillation is:
A) 0.0020 m
B) 0.10 m
C) 0.20 m
D) 25 m
E) 250 m
A) 0.0020 m
B) 0.10 m
C) 0.20 m
D) 25 m
E) 250 m

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
22
Let U be the potential energy (with the zero at zero displacement) and K be the kinetic energy of a simple harmonic oscillator. Uavg and Kavg are the average values over a cycle. Then:
A) Kavg > Uavg
B) Kavg < Uavg
C) Kavg = Uavg
D) K = 0 when U = 0
E) K + U = 0
A) Kavg > Uavg
B) Kavg < Uavg
C) Kavg = Uavg
D) K = 0 when U = 0
E) K + U = 0

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
23
A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the oscillation is started by elongating the spring 0.15 m and giving the block a speed of 3.0 m/s, then the maximum speed of the block is:
A) 0.13 m/s
B) 0.18 m/s
C) 3.7 m/s
D) 5.2 m/s
E) 13 m/s
A) 0.13 m/s
B) 0.18 m/s
C) 3.7 m/s
D) 5.2 m/s
E) 13 m/s

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
24
An object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. Its maximum speed is:
A)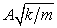
B) A2k/m
C)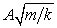
D) Am/k
E) A2m/k
A)
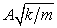
B) A2k/m
C)
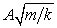
D) Am/k
E) A2m/k

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
25
A simple harmonic oscillator consists of a mass m and an ideal spring with spring constant k. The particle oscillates as shown in (i) with period T. If the spring is cut in half and used with the same particle, as shown in (ii), the period will be: 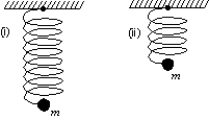
A) 2T
B)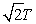
C)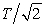
D) T
E) T/2

A) 2T
B)
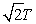
C)
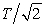
D) T
E) T/2

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
26
The displacement of an object oscillating on a spring is given by x(t) = xmcos( t + ). If the initial displacement is zero and the initial velocity is in the negative x direction, then the phase constant is:
A) 0
B) /2 radians
C) radians
D) 3 /2 radians
E) 2 radians
A) 0
B) /2 radians
C) radians
D) 3 /2 radians
E) 2 radians

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
27
A certain spring elongates 9 mm when it is suspended vertically and a block of mass M is hung on it. The natural frequency of this mass-spring system is:
A) is 0.088 rad/s
B) is 33 rad/s
C) is 200 rad/s
D) is 1140 rad/s
E) cannot be computed unless the value of M is given
A) is 0.088 rad/s
B) is 33 rad/s
C) is 200 rad/s
D) is 1140 rad/s
E) cannot be computed unless the value of M is given

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
28
In simple harmonic motion, the restoring force must be proportional to the:
A) amplitude
B) frequency
C) velocity
D) displacement
E) displacement squared
A) amplitude
B) frequency
C) velocity
D) displacement
E) displacement squared

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
29
A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the oscillation is started by elongating the spring 0.15 m and giving the block a speed of 3.0 m/s, then the amplitude of the oscillation is:
A) 0.13 m
B) 0.18 m
C) 3.7 m
D) 5.2 m
E) 13 m
A) 0.13 m
B) 0.18 m
C) 3.7 m
D) 5.2 m
E) 13 m

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
30
A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the system has an energy of 6.0 J, then the maximum speed of the block is:
A) 0.06 m/s
B) 0.17 m/s
C) 0.24 m/s
D) 4.9 m/s
E) 6.9 m/s
A) 0.06 m/s
B) 0.17 m/s
C) 0.24 m/s
D) 4.9 m/s
E) 6.9 m/s

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
31
The acceleration of a body executing simple harmonic motion leads the velocity by what phase?
A) 0
B) /8 rad
C) /4 rad
D) /2 rad
E) rad
A) 0
B) /8 rad
C) /4 rad
D) /2 rad
E) rad

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
32
A particle moves in simple harmonic motion according to x = 2cos(50t), where x is in meters and t is in seconds. Its maximum velocity in m/s is:
A) 100 sin(50t)
B) 100 cos(50t)
C) 100
D) 200
E) none of these
A) 100 sin(50t)
B) 100 cos(50t)
C) 100
D) 200
E) none of these

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
33
A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the system has an energy of 6.0 J, then the amplitude of the oscillation is:
A) 0.06 m
B) 0.17 m
C) 0.24 m
D) 4.9 m
E) 6.9 m
A) 0.06 m
B) 0.17 m
C) 0.24 m
D) 4.9 m
E) 6.9 m

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
34
A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. When it is at x = x1, its kinetic energy is K = 5J and its potential energy (measured with U = 0 at x = 0) is U = 3J. When it is at x = -1/2xm, the kinetic and potential energies are:
A) K = 5J and U = 3J
B) K = 5J and U = -3J
C) K = 8J and U = 0
D) K = 0 and U = 8J
E) K = 0 and U = -8J
A) K = 5J and U = 3J
B) K = 5J and U = -3J
C) K = 8J and U = 0
D) K = 0 and U = 8J
E) K = 0 and U = -8J

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
35
A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. At one point in its motion its kinetic energy is K = 5J and its potential energy (measured with U = 0 at x = 0) is U = 3J. When it is at x = xm, the kinetic and potential energies are:
A) K = 5J and U = 3J
B) K = 5J and U = -3J
C) K = 8J and U = 0
D) K = 0 and U = 8J
E) K = 0 and U = -8J
A) K = 5J and U = 3J
B) K = 5J and U = -3J
C) K = 8J and U = 0
D) K = 0 and U = 8J
E) K = 0 and U = -8J

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
36
A block attached to a spring undergoes simple harmonic motion on a horizontal frictionless surface. Its total energy is 50 J. When the displacement is half the amplitude, the kinetic energy is:
A) zero
B) 12.5 J
C) 25 J
D) 37.5 J
E) 50 J
A) zero
B) 12.5 J
C) 25 J
D) 37.5 J
E) 50 J

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
37
The displacement of an object oscillating on a spring is given by x(t) = xmcos( t + ). If the object is initially displaced in the negative x direction and given a negative initial velocity, then the phase constant is between:
A) 0 and /2 radians
B) /2 and radians
C) and 3 /2 radians
D) 3 /2 and 2 radians
E) none of the above ( is exactly 0, /2, , or 3 /2 radians)
A) 0 and /2 radians
B) /2 and radians
C) and 3 /2 radians
D) 3 /2 and 2 radians
E) none of the above ( is exactly 0, /2, , or 3 /2 radians)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
38
A 3-kg block, attached to a spring, executes simple harmonic motion according to x = 2cos(50t) where x is in meters and t is in seconds. The spring constant of the spring is:
A) 1 N/m
B) 100 N/m
C) 150 N/m
D) 7500 N/m
E) none of these
A) 1 N/m
B) 100 N/m
C) 150 N/m
D) 7500 N/m
E) none of these

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
39
It is impossible for two particles, each executing simple harmonic motion, to remain in phase with each other if they have different:
A) masses
B) periods
C) amplitudes
D) spring constants
E) kinetic energies
A) masses
B) periods
C) amplitudes
D) spring constants
E) kinetic energies

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
40
An object on the end of a spring is set into oscillation by giving it an initial velocity while it is at its equilibrium position. In the first trial the initial velocity is v0 and in the second it is 4v0. In the second trial:
A) the amplitude is half as great and the maximum acceleration is twice as great
B) the amplitude is twice as great and the maximum acceleration is half as great
C) both the amplitude and the maximum acceleration are twice as great
D) both the amplitude and the maximum acceleration are four times as great
E) the amplitude is four times as great and the maximum acceleration is twice as great
A) the amplitude is half as great and the maximum acceleration is twice as great
B) the amplitude is twice as great and the maximum acceleration is half as great
C) both the amplitude and the maximum acceleration are twice as great
D) both the amplitude and the maximum acceleration are four times as great
E) the amplitude is four times as great and the maximum acceleration is twice as great

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
41
A simple pendulum has length L and period T. As it passes through its equilibrium position, the string is suddenly clamped at its mid-point. The period then becomes:
A) 2T
B) T
C) T/2
D) T/4
E) none of the above
A) 2T
B) T
C) T/2
D) T/4
E) none of the above

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
42
A meter stick is pivoted at a point a distance a from its center and swings as a physical pendulum. Of the following values for a, which results in the shortest period of oscillation?
A) a = 0.1 m
B) a = 0.2 m
C) a = 0.3 m
D) a = 0.4 m
E) a = 0.5 m
A) a = 0.1 m
B) a = 0.2 m
C) a = 0.3 m
D) a = 0.4 m
E) a = 0.5 m

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
43
Five particles undergo damped harmonic motion. Values for the spring constant k, the damping constant b, and the mass m are given below. Which leads to the smallest rate of loss of mechanical energy?
A) k = 100N/m, m = 50g, b = 8g/s
B) k = 150N/m, m = 50g, b = 5g/s
C) k = 150N/m, m = 10g, b = 8g/s
D) k = 200N/m, m = 8g, b = 6g/s
E) k = 100N/m, m = 2g, b = 4g/s
A) k = 100N/m, m = 50g, b = 8g/s
B) k = 150N/m, m = 50g, b = 5g/s
C) k = 150N/m, m = 10g, b = 8g/s
D) k = 200N/m, m = 8g, b = 6g/s
E) k = 100N/m, m = 2g, b = 4g/s

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
44
For an oscillator subjected to a damping force proportional to its velocity:
A) the displacement is a sinusoidal function of time
B) the velocity is a sinusoidal function of time
C) the frequency is a decreasing function of time
D) the mechanical energy is constant
E) none of the above is true
A) the displacement is a sinusoidal function of time
B) the velocity is a sinusoidal function of time
C) the frequency is a decreasing function of time
D) the mechanical energy is constant
E) none of the above is true

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
45
A sinusoidal force with a given amplitude is applied to an oscillator. To maintain the largest amplitude oscillation the frequency of the applied force should be:
A) half the natural frequency of the oscillator
B) the same as the natural frequency of the oscillator
C) twice the natural frequency of the oscillator
D) unrelated to the natural frequency of the oscillator
E) determined from the maximum speed desired
A) half the natural frequency of the oscillator
B) the same as the natural frequency of the oscillator
C) twice the natural frequency of the oscillator
D) unrelated to the natural frequency of the oscillator
E) determined from the maximum speed desired

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
46
A mass-spring system is oscillating with amplitude A. The kinetic energy will equal the potential energy only when the displacement is
A) zero
B) A/4
C)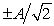
D) A/2
E) anywhere between -A and +A
A) zero
B) A/4
C)
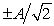
D) A/2
E) anywhere between -A and +A

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
47
Both the x and y coordinates of a point execute simple harmonic motion. The frequencies are the same but the amplitudes are different. The resulting orbit might be:
A) an ellipse
B) a circle
C) a parabola
D) a hyperbola
E) a square
A) an ellipse
B) a circle
C) a parabola
D) a hyperbola
E) a square

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
48
A simple pendulum consists of a small ball tied to a string and set in oscillation. As the pendulum swings the tension in the string is:
A) constant
B) a sinusoidal function of time
C) the square of a sinusoidal function of time
D) the reciprocal of a sinusoidal function of time
E) none of the above
A) constant
B) a sinusoidal function of time
C) the square of a sinusoidal function of time
D) the reciprocal of a sinusoidal function of time
E) none of the above

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
49
Three physical pendulums, with masses m1, m2 = 2m1, and m3 = 3m1, have the same shape and size and are suspended at the same point. Rank them according to their periods, from shortest to longest.
A) 1, 2, 3
B) 3, 2, 1
C) 2, 3, 1
D) 2, 1, 3
E) All the above are the same
A) 1, 2, 3
B) 3, 2, 1
C) 2, 3, 1
D) 2, 1, 3
E) All the above are the same

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
50
A simple pendulum of length L and mass M has frequency f. To increase its frequency to 2f:
A) increase its length by length to 4L
B) increase its length by length to 2L
C) decrease its length by length to L/2
D) decrease its length by length to L/ 4
E) decrease its mass by length to < M/4
A) increase its length by length to 4L
B) increase its length by length to 2L
C) decrease its length by length to L/2
D) decrease its length by length to L/ 4
E) decrease its mass by length to < M/4

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
51
Two uniform spheres are pivoted on horizontal axes that are tangent to their surfaces. The one with the longer period of oscillation is the one with:
A) the larger mass
B) the smaller mass
C) the larger rotational inertia
D) the smaller rotational inertia
E) the larger radius
A) the larger mass
B) the smaller mass
C) the larger rotational inertia
D) the smaller rotational inertia
E) the larger radius

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
52
An oscillator is subjected to a damping force that is proportional to its velocity. A sinusoidal force is applied to it. After a long time:
A) its amplitude is an increasing function of time
B) its amplitude is a decreasing function of time
C) its amplitude is constant
D) its amplitude is a decreasing function of time only if the damping constant is large
E) its amplitude increases over some portions of a cycle and decreases over other portions
A) its amplitude is an increasing function of time
B) its amplitude is a decreasing function of time
C) its amplitude is constant
D) its amplitude is a decreasing function of time only if the damping constant is large
E) its amplitude increases over some portions of a cycle and decreases over other portions

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
53
Five hoops are each pivoted at a point on the rim and allowed to swing as physical pendulums. The masses and radii are 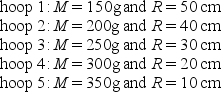 Order the hoops according to the periods of their motions, smallest to largest.
Order the hoops according to the periods of their motions, smallest to largest.
A) 1, 2, 3, 4, 5
B) 5, 4, 3, 2, 1
C) 1, 2, 3, 5, 4
D) 1, 2, 5, 4, 3
E) 5, 4, 1, 2, 3
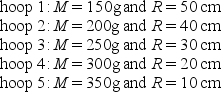 Order the hoops according to the periods of their motions, smallest to largest.
Order the hoops according to the periods of their motions, smallest to largest.A) 1, 2, 3, 4, 5
B) 5, 4, 3, 2, 1
C) 1, 2, 3, 5, 4
D) 1, 2, 5, 4, 3
E) 5, 4, 1, 2, 3

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
54
If the length of a simple pendulum is doubled, its period will:
A) halve
B)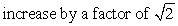
C)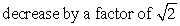
D) double
E) remain the same
A) halve
B)
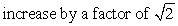
C)
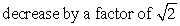
D) double
E) remain the same

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
55
The rotational inertia of a uniform thin rod about its end is ML2/3, where M is the mass and L is the length. Such a rod is hung vertically from one end and set into small amplitude oscillation. If L = 1.0 m this rod will have the same period as a simple pendulum of length:
A) 33 cm
B) 50 cm
C) 67 cm
D) 100 cm
E) 150 cm
A) 33 cm
B) 50 cm
C) 67 cm
D) 100 cm
E) 150 cm

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
56
Both the x and y coordinates of a point execute simple harmonic motion. The result might be a circular orbit if:
A) the amplitudes are the same but the frequencies are different
B) the amplitudes and frequencies are both the same
C) the amplitudes and frequencies are both different
D) the phase constants are the same but the amplitudes are different
E) the amplitudes and the phase constants are both different
A) the amplitudes are the same but the frequencies are different
B) the amplitudes and frequencies are both the same
C) the amplitudes and frequencies are both different
D) the phase constants are the same but the amplitudes are different
E) the amplitudes and the phase constants are both different

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
57
A simple pendulum is suspended from the ceiling of an elevator. The elevator is accelerating upwards with acceleration a. The period of this pendulum, in terms of its length L, g and a is:
A)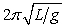
B)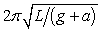
C)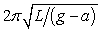
D)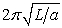
E)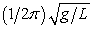
A)
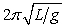
B)
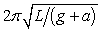
C)
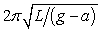
D)
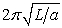
E)
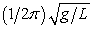

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
58
The period of a simple pendulum is 1 s on Earth. When brought to a planet where g is one-tenth that on Earth, its period becomes:
A) 1 s
B)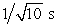
C) 1/10 s
D)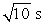
E) 10 s
A) 1 s
B)
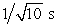
C) 1/10 s
D)
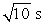
E) 10 s

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
59
A sinusoidal force with a given amplitude is applied to an oscillator. At resonance the amplitude of the oscillation is limited by:
A) the damping force
B) the initial amplitude
C) the initial velocity
D) the force of gravity
E) none of the above
A) the damping force
B) the initial amplitude
C) the initial velocity
D) the force of gravity
E) none of the above

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
60
The amplitude of oscillation of a simple pendulum is increased from 1 to 4 . Its maximum acceleration changes by a factor of:
A) 1/4
B) 1/2
C) 2
D) 4
E) 16
A) 1/4
B) 1/2
C) 2
D) 4
E) 16

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
61
A block on a spring is subjected to an applied sinusoidal force AND to a damping force that is proportional to its velocity. The energy dissipated by damping is supplied by:
A) the potential energy of the spring
B) the kinetic energy of the mass
C) gravity
D) friction
E) the applied force
A) the potential energy of the spring
B) the kinetic energy of the mass
C) gravity
D) friction
E) the applied force

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
62
Below are sets of values for the spring constant k, damping constant b, and mass m for a particle in damped harmonic motion. Which of the sets takes the longest time for its mechanical energy to decrease to one-fourth of its initial value? 
A)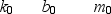
B)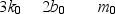
C)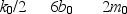
D)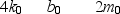
E)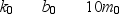
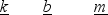
A)
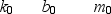
B)
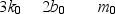
C)
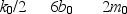
D)
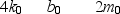
E)
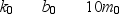

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck


