Exam 15: Oscillations
Exam 1: Measurement31 Questions
Exam 2: Motion Along a Straight Line79 Questions
Exam 3: Vector39 Questions
Exam 4: Motion in Two and Three Dimensions47 Questions
Exam 5: Force and Motion I68 Questions
Exam 6: Force and Motion II71 Questions
Exam 7: Kinetic Energy and Work67 Questions
Exam 8: Potential Energy and Conservation of Energy61 Questions
Exam 9: Center of Mass and Linear Momentum81 Questions
Exam 10: Rotation82 Questions
Exam 11: Rolling, Torque, and Angular Momentum54 Questions
Exam 12: Equilibrium and Elasticity53 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids85 Questions
Exam 15: Oscillations62 Questions
Exam 16: Waves I71 Questions
Exam 17: Waves II61 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics82 Questions
Exam 19: The Kinetic Theory of Gases95 Questions
Exam 20: Entropy and the Second Law of Thermodynamics56 Questions
Exam 21: Electric Charge45 Questions
Exam 22: Electric Fields49 Questions
Exam 23: Gauss Law34 Questions
Exam 24: Electric Potential44 Questions
Exam 25: Capacitance55 Questions
Exam 26: Current and Resistance49 Questions
Exam 27: Circuits70 Questions
Exam 28: Magnetic Fields48 Questions
Exam 29: Magnetic Fields Due to Currents47 Questions
Exam 30: Induction and Inductance85 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current84 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves79 Questions
Exam 34: Images72 Questions
Exam 35: Interference40 Questions
Exam 36: Diffraction74 Questions
Exam 37: Relativity65 Questions
Exam 38: Photons and Matter Waves53 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms76 Questions
Exam 41: Conduction of Electricity in Solids48 Questions
Exam 42: Nuclear Physics67 Questions
Exam 43: Energy From the Nucleus44 Questions
Exam 44: Quarks, Leptons, and the Big Bang52 Questions
Select questions type
A simple harmonic oscillator consists of a mass m and an ideal spring with spring constant k. The particle oscillates as shown in (i) with period T. If the spring is cut in half and used with the same particle, as shown in (ii), the period will be: 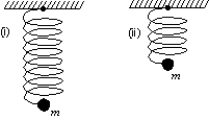
Free
(Multiple Choice)
4.9/5  (24)
(24)
Correct Answer:
C
A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. At one point in its motion its kinetic energy is K = 5J and its potential energy (measured with U = 0 at x = 0) is U = 3J. When it is at x = xm, the kinetic and potential energies are:
Free
(Multiple Choice)
4.7/5  (38)
(38)
Correct Answer:
D
The acceleration of a body executing simple harmonic motion leads the velocity by what phase?
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
D
A weight suspended from an ideal spring oscillates up and down with a period T. If the amplitude of the oscillation is doubled, the period will be:
(Multiple Choice)
4.7/5  (28)
(28)
A simple pendulum consists of a small ball tied to a string and set in oscillation. As the pendulum swings the tension in the string is:
(Multiple Choice)
4.7/5  (27)
(27)
A simple pendulum has length L and period T. As it passes through its equilibrium position, the string is suddenly clamped at its mid-point. The period then becomes:
(Multiple Choice)
4.9/5  (32)
(32)
Two identical undamped oscillators have the same amplitude of oscillation only if:
(Multiple Choice)
5.0/5  (34)
(34)
The displacement of an object oscillating on a spring is given by x(t) = xmcos( t + ). If the initial displacement is zero and the initial velocity is in the negative x direction, then the phase constant is:
(Multiple Choice)
4.8/5  (34)
(34)
It is impossible for two particles, each executing simple harmonic motion, to remain in phase with each other if they have different:
(Multiple Choice)
4.9/5  (28)
(28)
The amplitude of oscillation of a simple pendulum is increased from 1 to 4 . Its maximum acceleration changes by a factor of:
(Multiple Choice)
4.9/5  (37)
(37)
Below are sets of values for the spring constant k, damping constant b, and mass m for a particle in damped harmonic motion. Which of the sets takes the longest time for its mechanical energy to decrease to one-fourth of its initial value? 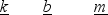
(Multiple Choice)
4.8/5  (32)
(32)
Two uniform spheres are pivoted on horizontal axes that are tangent to their surfaces. The one with the longer period of oscillation is the one with:
(Multiple Choice)
4.8/5  (28)
(28)
The rotational inertia of a uniform thin rod about its end is ML2/3, where M is the mass and L is the length. Such a rod is hung vertically from one end and set into small amplitude oscillation. If L = 1.0 m this rod will have the same period as a simple pendulum of length:
(Multiple Choice)
4.8/5  (26)
(26)
A mass-spring system is oscillating with amplitude A. The kinetic energy will equal the potential energy only when the displacement is
(Multiple Choice)
4.8/5  (28)
(28)
A sinusoidal force with a given amplitude is applied to an oscillator. To maintain the largest amplitude oscillation the frequency of the applied force should be:
(Multiple Choice)
4.7/5  (40)
(40)
In simple harmonic motion, the displacement is maximum when the:
(Multiple Choice)
4.9/5  (27)
(27)
An object is undergoing simple harmonic motion. Throughout a complete cycle it:
(Multiple Choice)
4.7/5  (26)
(26)
A simple pendulum of length L and mass M has frequency f. To increase its frequency to 2f:
(Multiple Choice)
4.8/5  (42)
(42)
A sinusoidal force with a given amplitude is applied to an oscillator. At resonance the amplitude of the oscillation is limited by:
(Multiple Choice)
4.7/5  (28)
(28)
Both the x and y coordinates of a point execute simple harmonic motion. The frequencies are the same but the amplitudes are different. The resulting orbit might be:
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)