Deck 17: the Simplex Solution Method
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/90
Play
Full screen (f)
Deck 17: the Simplex Solution Method
1
In using the simplex method, the number of basic variables is equal to the number of constraints.
True
2
Row operations are used to solve simultaneous equations where equations are multiplied by constants and added or subtracted from each other.
True
3
A basic feasible solution satisfies the model constraints and has the same number of variables with negative values as there are constraints.
False
4
The simplex method can be used to solve quadratic programming problems.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
5
A basic feasible solution satisfies the model constraints and has the same number of variables with non-negative values as there are constraints.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
6
The simplex method is a general mathematical solution technique for solving linear programming problems.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
7
The first step in solving a linear programming model manually with the simplex method is to convert the model into standard form.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
8
The simplex method cannot be used to solve quadratic programming problems.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
9
The simplex method moves from one better solution to another until the best one is found, and then it stops.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
10
The basic feasible solution in the initial simplex tableau is the origin where all decision variables equal zero.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
11
The simplex method does not guarantee an integer solution.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
12
At the initial basic feasible solution at the origin, only slack variables have a value greater than zero.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
13
The mathematical steps in the simplex method replicate the process in graphical analysis of moving from one extreme point on the solution boundary to another.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
14
The last step in solving a linear programming model manually with the simplex method is to convert the model into standard form.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
15
In solving a linear programming problem with simplex method, the number of basic variables is the same as the number of constraints in the original problem

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
16
Slack variables are added to constraints and represent unused resources.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
17
Artificial variables are added to constraints and represent unused resources.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
18
In the simplex method, the model is put into the form of a table, and then a number of mathematical steps are performed on the table.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
19
At the initial basic feasible solution at the origin, only slack variables have a value greater than 1.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
20
The simplex method is a general mathematical solution technique for solving nonlinear programming problems.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
21
Multiple optimal solutions cannot be determined from the simplex method.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
22
The variable with the largest positive cj - zj is the ________ variable.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
23
The theoretical limit on the number of decision variables that can be handled by the simplex method is 50.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
24
A(n) ________ maximization linear programming problem has an artificial variable in the final simplex tableau where all cj - zj values are less than or equal to zero.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
25
The dual form of a linear program is used to determine how much one should pay for additional resources.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
26
Whereas the maximization primal model has ≤ constraints, the ________ dual model has ≥ constraints.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
27
In using the simplex method, ________ optimal solutions are identified by cj - zj = 0 for a non-basic variable.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
28
If the primal problem has three constraints, then the corresponding dual problem will have three ________.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
29
The first step in solving a linear programming model manually with the simplex method is to convert the model into ________ form.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
30
When solving a linear programming problem, a decision variable that leaves the basis in one iteration of the simplex method can return to the basis on a later iteration.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
31
The ________ column is the column corresponding to the entering variable.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
32
A change in the objective function coefficient of a basic variable cannot change the value of zj for a non-basic variable in the final simplex tableau.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
33
The quantity values on the right-hand side of the primal inequality constraints are the ________ coefficients in the dual.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
34
A primal maximization model with ≤ constraints converts to a ________ minimization model with constraints.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
35
The ________ variable allows for an initial basic feasible solution, but it has no meaning. Therefore, after we get the simplex tableau started, they are discarded in later iterations.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
36
Final tableaus cannot be used to conduct sensitivity analysis.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
37
In solving a minimization problem, artificial variables are assigned a ________ in the objective function to eliminate them from the final solution.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
38
The ________ values are computed by multiplying the cj column values by the variable column values and summing.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
39
________ variables are added to constraints and represent unused resources.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
40
The ________ values are contribution to profit for each variable.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
41
Given the following linear programming problem:
What are the basic variables in the initial tableau?
What are the basic variables in the initial tableau?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
42
To determine the sensitivity range for the coefficient of a variable in the objective function, calculations are performed such that all values in the cj - zj row are ________.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
43
________ in linear programming is when a basic variable takes on a value of zero (i.e., a zero in the right-hand side of the constraints of the tableau).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
44
Given the following linear programming problem:
maximize Z = $100x1 + 80x2
subject to x1 + 2x2 ≤ 40
3x1 + x2 ≤ 60
x1, x2 ≥ 0
Using the simplex method, what is the optimal value for the objective function?
maximize Z = $100x1 + 80x2
subject to x1 + 2x2 ≤ 40
3x1 + x2 ≤ 60
x1, x2 ≥ 0
Using the simplex method, what is the optimal value for the objective function?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
45
Given the following linear programming problem:
Using the simplex method, what is the value for S1 in the final basic feasible solution?
Using the simplex method, what is the value for S1 in the final basic feasible solution?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
46
The ________ form of a linear program is used to determine how much one should pay for additional resources.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
47
Given the following linear programming problem:
maximize Z = $100x1 + 80x2
subject to x1 + 2x2 ≤ 40
3x1 + x2 ≤ 60
x1, x2 ≥ 0
Using the simplex method, what is the optimal value for X1?
maximize Z = $100x1 + 80x2
subject to x1 + 2x2 ≤ 40
3x1 + x2 ≤ 60
x1, x2 ≥ 0
Using the simplex method, what is the optimal value for X1?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
48
Given the following linear programming problem:
What are the Cj values for the basic variables?
What are the Cj values for the basic variables?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
49
A(n) ________ problem can be identified in the simplex procedure when it is not possible to select a pivot row.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
50
Given the following linear programming problem:
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
What is the value of X1 in the final tableau?
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
What is the value of X1 in the final tableau?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
51
In a ________ problem, artificial variables are assigned a very high cost.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
52
Given the following linear programming problem:
maximize Z = $100x1 + 80x2
subject to x1 + 2x2 ≤ 40
3x1 + x2 ≤ 60
x1, x2 ≥ 0
Using the simplex method, what is the optimal value for X2?
maximize Z = $100x1 + 80x2
subject to x1 + 2x2 ≤ 40
3x1 + x2 ≤ 60
x1, x2 ≥ 0
Using the simplex method, what is the optimal value for X2?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
53
Given the following linear programming problem:
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
What is the value of x2 in the final tableau?
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
What is the value of x2 in the final tableau?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
54
Given the following linear programming problem:
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
What is the optimal value of this objective function?
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
What is the optimal value of this objective function?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the following problem using the simplex method.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
56
Given the following linear programming problem:
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
How many iterations did we have to perform before reaching the final tableau?
maximize 4x1 + 3x2
subject to 4x1 + 3x2 ≤ 23
5x1 - x2 ≤ 5
x1, x2 ≥ 0
How many iterations did we have to perform before reaching the final tableau?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
57
Given the following linear programming problem:
Using the simplex method, what is the value for S2 in the optimal tableau?
Using the simplex method, what is the value for S2 in the optimal tableau?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
58
Given the following linear programming problem:
What is the (Ci- Zi) value for S2 at the initial solution?
What is the (Ci- Zi) value for S2 at the initial solution?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the following problem using the simplex method.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
60
Given the following linear programming problem:
What is the (Cj - Zj) value for S1 at the initial solution?
What is the (Cj - Zj) value for S1 at the initial solution?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
61
Slack variables are added to ________ constraints and represent unused resources.
A) ≤
B) <
C) ≥
D) >
E) =
A) ≤
B) <
C) ≥
D) >
E) =

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
62
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-To what value can the profit on red nail polish drop before the solution would change?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-To what value can the profit on red nail polish drop before the solution would change?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
63
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-By how much will the second marketing restriction be exceeded?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-By how much will the second marketing restriction be exceeded?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
64
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-By how much can the amount of space decrease before there is a change in the profit?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-By how much can the amount of space decrease before there is a change in the profit?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
65
The basic feasible solution in the initial simplex tableau is the origin where all decision variables equal:
A) 0
B) 1
C) -1
D) 1 or -1
A) 0
B) 1
C) -1
D) 1 or -1

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
66
At the initial basic feasible solution at the origin, only slack variables have a value greater than:
A) 0
B) 1
C) -1
D) 1 or -1
A) 0
B) 1
C) -1
D) 1 or -1

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the following linear programming problem and the corresponding final tableau.
MAX Z = 3x1 + 5x2
s.t. x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≥ 18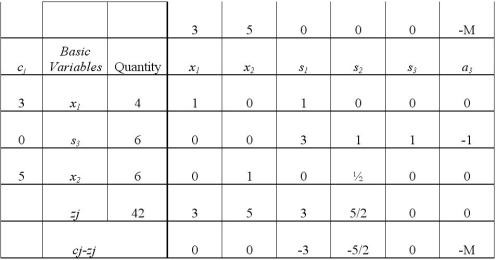
What is the sensitivity range for the first constraint?
MAX Z = 3x1 + 5x2
s.t. x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≥ 18

What is the sensitivity range for the first constraint?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
68
You are offered the chance to obtain more space. The offer is for 15 units and the total price is 1500. What should you do?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
69
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-By how much can the profit on green nail polish increase before the solution would change?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-By how much can the profit on green nail polish increase before the solution would change?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the following linear programming problem and the corresponding final tableau.
MAX Z = 3x1 + 5x2
s.t. x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≥ 18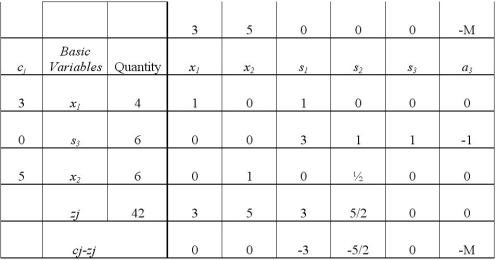
What is the shadow price for each constraint?
MAX Z = 3x1 + 5x2
s.t. x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≥ 18

What is the shadow price for each constraint?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
71
The ________ step in solving a linear programming model manually with the simplex method is to convert the model into standard form.
A) first
B) second
C) last
D) only
A) first
B) second
C) last
D) only

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
72
Row operations are used to solve simultaneous equations where equations are ________ by constants and added to or subtracted from each other.
A) converted
B) restrained
C) divided
D) multiplied
A) converted
B) restrained
C) divided
D) multiplied

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
73
The simplex method is a general mathematical solution technique for solving ________ programming problems.
A) integer
B) non-linear
C) linear
D) A, B, and C
A) integer
B) non-linear
C) linear
D) A, B, and C

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
74
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-What is the profit?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-What is the profit?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
75
At the initial basic feasible solution at the origin, only ________ variables have a value greater than zero.
A) linear
B) slack
C) non-linear
D) integer
A) linear
B) slack
C) non-linear
D) integer

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
76
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-How much time will be used?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-How much time will be used?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
77
The simplex method ________ be used to solve quadratic programming problems.
A) can
B) cannot
C) may
D) should
A) can
B) cannot
C) may
D) should

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
78
Write the dual form of the following linear program.
MAX Z = 3x1 + 5x2
s.t. x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≥ 18
MAX Z = 3x1 + 5x2
s.t. x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≥ 18

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
79
The linear programming problem whose output follows determines how many red nail polishes, blue nail polishes, green nail polishes, and pink nail polishes a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Constraints 3 and 4 are marketing restrictions.
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-How much space will be left unused?
MAX 100x1 + 120x2 + 150x3 + 125x4
Subject to 1. x1 + 2x2 + 2x3 + 2x4 ? 108
2. 3x1 + 5x2 + x4 ? 120
3. x1 + x3 ? 25
4. x2 + x3 + x4 > 50
x1, x2, x3, x4 ? 0
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-How much space will be left unused?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the following linear programming problem:
Use the two tables below to create the initial tableau and perform 1 pivot.
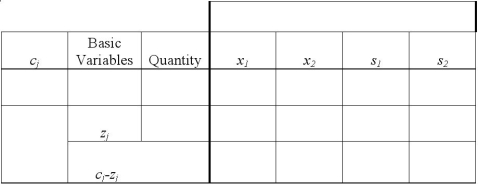
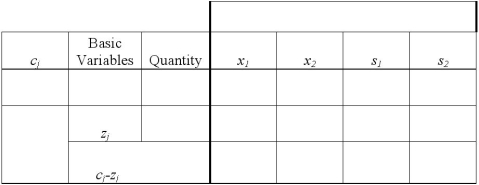
Use the two tables below to create the initial tableau and perform 1 pivot.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck


