Exam 17: the Simplex Solution Method
Exam 1: Management Science121 Questions
Exam 2: Linear Programming: Model Formulation and Graphical Solution122 Questions
Exam 3: Linear Programming: Computer Solution and Sensitivity Analysis95 Questions
Exam 4: Linear Programming: Modeling Examples90 Questions
Exam 5: Integer Programming107 Questions
Exam 6: Transportation, Transshipment, and Assignment Problems98 Questions
Exam 7: Network Flow Models104 Questions
Exam 8: Project Management116 Questions
Exam 9: Multicriteria Decision Making103 Questions
Exam 10: Nonlinear Programming72 Questions
Exam 11: Probability and Statistics152 Questions
Exam 12: Decision Analysis122 Questions
Exam 13: Queuing Analysis123 Questions
Exam 14: Simulation100 Questions
Exam 15: Forecasting133 Questions
Exam 16: Inventory Management157 Questions
Exam 17: the Simplex Solution Method90 Questions
Exam 18: Transportation and Assignment Solution Methods86 Questions
Exam 19: Integer Programming: the Branch and Bound Method63 Questions
Exam 20: Nonlinear Programming: Solution Techniques55 Questions
Exam 21: Game Theory64 Questions
Exam 22: Markov Analysis64 Questions
Select questions type
The simplex method is a general mathematical solution technique for solving linear programming problems.
Free
(True/False)
4.8/5  (37)
(37)
Correct Answer:
True
The simplex method is a general mathematical solution technique for solving ________ programming problems.
Free
(Multiple Choice)
4.7/5  (36)
(36)
Correct Answer:
C
Consider the following linear programming problem and the corresponding final tableau.
MAX Z=3+5 s.t. \leq4 2\leq12 3+2\geq18
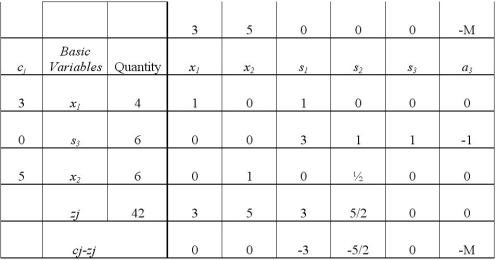 What is the shadow price for each constraint?
What is the shadow price for each constraint?
Free
(Essay)
4.9/5  (31)
(31)
Correct Answer:
constraint 1, 3; constraint 2, 2.5; constraint 3, 0
If the primal problem has three constraints, then the corresponding dual problem will have three ________.
(Short Answer)
4.8/5  (31)
(31)
Consider the following linear programming problem:
MAX =10+30 s.t. 4+6\leq12 8+4\leq16
Use the two tables below to create the initial tableau and perform 1 pivot.
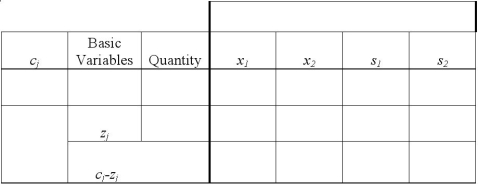
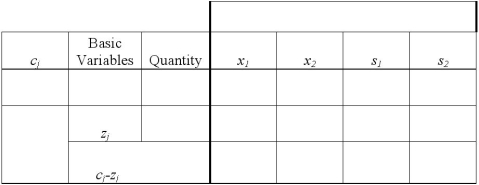
(Essay)
4.9/5  (32)
(32)
Slack variables are added to constraints and represent unused resources.
(True/False)
4.9/5  (30)
(30)
Write the dual form of the following linear program.
MAX =3+5 s.t. \leq4 2\leq12 3+2\geq18
(Essay)
4.8/5  (40)
(40)
Artificial variables are added to constraints and represent unused resources.
(True/False)
4.9/5  (38)
(38)
In solving a linear programming problem with simplex method, the number of basic variables is the same as the number of constraints in the original problem
(True/False)
4.7/5  (43)
(43)
The ________ step in solving a linear programming model manually with the simplex method is to convert the model into standard form.
(Multiple Choice)
4.7/5  (37)
(37)
Given the following linear programming problem:
maximize =\ 100+80 subject to +2\leq40 3+\leq60 ,\geq0
Using the simplex method, what is the optimal value for the objective function?
(Short Answer)
4.8/5  (41)
(41)
The leaving variable is determined by dividing the quantity values by the pivot column values and selecting the
(Multiple Choice)
4.7/5  (38)
(38)
The simplex method cannot be used to solve quadratic programming problems.
(True/False)
4.8/5  (41)
(41)
Given the following linear programming problem:
maximize 4+3 subject to 4+3\leq23 5-\leq5 ,\geq0
What is the (Ci- Zi) value for S2 at the initial solution?
(Short Answer)
4.9/5  (30)
(30)
________ in linear programming is when a basic variable takes on a value of zero (i.e., a zero in the right-hand side of the constraints of the tableau).
(Short Answer)
4.8/5  (36)
(36)
When solving a linear programming problem, a decision variable that leaves the basis in one iteration of the simplex method can return to the basis on a later iteration.
(True/False)
4.9/5  (42)
(42)
Row operations are used to solve simultaneous equations where equations are multiplied by constants and added or subtracted from each other.
(True/False)
4.7/5  (39)
(39)
Solve the following problem using the simplex method.
Minimize =2+6 Subject to: 2+4\leq12 3+2\geq9 ,\geq0
(Short Answer)
4.9/5  (38)
(38)
Given the following linear programming problem:
maximize 4+3 subject to 4+3\leq23 5-\leq5 ,\geq0
What is the value of x2 in the final tableau?
(Short Answer)
4.9/5  (27)
(27)
Showing 1 - 20 of 90
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)