Deck 23: Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/98
Play
Full screen (f)
Deck 23: Linear Programming
1
One requirement of a linear programming problem is that the objective function must be expressed as a linear equation or inequality.
True
2
A linear programming problem contains a restriction that reads "the quantity of Q must be no larger than the sum of R,S,and T." Formulate this as a linear programming constraint.
A)Q + R + S + T ≤ 4
B)Q ≥ R + S + T
C)Q - R - S - T ≤ 0
D)Q / (R + S + T)≤ 0
E)Q ≤ R + Q ≤ S + Q ≤ T
A)Q + R + S + T ≤ 4
B)Q ≥ R + S + T
C)Q - R - S - T ≤ 0
D)Q / (R + S + T)≤ 0
E)Q ≤ R + Q ≤ S + Q ≤ T
C
3
A common form of the product-mix linear programming problem seeks to find that combination of products and the quantity of each that maximizes profit in the presence of limited resources.
True
4
Linear programming helps operations managers make decisions necessary to make effective use of resources such as machinery,labor,money,time,and raw materials.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following represents a valid constraint in linear programming?
A)2X ≥ 7XY
B)(2X)(7Y)≥ 500
C)2X + 7Y ≥100
D)2X2 + 7Y ≥ 50
E)All of the above are valid linear programming constraints.
A)2X ≥ 7XY
B)(2X)(7Y)≥ 500
C)2X + 7Y ≥100
D)2X2 + 7Y ≥ 50
E)All of the above are valid linear programming constraints.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
6
Identify three examples of resources that are typically constrained in a linear programming problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
7
In a linear programming formulation,a statement such as "maximize contribution" becomes a(n):
A)constraint.
B)slack variable.
C)objective function.
D)violation of linearity.
E)decision variable.
A)constraint.
B)slack variable.
C)objective function.
D)violation of linearity.
E)decision variable.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
8
Linear programming is an appropriate problem-solving technique for decisions that have no alternative courses of action.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
9
In linear programming,a statement such as "maximize contribution" becomes an objective function when the problem is formulated.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
10
What is linear programming?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
11
________ are restrictions that limit the degree to which a manager can pursue an objective.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
12
A linear programming problem contains a restriction that reads "the quantity of X must be at least three times as large as the quantity of Y." Which of the following inequalities is the proper formulation of this constraint?
A)3X ≥ Y
B)X ≤ 3Y
C)X + Y ≥ 3
D)X - 3Y ≥ 0
E)3X ≤ Y
A)3X ≥ Y
B)X ≤ 3Y
C)X + Y ≥ 3
D)X - 3Y ≥ 0
E)3X ≤ Y

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
13
________ is a mathematical technique designed to help operations managers plan and make decisions necessary to allocate resources.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
14
A linear programming problem contains a restriction that reads "the quantity of S must be no less than one-fourth as large as T and U combined." Formulate this as a linear programming constraint.
A)S / (T + U)≥ 4
B)S - .25T - .25U ≥ 0
C)4S ≤ T + U
D)S ≥ 4T / 4U
E)S ≥ .25T + S ≥ .25U
A)S / (T + U)≥ 4
B)S - .25T - .25U ≥ 0
C)4S ≤ T + U
D)S ≥ 4T / 4U
E)S ≥ .25T + S ≥ .25U

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
15
The ________ is a mathematical expression in linear programming that maximizes or minimizes some quantity.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is not a requirement of a linear programming problem?
A)an objective function,expressed in linear terms
B)constraints,expressed as linear equations or inequalities
C)an objective function to be maximized or minimized
D)alternative courses of action
E)one constraint or resource limit for each decision variable
A)an objective function,expressed in linear terms
B)constraints,expressed as linear equations or inequalities
C)an objective function to be maximized or minimized
D)alternative courses of action
E)one constraint or resource limit for each decision variable

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
17
What are the requirements of all linear programming problems?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
18
A firm makes two products,Y and Z.Each unit of Y costs $10 and sells for $40.Each unit of Z costs $5 and sells for $25.If the firm's goal were to maximize profit,what would be the appropriate objective function?
A)Maximize profit = $40Y = $25Z
B)Maximize profit = $40Y + $25Z
C)Maximize profit = $30Y + $20Z
D)Maximize profit = 0.25Y + 0.20Z
E)Maximize profit = $50(Y + Z)
A)Maximize profit = $40Y = $25Z
B)Maximize profit = $40Y + $25Z
C)Maximize profit = $30Y + $20Z
D)Maximize profit = 0.25Y + 0.20Z
E)Maximize profit = $50(Y + Z)

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
19
In which of the following has LP been applied successfully?
A)minimizing distance traveled by school buses carrying children
B)minimizing 911 response time for police patrols
C)minimizing labor costs for bank tellers while maintaining service levels
D)determining the distribution system for multiple warehouses to multiple destinations
E)all of the above
A)minimizing distance traveled by school buses carrying children
B)minimizing 911 response time for police patrols
C)minimizing labor costs for bank tellers while maintaining service levels
D)determining the distribution system for multiple warehouses to multiple destinations
E)all of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
20
The requirements of linear programming problems include an objective function,the presence of constraints,objective and constraints expressed in linear equalities or inequalities,and ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
21
In terms of linear programming,the fact that the solution is infeasible implies that the "profit" can increase without limit.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following combinations of constraints has no feasible region?
A)X + Y ≥ 15 and X - Y ≤ 10
B)X + Y ≥ 5 and X ≥ 10
C)X ≥ 10 and Y ≥ 20
D)X + Y ≥ 100 and X + Y ≤ 50
E)X ≤ -5
A)X + Y ≥ 15 and X - Y ≤ 10
B)X + Y ≥ 5 and X ≥ 10
C)X ≥ 10 and Y ≥ 20
D)X + Y ≥ 100 and X + Y ≤ 50
E)X ≤ -5

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
23
A linear programming problem contains a restriction that reads "the quantity of Q must be at least as large as the sum of R,S,and T." Formulate this as a linear programming constraint.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
24
Using the iso-profit line solution method to solve a maximization problem requires that we:
A)find the value of the objective function at the origin.
B)move the iso-profit line away from the origin until it barely touches some part of the feasible region.
C)move the iso-cost line to the lowest level that still touches some part of the feasible region.
D)test the objective function value of every corner point in the feasible region.
E)none of the above
A)find the value of the objective function at the origin.
B)move the iso-profit line away from the origin until it barely touches some part of the feasible region.
C)move the iso-cost line to the lowest level that still touches some part of the feasible region.
D)test the objective function value of every corner point in the feasible region.
E)none of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
25
The feasible region in the diagram below is consistent with which one of the following constraints? 
A)8X1 + 4X2 ≤ 160
B)8X1 + 4X2 ≥ 160
C)4X1 + 8X2 ≤ 160
D)8X1 - 4X2 ≤ 160
E)4X1 - 8X2 ≤ 160

A)8X1 + 4X2 ≤ 160
B)8X1 + 4X2 ≥ 160
C)4X1 + 8X2 ≤ 160
D)8X1 - 4X2 ≤ 160
E)4X1 - 8X2 ≤ 160

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
26
A linear programming problem contains a restriction that reads "the quantity of X must be at least twice as large as the quantity of Y." Formulate this as a linear programming constraint.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
27
What is the region that satisfies all of the constraints in linear programming called?
A)area of optimal solutions
B)area of feasible solutions
C)profit maximization space
D)region of optimality
E)region of non-negativity
A)area of optimal solutions
B)area of feasible solutions
C)profit maximization space
D)region of optimality
E)region of non-negativity

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
28
In linear programming,if there are three constraints,each representing a resource that can be used up,the optimal solution must use up all of each of the three resources.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
29
An iso-profit line:
A)can be used to help solve a profit maximizing linear programming problem.
B)is parallel to all other iso-profit lines in the same problem.
C)is a line with the same profit at all points.
D)all of the above
E)none of the above
A)can be used to help solve a profit maximizing linear programming problem.
B)is parallel to all other iso-profit lines in the same problem.
C)is a line with the same profit at all points.
D)all of the above
E)none of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
30
Solving a linear programming problem with the iso-profit line solution method requires that we move the iso-profit line to each corner of the feasible region until the optimum is identified.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
31
For the constraints given below,which point is in the feasible region of this maximization problem? (1)14x + 6y ≤ 42 (2)x - y ≤ 3 (3)x,y ≥ 0
A)x = 2,y = 1
B)x = 1,y = 5
C)x = -1,y = 1
D)x = 4,y = 4
E)x = 2,y = 8
A)x = 2,y = 1
B)x = 1,y = 5
C)x = -1,y = 1
D)x = 4,y = 4
E)x = 2,y = 8

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
32
For the following constraints,which point is in the feasible region of this minimization problem? (1)14x + 6y ≥ 42 (2)x - y ≥ 3
A)x = -1,y = 1
B)x = 0,y = 4
C)x = 2,y = 1
D)x = 5,y = 1
E)x = 2,y = 0
A)x = -1,y = 1
B)x = 0,y = 4
C)x = 2,y = 1
D)x = 5,y = 1
E)x = 2,y = 0

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
33
The feasible region in the diagram below is consistent with which one of the following constraints? 
A)8X1 + 4X2 ≥ 160
B)4X1 + 8X2 ≤ 160
C)8X1 - 4X2 ≤ 160
D)8X1 + 4X2 ≤ 160
E)4X1 - 8X2 ≤ 160

A)8X1 + 4X2 ≥ 160
B)4X1 + 8X2 ≤ 160
C)8X1 - 4X2 ≤ 160
D)8X1 + 4X2 ≤ 160
E)4X1 - 8X2 ≤ 160

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
34
For a linear programming problem with the constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100,two of its corner points are (0,0)and (0,25).

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
35
A linear programming problem contains a restriction that reads "the quantity of S must be no more than one-fourth as large as T and U combined." Formulate this as a linear programming constraint.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following sets of constraints results in an unbounded maximization problem?
A)X + Y ≥ 100 and X + Y ≤ 50
B)X + Y ≥ 15 and X - Y ≤ 10
C)X + Y ≤ 10 and X ≥ 5
D)X ≤ 10 and Y ≤ 20
E)All of the above have a bounded maximum.
A)X + Y ≥ 100 and X + Y ≤ 50
B)X + Y ≥ 15 and X - Y ≤ 10
C)X + Y ≤ 10 and X ≥ 5
D)X ≤ 10 and Y ≤ 20
E)All of the above have a bounded maximum.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
37
In the graphical solution to a linear program,the region that satisfies the constraint 4X + 15Z ≥ 1000 includes the origin of the graph.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
38
The corner-point solution method requires:
A)identifying the corner of the feasible region that has the sharpest angle.
B)moving the iso-profit line to the highest level that still touches some part of the feasible region.
C)moving the iso-profit line to the lowest level that still touches some part of the feasible region.
D)finding the coordinates at each corner of the feasible solution space.
E)none of the above
A)identifying the corner of the feasible region that has the sharpest angle.
B)moving the iso-profit line to the highest level that still touches some part of the feasible region.
C)moving the iso-profit line to the lowest level that still touches some part of the feasible region.
D)finding the coordinates at each corner of the feasible solution space.
E)none of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
39
The region that satisfies all of the constraints in linear programming is called the region of optimality.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
40
The optimal solution to a linear programming problem lies within the feasible region.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
41
The objective of a linear programming problem is to maximize 1.50A + 1.50B,subject to 3A + 2B ≤ 600,2A + 4B ≤ 600,1A + 3B ≤ 420,and A,B ≥ 0.
a.Plot the constraints on the grid below
c.Identify the feasible region and its corner points.Show your work.
d.What is the optimal product mix for this problem?
a.Plot the constraints on the grid below
c.Identify the feasible region and its corner points.Show your work.
d.What is the optimal product mix for this problem?


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
42
What combination of x and y will yield the optimum for this problem? Minimize $3x + $15y,subject to (1)2x + 4y ≤ 12 and (2)5x + 2y ≤ 10 and (3)x,y ≥ 0.
A)x = 2,y = 0
B)x = 0,y = 3
C)x = 0,y = 0
D)x = 1,y = 5
E)x = 0,y = 5
A)x = 2,y = 0
B)x = 0,y = 3
C)x = 0,y = 0
D)x = 1,y = 5
E)x = 0,y = 5

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
43
A linear programming problem has three constraints,plus nonnegativity constraints on X and Y.The constraints are: 2X + 10Y ≤ 100;4X + 6Y ≤ 120;6X + 3Y ≤ 90. What is the largest quantity of X that can be made without violating any of these constraints?
A)50
B)30
C)20
D)15
E)10
A)50
B)30
C)20
D)15
E)10

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
44
Two methods of solving linear programming problems by hand include the corner-point method and the ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the following constraints from a two-variable linear program: X ≥ 1;Y ≥ 1;X + Y ≤ 9. If these are the only constraints,which of the following points (X,Y)CANNOT be the optimal solution?
A)(1,1)
B)(1,8)
C)(8,1)
D)(4,4)
E)The question cannot be answered without knowing the objective function.
A)(1,1)
B)(1,8)
C)(8,1)
D)(4,4)
E)The question cannot be answered without knowing the objective function.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose that the feasible region of a maximization LP problem has corners of (0,0), (10,0), (5,5),and (0,7).If profit is given to be $X + $2Y what is the maximum profit the company can earn?
A)$0
B)$10
C)$15
D)$14
E)$24
A)$0
B)$10
C)$15
D)$14
E)$24

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
47
What combination of x and y will yield the optimum for this problem? Maximize $3x + $15y,subject to (1)2x + 4y ≤ 12 and (2)5x + 2y ≤ 10 and (3)x,y ≥ 0.
A)x = 2,y = 0
B)x = 0,y = 3
C)x = 0,y = 0
D)x = 1,y = 5
E)x = 0,y = 5
A)x = 2,y = 0
B)x = 0,y = 3
C)x = 0,y = 0
D)x = 1,y = 5
E)x = 0,y = 5

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
48
A linear programming problem has two constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100,plus nonnegativity constraints on X and Y.Which of the following statements about its feasible region is TRUE?
A)There are four corner points including (50,0)and (0,12.5).
B)The two corner points are (0,0)and (50,12.5).
C)The graphical origin (0,0)is not in the feasible region.
D)The feasible region includes all points that satisfy one constraint,the other,or both.
E)The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized.
A)There are four corner points including (50,0)and (0,12.5).
B)The two corner points are (0,0)and (50,12.5).
C)The graphical origin (0,0)is not in the feasible region.
D)The feasible region includes all points that satisfy one constraint,the other,or both.
E)The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
49
What is the feasible region in a linear programming problem?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose that the feasible region of a maximization LP problem has corners of (0,0), (5,0),and (0,5).How many possible combinations of X and Y will yield the maximum profit if profit is given to be 5X + 5Y?
A)0
B)1
C)2
D)5
E)Infinite
A)0
B)1
C)2
D)5
E)Infinite

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
51
A linear programming problem has two constraints 2X + 4Y ≥ 100 and 1X + 8Y ≤ 100,plus nonnegativity constraints on X and Y.Which of the following statements about its feasible region is TRUE?
A)There are four corner points including (50,0)and (0,12.5).
B)The two corner points are (0,0)and (50,12.5).
C)The graphical origin (0,0)is in the feasible region.
D)The feasible region is triangular in shape,bounded by (50,0), (33.3333,8.3333),and (100,0).
E)The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized.
A)There are four corner points including (50,0)and (0,12.5).
B)The two corner points are (0,0)and (50,12.5).
C)The graphical origin (0,0)is in the feasible region.
D)The feasible region is triangular in shape,bounded by (50,0), (33.3333,8.3333),and (100,0).
E)The feasible region cannot be determined without knowing whether the problem is to be minimized or maximized.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
52
A manager must decide on the mix of products to produce for the coming week.Product A requires three minutes per unit for molding,two minutes per unit for painting,and one minute for packing.Product B requires two minutes per unit for molding,four minutes for painting,and three minutes per unit for packing.There will be 600 minutes available for molding,600 minutes for painting,and 420 minutes for packing.Both products have contributions of $1.50 per unit.
a.Algebraically state the objective and constraints of this problem.
b.Plot the constraints on the grid below and identify the feasible region.
a.Algebraically state the objective and constraints of this problem.
b.Plot the constraints on the grid below and identify the feasible region.


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose that an iso-profit line is given to be X + Y = 10.Which of the following represents another iso-profit line for the same scenario?
A)X + Y = 15
B)X - Y = 10
C)Y - X = 10
D)2X + Y = 10
E)none of the above
A)X + Y = 15
B)X - Y = 10
C)Y - X = 10
D)2X + Y = 10
E)none of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
54
What are corner points? What is their relevance to solving linear programming problems?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the following correctly describes all iso-profit lines for an LP maximization problem?
A)They all pass through the origin
B)They are all parallel.
C)They all pass through the point of maximum profit.
D)Each line passes through at least 2 corners.
E)all of the above
A)They all pass through the origin
B)They are all parallel.
C)They all pass through the point of maximum profit.
D)Each line passes through at least 2 corners.
E)all of the above

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
56
A maximizing linear programming problem has two constraints: 2X + 4Y ≤ 100 and 3X + 10Y ≤ 210,in addition to constraints stating that both X and Y must be nonnegative.What are the corner points of the feasible region of this problem?
A)(0,0), (50,0), (0,21),and (20,15)
B)(0,0), (70,0), (25,0),and (15,20)
C)(20,15)
D)(0,0), (0,100),and (210,0)
E)(0,0), (0,25), (50,0), (0,21),and (70,0)
A)(0,0), (50,0), (0,21),and (20,15)
B)(0,0), (70,0), (25,0),and (15,20)
C)(20,15)
D)(0,0), (0,100),and (210,0)
E)(0,0), (0,25), (50,0), (0,21),and (70,0)

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
57
Explain how to use the iso-profit line in a graphical solution to maximization problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
58
A linear programming problem has three constraints,plus nonnegativity constraints on X and Y.The constraints are: 2X + 10Y ≤ 100;4X + 6Y ≤ 120;6X + 3Y ≥ 90. What is the largest quantity of X that can be made without violating any of these constraints?
A)50
B)30
C)20
D)15
E)10
A)50
B)30
C)20
D)15
E)10

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
59
What combination of a and b will yield the optimum for this problem? Maximize $6a + $15b,subject to (1)4a + 2b ≤ 12 and (2)5a + 2b ≤ 20 and (3)x,y ≥ 0.
A)a = 0,b = 0
B)a = 3,b = 3
C)a = 0,b = 6
D)a = 6,b = 0
E)a = 0,b = 10
A)a = 0,b = 0
B)a = 3,b = 3
C)a = 0,b = 6
D)a = 6,b = 0
E)a = 0,b = 10

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
60
The ________ is the set of all feasible combinations of the decision variables.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
61
A financial advisor is about to build an investment portfolio for a client who has $100,000 to invest.The four investments available are A,B,C,and D.Investment A will earn 4 percent and has a risk of two "points" per $1,000 invested.B earns 6 percent with 3 risk points;C earns 9 percent with 7 risk points;and D earns 11 percent with a risk of 8.The client has put the following conditions on the investments: A is to be no more than one-half of the total invested.A cannot be less than 20 percent of the total investment.D cannot be less than C.Total risk points must be at or below 1,000.
Let A be the amount invested in investment A,and define B,C,and D similarly.
Formulate the linear programming model.
Let A be the amount invested in investment A,and define B,C,and D similarly.
Formulate the linear programming model.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
62
What is sensitivity analysis?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
63
The Queen City Nursery manufactures bags of potting soil from compost and topsoil.Each cubic foot of compost costs 12 cents and contains 4 pounds of sand,3 pounds of clay,and 5 pounds of humus.Each cubic foot of topsoil costs 20 cents and contains 3 pounds of sand,6 pounds of clay,and 12 pounds of humus.Each bag of potting soil must contain at least 12 pounds of sand,at least 12 pounds of clay,and at least 10 pounds of humus.Formulate the problem as a linear program.Plot the constraints and identify the feasible region.Graphically or with corner points find the best combination of compost and topsoil that meets the stated conditions at the lowest cost per bag.Identify the lowest cost possible.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
64
A craftsman builds two kinds of birdhouses,one for wrens (X1),and one for bluebirds (X2).Each wren birdhouse takes four hours of labor and four units of lumber.Each bluebird house requires two hours of labor and twelve units of lumber.The craftsman has available 60 hours of labor and 120 units of lumber.Wren houses profit $6 each and bluebird houses profit $15 each.
Use the software output that follows to interpret the problem solution.Include a statement of the solution quantities (how many of which product),a statement of the maximum profit achieved by your product mix,and a statement of "resources unused" and "shadow prices."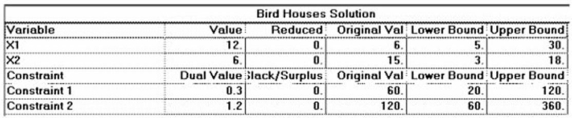
Use the software output that follows to interpret the problem solution.Include a statement of the solution quantities (how many of which product),a statement of the maximum profit achieved by your product mix,and a statement of "resources unused" and "shadow prices."


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
65
A manager must decide on the mix of products to produce for the coming week.Product A requires three minutes per unit for molding,two minutes per unit for painting,and one minute for packing.Product B requires two minutes per unit for molding,four minutes for painting,and three minutes per unit for packing.There will be 600 minutes available for molding,600 minutes for painting,and 420 minutes for packing.Both products have contributions of $1.50 per unit.Answer the following questions;base your work on the solution panel provided.
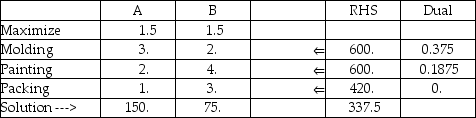 a.What combination of A and B will maximize contribution?
a.What combination of A and B will maximize contribution?
b.What is the maximum possible contribution?
c.Are any resources not fully used up? Explain.
 a.What combination of A and B will maximize contribution?
a.What combination of A and B will maximize contribution?b.What is the maximum possible contribution?
c.Are any resources not fully used up? Explain.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
66
________ is an analysis that projects how much a solution might change if there were changes in the variables or input data.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
67
In sensitivity analysis,a zero shadow price (or dual value)for a resource ordinarily means that the resource has not been used up.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
68
A difference between minimization and maximization problems is that:
A)minimization problems cannot be solved with the corner-point method.
B)maximization problems often have unbounded regions.
C)minimization problems often have unbounded regions.
D)minimization problems cannot have shadow prices.
E)minimization problems are more difficult to solve than maximization problems.
A)minimization problems cannot be solved with the corner-point method.
B)maximization problems often have unbounded regions.
C)minimization problems often have unbounded regions.
D)minimization problems cannot have shadow prices.
E)minimization problems are more difficult to solve than maximization problems.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
69
A shadow price (or dual value)reflects which of the following in a maximization problem?
A)the marginal gain in the objective realized by subtracting one unit of a resource
B)the market price that must be paid to obtain additional resources
C)the increase in profit that would accompany one added unit of a scarce resource
D)the reduction in cost that would accompany a one unit decrease in the resource
E)the profit contribution necessary for that item to be included in the optimal solution
A)the marginal gain in the objective realized by subtracting one unit of a resource
B)the market price that must be paid to obtain additional resources
C)the increase in profit that would accompany one added unit of a scarce resource
D)the reduction in cost that would accompany a one unit decrease in the resource
E)the profit contribution necessary for that item to be included in the optimal solution

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
70
Rienzi Farms grows sugar cane and soybeans on its 500 acres of land.An acre of soybeans brings a $1000 contribution to overhead and profit;an acre of sugar cane has a contribution of $2000.Because of a government program no more than 200 acres may be planted in soybeans.During the planting season 1200 hours of planting time will be available.Each acre of soybeans requires 2 hours,while each acre of sugar cane requires 5 hours.The company seeks maximum contribution (profit)from its planting decision.
a.Formulate the problem as a linear program.
b.Solve using the corner-point method.
a.Formulate the problem as a linear program.
b.Solve using the corner-point method.


Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
71
A synonym for shadow price is ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
72
The graphical method of solving linear programs can handle only maximization problems.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
73
Suppose that a constraint is given by X + Y ≤ 10.If another constraint is given to be 3X + 2Y ≥ 15,and if X and Y are restricted to be nonnegative,determine the corners of the feasible solution.If the profit from X is 5 and the profit from Y is 10,determine the combination of X and Y that will yield maximum profit.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
74
What is the usefulness of a shadow price (or dual value)?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
75
The diet problem is known in agricultural applications as the:
A)fertilizer problem.
B)feed-mix problem.
C)crop-rotation problem.
D)egg-choice problem.
E)genetic-transformation problem.
A)fertilizer problem.
B)feed-mix problem.
C)crop-rotation problem.
D)egg-choice problem.
E)genetic-transformation problem.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
76
Suppose that the shadow price for assembly time is $5/hour.The allowable increase for the assembly time constraint is 40 hours,and the allowable decrease is 30 hours.If all assembly hours were used under the initial LP solution and workers normally make $4/hour but can work overtime for $6/hour,what should management do?
A)do not change available hours for assembly time
B)decrease available hours for assembly time by 30 hours
C)increase available hours for assembly time by 40 hours
D)decrease available hours for assembly time by 5 hours
E)increase available hours for assembly time by 5 hours
A)do not change available hours for assembly time
B)decrease available hours for assembly time by 30 hours
C)increase available hours for assembly time by 40 hours
D)decrease available hours for assembly time by 5 hours
E)increase available hours for assembly time by 5 hours

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
77
Suppose that a constraint for assembly time has a shadow price of $50/hour for 15 hours in either direction and that all available assembly time is currently used (would require overtime to do more).If the salary of workers is $30 and they receive 50% extra pay for overtime what should management do?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
78
Sensitivity analysis can be applied to linear programming solutions by either (1)trial and error or (2)the analytic postoptimality method.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
79
In linear programming,statements such as "the blend must consist of at least 10% of ingredient A,at least 30% of ingredient B,and no more than 50% of ingredient C" can be made into valid constraints even though the percentages do not add up to 100 percent.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
80
Two methods of conducting sensitivity analysis on solved linear programming problems are ________ and ________.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck


