Exam 23: Linear Programming
Exam 1: Operations and Productivity129 Questions
Exam 2: Operations Strategy in a Global Environment120 Questions
Exam 3: Project Management124 Questions
Exam 4: Forecasting141 Questions
Exam 5: Design of Goods and Services121 Questions
Exam 6: Managing Quality125 Questions
Exam 7: Process Strategy113 Questions
Exam 8: Location Strategies121 Questions
Exam 9: Layout Strategies146 Questions
Exam 10: Human Resources,job Design,and Work Measurement159 Questions
Exam 11: Supply Chain Management145 Questions
Exam 12: Inventory Management165 Questions
Exam 13: Aggregate Planning and Sop116 Questions
Exam 14: Material Requirements Planning Mrpand ERP113 Questions
Exam 15: Short-Term Scheduling116 Questions
Exam 16: Lean Operations116 Questions
Exam 17: Maintenance and Reliability114 Questions
Exam 18: Sustainability in the Supply Chain84 Questions
Exam 19: Statistical Process Control144 Questions
Exam 20: Capacity and Constraint Management101 Questions
Exam 21: Supply Chain Management Analytics67 Questions
Exam 22: Decision-Making Tools100 Questions
Exam 23: Linear Programming98 Questions
Exam 24: Transportation Models89 Questions
Exam 25: Waiting-Line Models119 Questions
Exam 26: Learning Curves110 Questions
Exam 27: Simulation75 Questions
Select questions type
The region that satisfies all of the constraints in linear programming is called the region of optimality.
Free
(True/False)
4.8/5  (33)
(33)
Correct Answer:
False
Explain how to use the iso-profit line in a graphical solution to maximization problem.
Free
(Essay)
4.7/5  (34)
(34)
Correct Answer:
The iso-profit line is moved up in a maximization problem until it no longer intersects with any constraint equation.The last point in the feasible region that the line touches is the optimal solution.
What are corner points? What is their relevance to solving linear programming problems?
Free
(Essay)
4.9/5  (28)
(28)
Correct Answer:
Corner points are the intersections of the constraints that form the feasible region.While all points in the feasible region are possible,an optimal solution will always be at a corner point.Therefore,one method of solving linear programming problems involves the identification and valuation of all corner points.
________ are restrictions that limit the degree to which a manager can pursue an objective.
(Essay)
4.9/5  (37)
(37)
If we wish to ensure that decision variable values in a linear program are integers rather than fractions,the generally accepted practice is to round the solutions to the nearest integer values.
(True/False)
4.9/5  (25)
(25)
Constraints are needed to solve linear programming problems by hand,but not by computer.
(True/False)
4.9/5  (37)
(37)
In linear programming,statements such as "the blend must consist of at least 10% of ingredient A,at least 30% of ingredient B,and no more than 50% of ingredient C" can be made into valid constraints even though the percentages do not add up to 100 percent.
(True/False)
5.0/5  (34)
(34)
The main disadvantage of introducing constraints into a linear program that enforce some or all of the decision variables to be either integer or binary is that:
(Multiple Choice)
4.8/5  (33)
(33)
Identify three examples of resources that are typically constrained in a linear programming problem.
(Essay)
4.8/5  (34)
(34)
Computer software provides a simple way to guarantee only integer solutions to linear programming problems.
(True/False)
4.9/5  (24)
(24)
A linear programming problem has two constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100,plus nonnegativity constraints on X and Y.Which of the following statements about its feasible region is TRUE?
(Multiple Choice)
4.8/5  (28)
(28)
Riker Co.is considering which of 4 different projects to undertake in order to maximize its net present value (NPV).Define Xi as a binary variable that equals 1 if project i is undertaken and 0 otherwise,for i = 1,2,3,4.The NPV and required capital (in millions)for each project are listed below.
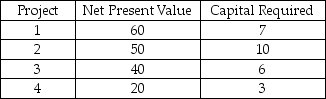 Which of the following represents the constraint(s)stating that project 1 must be undertaken and at least one of the other projects must be undertaken?
Which of the following represents the constraint(s)stating that project 1 must be undertaken and at least one of the other projects must be undertaken?
(Multiple Choice)
4.8/5  (46)
(46)
Riker Co.is considering which of 4 different projects to undertake in order to maximize its net present value (NPV).Define Xi as a binary variable that equals 1 if project i is undertaken and 0 otherwise,for i = 1,2,3,4.The NPV and required capital (in millions)for each project are listed below.
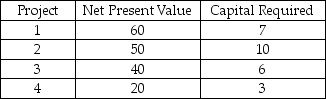 What is the proper objective function?
What is the proper objective function?
(Multiple Choice)
4.8/5  (36)
(36)
A linear programming problem contains a restriction that reads "the quantity of Q must be at least as large as the sum of R,S,and T." Formulate this as a linear programming constraint.
(Essay)
4.7/5  (41)
(41)
A manager must decide on the mix of products to produce for the coming week.Product A requires three minutes per unit for molding,two minutes per unit for painting,and one minute for packing.Product B requires two minutes per unit for molding,four minutes for painting,and three minutes per unit for packing.There will be 600 minutes available for molding,600 minutes for painting,and 420 minutes for packing.Both products have contributions of $1.50 per unit.Answer the following questions;base your work on the solution panel provided.
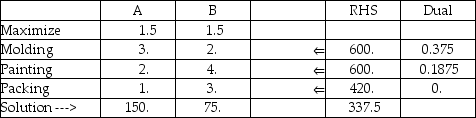 a.What combination of A and B will maximize contribution?
b.What is the maximum possible contribution?
c.Are any resources not fully used up? Explain.
a.What combination of A and B will maximize contribution?
b.What is the maximum possible contribution?
c.Are any resources not fully used up? Explain.
(Essay)
4.9/5  (37)
(37)
Capital Co.is considering 5 different projects.Define Xi as a binary variable that equals 1 if project i is undertaken and 0 otherwise,for i = 1,2,3,4,5.Which of the following represents the constraint(s)stating that projects 2,3,and 4 cannot all three be undertaken simultaneously?
(Multiple Choice)
4.9/5  (38)
(38)
A feedlot is trying to decide on the lowest cost mix that will still provide adequate nutrition for its cattle.Suppose that the numbers in the chart represent the number of grams of ingredient per 100 grams of feed and that the cost of Feed X is $5/100grams,Feed Y is $3/100 grams,and Feed X is $8/100 grams.Each cow will need 50 grams of A per day,20 grams of B,30 grams of C,and 10 grams of D.The feedlot can get no more than 200 grams per day per cow of any of the feed types.Formulate the problem as a linear program.
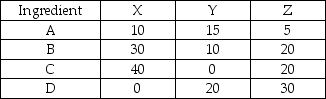
(Essay)
4.8/5  (34)
(34)
Showing 1 - 20 of 98
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)