Deck 12: Rotation of a Rigid Body
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/113
Play
Full screen (f)
Deck 12: Rotation of a Rigid Body
1
A tire is rolling along a road, without slipping, with a velocity v. A piece of tape is attached to the tire. When the tape is opposite the road (at the top of the tire), its velocity with respect to the road is
A) 2v.
B) v.
C) 1.5v.
D) zero.
E) The velocity depends on the radius of the tire.
A) 2v.
B) v.
C) 1.5v.
D) zero.
E) The velocity depends on the radius of the tire.
2v.
2
A heavy boy and a lightweight girl are balanced on a massless seesaw. If they both move forward so that they are one-half their original distance from the pivot point, what will happen to the seesaw? Assume that both people are small enough compared to the length of the seesaw to be thought of as point masses.
A) It is impossible to say without knowing the masses.
B) It is impossible to say without knowing the distances.
C) The side the boy is sitting on will tilt downward.
D) Nothing will happen; the seesaw will still be balanced.
E) The side the girl is sitting on will tilt downward.
A) It is impossible to say without knowing the masses.
B) It is impossible to say without knowing the distances.
C) The side the boy is sitting on will tilt downward.
D) Nothing will happen; the seesaw will still be balanced.
E) The side the girl is sitting on will tilt downward.
Nothing will happen; the seesaw will still be balanced.
3
When you ride a bicycle, in what direction is the angular velocity of the wheels?
A) to your left
B) to your right
C) forwards
D) backwards
E) up
A) to your left
B) to your right
C) forwards
D) backwards
E) up
to your left
4
There must be equal amounts of mass on both side of the center of mass of an object.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
5
A horizontal disk rotates about a vertical axis through its center. Point P is midway between the center and the rim of the disk, and point Q is on the rim. If the disk turns with constant angular velocity, which of the following statements about it are true? (There may be more than one correct choice.)
A) P and Q have the same linear acceleration.
B) Q is moving twice as fast as P.
C) The linear acceleration of Q is twice as great as the linear acceleration of P.
D) The linear acceleration of P is twice as great as the linear acceleration of Q.
E) The angular velocity of Q is twice as great as the angular velocity of P.
A) P and Q have the same linear acceleration.
B) Q is moving twice as fast as P.
C) The linear acceleration of Q is twice as great as the linear acceleration of P.
D) The linear acceleration of P is twice as great as the linear acceleration of Q.
E) The angular velocity of Q is twice as great as the angular velocity of P.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
6
A dumbbell-shaped object is composed by two equal masses, m, connected by a rod of negligible mass and length r. If I1 is the moment of inertia of this object with respect to an axis passing through the center of the rod and perpendicular to it and I2 is the moment of inertia with respect to an axis passing through one of the masses, it follows that
A) I1 = I2.
B) I1 > I2.
C) I2 > I1.
A) I1 = I2.
B) I1 > I2.
C) I2 > I1.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
7
As you are leaving a building, the door opens outward. If the hinges on the door are on your right, what is the direction of the angular velocity of the door as you open it?
A) up
B) down
C) to your left
D) to your right
E) forwards
A) up
B) down
C) to your left
D) to your right
E) forwards

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
8
If two vectors point in opposite directions, their cross product must be zero.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
9
If the torque on an object adds up to zero
A) the forces on it also add up to zero.
B) the object is at rest.
C) the object cannot be turning.
D) the object could be accelerating linearly but it could not be turning.
E) the object could be both turning and accelerating linearly.
A) the forces on it also add up to zero.
B) the object is at rest.
C) the object cannot be turning.
D) the object could be accelerating linearly but it could not be turning.
E) the object could be both turning and accelerating linearly.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
10
A metal bar is hanging from a hook in the ceiling when it is suddenly struck by a ball that is moving horizontally (see figure). The ball is covered with glue, so it sticks to the bar. During this collision 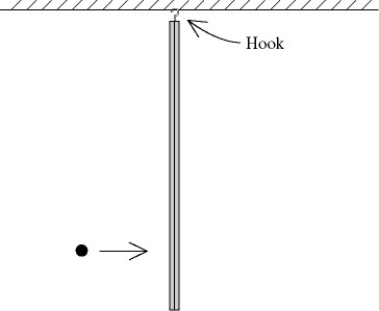
A) the angular momentum of the system (ball and bar) is conserved about the hook because only gravity is acting on the system.
B) the angular momentum of the system (ball and bar) is not conserved because the hook exerts a force on the bar.
C) the angular momentum of the system (ball and bar) is conserved about the hook because neither the hook nor gravity exerts any torque on this system about the hook.
D) both the angular momentum of the system (ball and bar) and its kinetic energy are conserved.
E) both the linear momentum and the angular momentum of the system (ball and bar) are conserved.

A) the angular momentum of the system (ball and bar) is conserved about the hook because only gravity is acting on the system.
B) the angular momentum of the system (ball and bar) is not conserved because the hook exerts a force on the bar.
C) the angular momentum of the system (ball and bar) is conserved about the hook because neither the hook nor gravity exerts any torque on this system about the hook.
D) both the angular momentum of the system (ball and bar) and its kinetic energy are conserved.
E) both the linear momentum and the angular momentum of the system (ball and bar) are conserved.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
11
A solid sphere, solid cylinder, and a hollow pipe all have equal masses and radii and are of uniform density. If the three are released simultaneously at the top of an inclined plane and roll without slipping, which one will reach the bottom first?
A) solid sphere
B) hollow pipe
C) solid cylinder
D) They all reach the bottom at the same time.
A) solid sphere
B) hollow pipe
C) solid cylinder
D) They all reach the bottom at the same time.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
12
The two rotating systems shown in the figure differ only in that the two identical movable masses are positioned at different distances from the axis of rotation. If you release the hanging blocks simultaneously from rest, and if the ropes do not slip, which block lands first? 
A) The block at the left lands first.
B) The block at the right lands first.
C) Both blocks land at the same time.

A) The block at the left lands first.
B) The block at the right lands first.
C) Both blocks land at the same time.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
13
The angular momentum of a system remains constant
A) when the total kinetic energy is constant.
B) when no net external force acts on the system.
C) when the linear momentum and the energy are constant.
D) when no torque acts on the system.
E) all the time since it is a conserved quantity.
A) when the total kinetic energy is constant.
B) when no net external force acts on the system.
C) when the linear momentum and the energy are constant.
D) when no torque acts on the system.
E) all the time since it is a conserved quantity.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
14
When a rigid body rotates about a fixed axis, all the points in the body have the same
A) tangential speed.
B) angular acceleration.
C) tangential acceleration.
D) linear displacement.
E) centripetal acceleration.
A) tangential speed.
B) angular acceleration.
C) tangential acceleration.
D) linear displacement.
E) centripetal acceleration.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
15
If 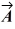 and
and 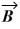
Are nonzero vectors for which
∙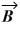
= 0, it must follow that
A)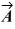 ×
× 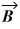 = 0.
= 0.
B)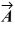 is parallel to
is parallel to 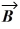 .
.
C) |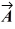 ×
× 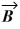 | = AB.
| = AB.
D) |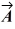 ×
× 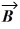 | = 1.
| = 1.
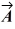 and
and 
Are nonzero vectors for which
∙
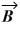
= 0, it must follow that
A)
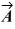 ×
×  = 0.
= 0.B)
 is parallel to
is parallel to 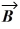 .
.C) |
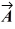 ×
× 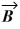 | = AB.
| = AB.D) |
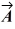 ×
×  | = 1.
| = 1.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
16
A uniform disk, a uniform hoop, and a uniform solid sphere are released at the same time at the top of an inclined ramp. They all roll without slipping. In what order do they reach the bottom of the ramp?
A) disk, hoop, sphere
B) hoop, sphere, disk
C) sphere, disk, hoop
D) sphere, hoop, disk
E) hoop, disk, sphere
A) disk, hoop, sphere
B) hoop, sphere, disk
C) sphere, disk, hoop
D) sphere, hoop, disk
E) hoop, disk, sphere

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
17
If an irregularly shaped object (such as a wrench) is dropped from rest in a classroom and feels no air resistance, it will
A) accelerate but will not spin.
B) accelerate and turn until its center of gravity reaches its lowest point.
C) accelerate and turn about its center of gravity with uniform angular speed.
D) accelerate and turn about its center of gravity with uniform angular acceleration.
E) accelerate and spin until its center of gravity reaches its highest point.
A) accelerate but will not spin.
B) accelerate and turn until its center of gravity reaches its lowest point.
C) accelerate and turn about its center of gravity with uniform angular speed.
D) accelerate and turn about its center of gravity with uniform angular acceleration.
E) accelerate and spin until its center of gravity reaches its highest point.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
18
If two vectors are perpendicular to each other, their cross product must be zero.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
19
A ball is released from rest on a no-slip surface, as shown in the figure. After reaching its lowest point, the ball begins to rise again, this time on a frictionless surface as shown in the figure. When the ball reaches its maximum height on the frictionless surface, it is 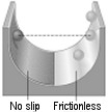
A) at a greater height as when it was released.
B) at a lesser height as when it was released.
C) at the same height as when it was released.
D) It is impossible to tell without knowing the mass of the ball.
E) It is impossible to tell without knowing the radius of the ball.

A) at a greater height as when it was released.
B) at a lesser height as when it was released.
C) at the same height as when it was released.
D) It is impossible to tell without knowing the mass of the ball.
E) It is impossible to tell without knowing the radius of the ball.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
20
Consider a uniform solid sphere of radius R and mass M rolling without slipping. Which form of its kinetic energy is larger, translational or rotational?
A) Its translational kinetic energy is larger than its rotational kinetic energy.
B) Its rotational kinetic energy is larger than its translational kinetic energy.
C) Both forms of energy are equal.
D) You need to know the speed of the sphere to tell.
A) Its translational kinetic energy is larger than its rotational kinetic energy.
B) Its rotational kinetic energy is larger than its translational kinetic energy.
C) Both forms of energy are equal.
D) You need to know the speed of the sphere to tell.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
21
A uniform solid sphere of mass M and radius R rotates with an angular speed ω about an axis through its center. A uniform solid cylinder of mass M, radius R, and length 2R rotates through an axis running through the central axis of the cylinder. What must be the angular speed of the cylinder so it will have the same rotational kinetic energy as the sphere?
A) 2ω/5
B)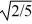 ω
ω
C) 4ω/5
D) 2ω/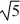
E) ω/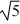
A) 2ω/5
B)
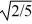 ω
ωC) 4ω/5
D) 2ω/
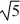
E) ω/
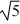

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
22
The angular acceleration of a wheel is given in rad/s2by 45t3 - 11t4, where t is in seconds. If the wheel starts from rest at t = 0.00 s, when is the next time the wheel is at rest?
A) 5.1 s
B) 8.4 s
C) 6.9 s
D) 3.6 s
A) 5.1 s
B) 8.4 s
C) 6.9 s
D) 3.6 s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
23
A machinist turns the power on to a grinding wheel, which is at rest at time t = 0.00 s. The wheel accelerates uniformly for 10 s and reaches the operating angular velocity of 25 rad/s. The wheel is run at that angular velocity for 37 s and then power is shut off. The wheel decelerates uniformly at 1.5 rad/s2 until the wheel stops. In this situation, the time interval of angular deceleration (slowing down) is closest to:
A) 17 s
B) 15 s
C) 19 s
D) 21 s
E) 23 s
A) 17 s
B) 15 s
C) 19 s
D) 21 s
E) 23 s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
24
A turbine blade rotates with angular velocity ω(t) = 2.00 rad/s- 2.1.00 rad/s3 t2. What is the angular acceleration of the blade at t = 9.10 s?
A) -38.2 rad/s2
B) -19.1 rad/s2
C) -86.0 rad/s2
D) -36.2 rad/s2
E) -172 rad/s2
A) -38.2 rad/s2
B) -19.1 rad/s2
C) -86.0 rad/s2
D) -36.2 rad/s2
E) -172 rad/s2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
25
In the figure, point P is at rest when it is on the x-axis. The time t, when P returns to the original position on the x-axis, is closest to 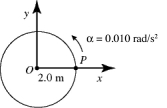
A) 13 s.
B) 18 s.
C) 25 s.
D) 35 s.
E) 50 s.

A) 13 s.
B) 18 s.
C) 25 s.
D) 35 s.
E) 50 s.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
26
The angular velocity of a 755-g wheel 15.0 cm in diameter is given by the equation ω(t) = (2.00 rad/s2)t + (1.00 rad/s4)t3.
(a) Through how many radians does the wheel turn during the first 2.00 s of its motion?
(b) What is the angular acceleration (in rad/s2) of the wheel at the end of the first 2.00 s of its motion?
(a) Through how many radians does the wheel turn during the first 2.00 s of its motion?
(b) What is the angular acceleration (in rad/s2) of the wheel at the end of the first 2.00 s of its motion?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
27
A uniform solid sphere has a moment of inertia I about an axis tangent to its surface. What is the moment of inertia of this sphere about an axis through its center?
A) 1/7 I
B) 2/7 I
C) 2/5 I
D) 3/5 I
E) 7/5 I
A) 1/7 I
B) 2/7 I
C) 2/5 I
D) 3/5 I
E) 7/5 I

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
28
A piece of thin uniform wire of mass m and length 3b is bent into an equilateral triangle. Find the moment of inertia of the wire triangle about an axis perpendicular to the plane of the triangle and passing through one of its vertices.
A)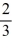 mb2
mb2
B) mb2
mb2
C)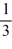 mb2
mb2
D)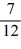 mb2
mb2
E) mb2
mb2
A)
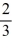 mb2
mb2B)
 mb2
mb2C)
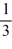 mb2
mb2D)
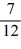 mb2
mb2E)
 mb2
mb2
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
29
A slender uniform rod 100.00 cm long is used as a meter stick. Two parallel axes that are perpendicular to the rod are considered. The first axis passes through the 50-cm mark and the second axis passes through the 30-cm mark. What is the ratio of the moment of inertia through the second axis to the moment of inertia through the first axis?
A) I2/I1 = 1.5
B) I2/I1 = 1.7
C) I2/I1 = 1.9
D) I2/I1 = 2.1
E) I2/I1 = 2.3
A) I2/I1 = 1.5
B) I2/I1 = 1.7
C) I2/I1 = 1.9
D) I2/I1 = 2.1
E) I2/I1 = 2.3

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
30
A futuristic design for a car is to have a large solid disk-shaped flywheel within the car storing kinetic energy. The uniform flywheel has mass 370 kg with a radius of 0.500 m and can rotate up to 230 rev/s. Assuming all of this stored kinetic energy could be transferred to the linear velocity of the 1600-kg\ car, find the maximum attainable speed of the car.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
31
A 4.50-kg wheel that is 34.5 cm in diameter rotates through an angle of 13.8 rad as it slows down uniformly from 22.0 rad/s to 13.5 rad/s. What is the magnitude of the angular acceleration of the wheel?
A) 0.616 rad/s2
B) 5.45 rad/s2
C) 111 rad/s2
D) 22.5 rad/s2
E) 10.9 rad/s2
A) 0.616 rad/s2
B) 5.45 rad/s2
C) 111 rad/s2
D) 22.5 rad/s2
E) 10.9 rad/s2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
32
When a 2.75-kg fan, having blades 18.5 cm long, is turned off, its angular speed decreases uniformly from 10.0 rad/s to 6.30 rad/s in 5.00 s.
(a) What is the magnitude of the angular acceleration of the fan?
(b) Through what angle (in degrees) does it turn while it is slowing down during the 5.00 s?
(c) If its angular acceleration does not change, how long after it is turned off does it take the fan to stop.
(a) What is the magnitude of the angular acceleration of the fan?
(b) Through what angle (in degrees) does it turn while it is slowing down during the 5.00 s?
(c) If its angular acceleration does not change, how long after it is turned off does it take the fan to stop.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
33
In the figure, a weightlifter's barbell consists of two identical uniform spherical masses each with radius 0.17 m and mass of 50 kg. The weights are connected by a 0.96-m uniform steel rod with a mass of 12 kg. Find the moment of inertia of the barbell about the axis through the center (see figure). 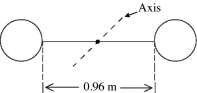


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
34
A 1.15-kg grinding wheel 22.0 cm in diameter is spinning counterclockwise at a rate of 20.0 revolutions per second. When the power to the grinder is turned off, the grinding wheel slows with constant angular acceleration and takes 80.0 s to come to a rest.
(a) What was the angular acceleration (in rad/s2) of the grinding wheel as it came to rest if we take a counterclockwise rotation as positive?
(b) How many revolutions did the wheel make during the time it was coming to rest?
(a) What was the angular acceleration (in rad/s2) of the grinding wheel as it came to rest if we take a counterclockwise rotation as positive?
(b) How many revolutions did the wheel make during the time it was coming to rest?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
35
While spinning down from 500.0 rpm to rest, a solid uniform flywheel does 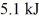 of work. If the radius of the disk is
of work. If the radius of the disk is 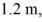
What is its mass?
A) 5.2 kg
B) 4.4 kg
C) 6.0 kg
D) 6.8 kg
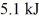 of work. If the radius of the disk is
of work. If the radius of the disk is 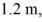
What is its mass?
A) 5.2 kg
B) 4.4 kg
C) 6.0 kg
D) 6.8 kg

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
36
A 1.25-kg ball begins rolling from rest with constant angular acceleration down a hill. If it takes 3.60 s for it to make the first complete revolution, how long will it take to make the next complete revolution?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
37
At any angular speed, a certain uniform solid sphere of diameter D has half as much rotational kinetic energy as a certain uniform thin-walled hollow sphere of the same diameter when both are spinning about an axis through their centers. If the mass of the solid sphere is M, the mass of the hollow sphere is
A) 3/5 M.
B) 5/3 M.
C) 5/6 M.
D) 6/5 M.
E) 2 M.
A) 3/5 M.
B) 5/3 M.
C) 5/6 M.
D) 6/5 M.
E) 2 M.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
38
In the figure, point P is at rest when it is on the x-axis. The linear speed of point P when it reaches the y-axis is closest to 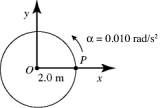
A) 0.18 m/s.
B) 0.24 m/s.
C) 0.35 m/s.
D) 0.49 m/s.
E) 0.71 m/s.

A) 0.18 m/s.
B) 0.24 m/s.
C) 0.35 m/s.
D) 0.49 m/s.
E) 0.71 m/s.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
39
A 3.45-kg centrifuge takes 100 s to spin up from rest to its final angular speed with constant angular acceleration. A point located 8.00 cm from the axis of rotation of the centrifuge moves with a speed of 150 m/s when the centrifuge is at full speed.
(a) What is the angular acceleration (in rad/s2) of the centrifuge as it spins up?
(b) How many revolutions does the centrifuge make as it goes from rest to its final angular speed?
(a) What is the angular acceleration (in rad/s2) of the centrifuge as it spins up?
(b) How many revolutions does the centrifuge make as it goes from rest to its final angular speed?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
40
An extremely light rod 1.00 m long has a 2.00-kg mass attached to one end and a 3.00-kg mass attached to the other. The system rotates at a constant angular speed about a fixed axis perpendicular to the rod that passes through the rod 30.0 cm from the end with the 3.00-kg mass attached. The kinetic energy of the system is measured to be 100.0 J.
(a) What is the moment of inertia of this system about the fixed axis?
(b) What is the angular speed (in revolutions per second) of this system?
(a) What is the moment of inertia of this system about the fixed axis?
(b) What is the angular speed (in revolutions per second) of this system?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
41
In the figure, two blocks, of masses 2.00 kg and 3.00 kg, are connected by a light string that passes over a frictionless pulley of moment of inertia 0.00400 kg · m2 and radius 5.00 cm. The coefficient of friction for the tabletop is 0.300. The blocks are released from rest. Using energy methods, find the speed of the upper block just as it has moved 0.600 m. 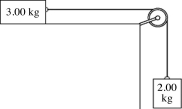
A) 1.22 m/s
B) 5.44 m/s
C) 3.19 m/s
D) 1.95 m/s
E) 1.40 m/s

A) 1.22 m/s
B) 5.44 m/s
C) 3.19 m/s
D) 1.95 m/s
E) 1.40 m/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
42
A thin cylindrical shell is released from rest and rolls without slipping down an inclined ramp that makes an angle of 30° with the horizontal. How long does it take it to travel the first 3.1 m?
A) 1.4 s
B) 1.1 s
C) 2.1 s
D) 1.6 s
E) 1.8 s
A) 1.4 s
B) 1.1 s
C) 2.1 s
D) 1.6 s
E) 1.8 s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
43
In an experiment, a student brings up the rotational speed of a piece of laboratory apparatus to 30.0 rpm. She then allows the apparatus to slow down uniformly on its own, and counts 240 revolutions before the apparatus comes to a stop. The moment of inertia of the apparatus is known to be 0.0850 kg∙m2. What is the magnitude of the retarding torque on the apparatus?
A) 0.0425 N∙m
B) 0.159 N∙m
C) 0.0787 N∙m
D) 0.000278 N∙m
E) 0.0000136 N∙m
A) 0.0425 N∙m
B) 0.159 N∙m
C) 0.0787 N∙m
D) 0.000278 N∙m
E) 0.0000136 N∙m

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
44
A solid uniform sphere of mass 1.85 kg and diameter 45.0 cm spins about an axle through its center. Starting with an angular velocity of 2.40 rev/s, it stops after turning through 18.2 rev with uniform acceleration. The net torque acting on this sphere as it is slowing down is closest to
A) 0.00593 N ∙ m.
B) 0.0372 N ∙ m.
C) 0.0466 N ∙ m.
D) 0.0620 N ∙ m.
E) 0.149 N ∙ m.
A) 0.00593 N ∙ m.
B) 0.0372 N ∙ m.
C) 0.0466 N ∙ m.
D) 0.0620 N ∙ m.
E) 0.149 N ∙ m.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
45
What is the torque about the origin on a particle located at
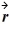
= 3 m
+ 4 m
- 2 m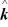
If a force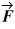
= 5 N
- 2 N
+ 3 N
Acts on the particle?
A) (8 +
+  - 26
- 26  ) N∙m
) N∙m
B) (8 - 19
- 19  - 26
- 26  ) N∙m
) N∙m
C) (8 + 2
+ 2  +
+ 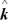 ) N∙m
) N∙m
D) (16 - 19
- 19  - 26
- 26 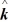 ) N∙m
) N∙m
E) (8 - 2
- 2  +
+ 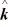 ) N∙m
) N∙m
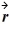
= 3 m

+ 4 m

- 2 m
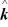
If a force
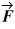
= 5 N

- 2 N

+ 3 N
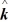
Acts on the particle?
A) (8
 +
+  - 26
- 26 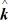 ) N∙m
) N∙mB) (8
 - 19
- 19  - 26
- 26 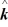 ) N∙m
) N∙mC) (8
 + 2
+ 2  +
+ 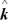 ) N∙m
) N∙mD) (16
 - 19
- 19  - 26
- 26 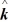 ) N∙m
) N∙mE) (8
 - 2
- 2  +
+ 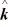 ) N∙m
) N∙m
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
46
A 95 N force exerted at the end of a 0.50 m long torque wrench gives rise to a torque of 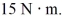 What is the angle (assumed to be less than 90°) between the wrench handle and the direction of the applied force?
What is the angle (assumed to be less than 90°) between the wrench handle and the direction of the applied force?
A) 18°
B) 14°
C) 22°
D) 25°
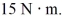 What is the angle (assumed to be less than 90°) between the wrench handle and the direction of the applied force?
What is the angle (assumed to be less than 90°) between the wrench handle and the direction of the applied force?A) 18°
B) 14°
C) 22°
D) 25°

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
47
A wheel has a radius of 0.40 m and is mounted on frictionless bearings. A block is suspended from a rope that is wound on the wheel and attached to it (see figure). The wheel is released from rest and the block descends 1.5 m in 2.00 s without any slipping of the rope. The tension in the rope during the descent of the block is 20 N. What is the moment of inertia of the wheel? 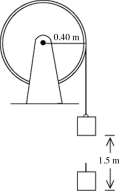
A) 3.5 kg · m2
B) 3.7 kg · m2
C) 3.9 kg · m2
D) 4.1 kg · m2
E) 4.3 kg · m2

A) 3.5 kg · m2
B) 3.7 kg · m2
C) 3.9 kg · m2
D) 4.1 kg · m2
E) 4.3 kg · m2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
48
A force 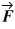 = 3.00 N
= 3.00 N 
- 2.00 N
Acts at a location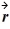
= 1.00 m
+ 2.00 m
On an object. What is the torque that this force applies about an axis through the origin perpendicular to the xy-plane?
A) -1.00 N∙m
B) 7.00 N∙m
C) -3.00 N∙m
D) 5.00 N∙m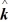
E) -8.00 N∙m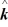
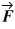 = 3.00 N
= 3.00 N 
- 2.00 N

Acts at a location
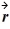
= 1.00 m

+ 2.00 m

On an object. What is the torque that this force applies about an axis through the origin perpendicular to the xy-plane?
A) -1.00 N∙m
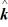
B) 7.00 N∙m
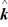
C) -3.00 N∙m
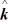
D) 5.00 N∙m
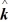
E) -8.00 N∙m

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
49
A very thin uniform rod, 2.40 m long and of weight 135 N, has a frictionless hinge at its lower end. It starts out vertically from rest and falls, pivoting about the hinge. Just as it has rotated through an angle of 55.0°, what is the downward acceleration of the end farthest from the hinge?
A) 5.02 m/s2
B) 8.03 m/s2
C) 9.80 m/s2
D) 12.0 m/s2
E) 19.6 m/s2
A) 5.02 m/s2
B) 8.03 m/s2
C) 9.80 m/s2
D) 12.0 m/s2
E) 19.6 m/s2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
50
A light triangular plate OAB is in a horizontal plane. Three forces, F1 = 6.0 N, F2 = 9.0 N, and
F3 = 7.0 N, act on the plate, which is pivoted about a vertical axes through point O. In the figure,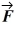
2 is perpendicular to OB. Consider the counterclockwise sense as positive. The sum of the torques about the vertical axis through point O, acting on the plate due to forces F1, F2, and F3, is closest to
A) 4.1 N ∙ m
B) 5.4 N ∙ m
C) -4.1 N ∙ m
D) -5.4 N ∙ m
E) zero
F3 = 7.0 N, act on the plate, which is pivoted about a vertical axes through point O. In the figure,
2 is perpendicular to OB. Consider the counterclockwise sense as positive. The sum of the torques about the vertical axis through point O, acting on the plate due to forces F1, F2, and F3, is closest to

A) 4.1 N ∙ m
B) 5.4 N ∙ m
C) -4.1 N ∙ m
D) -5.4 N ∙ m
E) zero

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
51
A torque of 12 N ∙ m is applied to a solid, uniform disk of radius 0.50 m, causing the disk to accelerate at 5.7 rad/s2. What is the mass of the disk?
A) 17 kg
B) 13 kg
C) 8.5 kg
D) 4.3 kg
A) 17 kg
B) 13 kg
C) 8.5 kg
D) 4.3 kg

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
52
A very thin horizontal, 2.00-m long, 5.00-kg uniform beam that lies along the east-west direction is acted on by two forces. At the east end of the beam, a 200-N force pushes downward. At the west end of the beam, a 200-N force pushes upward. What is the angular acceleration of the beam?
A) 240 rad/s2 north
B) 1.33 × 102 rad/s2 north
C) zero
D) 240 rad/s2 south
E) 1.33 × 102 rad/s2 south
A) 240 rad/s2 north
B) 1.33 × 102 rad/s2 north
C) zero
D) 240 rad/s2 south
E) 1.33 × 102 rad/s2 south

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
53
A 1.10-kg wrench is acting on a nut trying to turn it. The length of the wrench lies directly to the east of the nut. A force 150.0 N acts on the wrench at a position 15.0 cm from the center of the nut in a direction 30.0° north of east. What is the magnitude of the torque about the center of the nut?
A) 22.5 N∙m
B) 11.3 N∙m
C) 19.5 N∙m
D) 2250 N∙m
E) 1949 N∙m
A) 22.5 N∙m
B) 11.3 N∙m
C) 19.5 N∙m
D) 2250 N∙m
E) 1949 N∙m

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
54
A string is wrapped around a pulley with a radius of 2.0 cm and no appreciable friction in its axle. The pulley is initially not turning. A constant force of 50 N is applied to the string, which does not slip, causing the pulley to rotate and the string to unwind. If the string unwinds 1.2 m in 4.9 s, what is the moment of inertia of the pulley?
A) 0.17 kg∙m2
B) 17 kg∙m2
C) 14 kg∙m2
D) 0.20 kg∙m2
E) 0.017 kg∙m2
A) 0.17 kg∙m2
B) 17 kg∙m2
C) 14 kg∙m2
D) 0.20 kg∙m2
E) 0.017 kg∙m2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
55
For the apparatus shown in the figure, there is no slipping between the cord and the surface of the pulley. The blocks have mass of 3.0 kg and 5.7 kg, and the pulley has a radius of 0.12 m and a mass of 10.3 kg. At the instant the 5.7 kg mass has fallen 1.5 m starting from rest, find the speed of each block. (Assume the pulley is in the shape of a uniform solid disk and has no friction in its axle.) 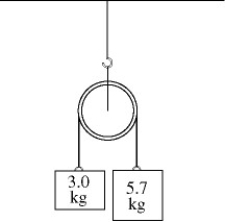


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
56
In the figure, a mass of 31.77 kg is attached to a light string that is wrapped around a cylindrical spool of radius 10.0 cm and moment of inertia 4.00 kg · m2. The spool is suspended from the ceiling, and the mass is then released from rest a distance 5.70 m above the floor. How long does it take to reach the floor? 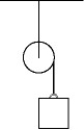
A) 3.98 s
B) 3.83 s
C) 1.14 s
D) 5.59 s
E) 7.89 s

A) 3.98 s
B) 3.83 s
C) 1.14 s
D) 5.59 s
E) 7.89 s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
57
In the figure, a very light rope is wrapped around a wheel of radius R = 2.0 meters and does not slip. The wheel is mounted with frictionless bearings on an axle through its center. A block of mass 14 kg is suspended from the end of the rope. When the system is released from rest it is observed that the block descends 10 meters in 2.0 seconds. What is the moment of inertia of the wheel? 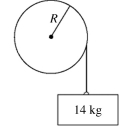


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
58
A 72.0-kg person pushes on a small doorknob with a force of 5.00 N perpendicular to the surface of the door. The doorknob is located 0.800 m from axis of the frictionless hinges of the door. The door begins to rotate with an angular acceleration of 2.00 rad/s2. What is the moment of inertia of the door about the hinges?
A) 4.28 kg∙m2
B) 7.52 kg∙m2
C) 1.88 kg∙m2
D) 0.684 kg∙m2
E) 2.74 kg∙m2
A) 4.28 kg∙m2
B) 7.52 kg∙m2
C) 1.88 kg∙m2
D) 0.684 kg∙m2
E) 2.74 kg∙m2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
59
A uniform solid cylindrical log begins rolling without slipping down a ramp that rises 28.0° above the horizontal. After it has rolled 4.20 m along the ramp, what is the magnitude of the linear acceleration of its center of mass?
A) 9.80 m/s2
B) 4.60 m/s2
C) 3.29 m/s2
D) 3.07 m/s2
E) 2.30 m/s2
A) 9.80 m/s2
B) 4.60 m/s2
C) 3.29 m/s2
D) 3.07 m/s2
E) 2.30 m/s2

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
60
The rotating systems shown in the figure differ only in that the two identical movable masses are positioned a distance r from the axis of rotation (left), or a distance r/2 from the axis of rotation (right). You release the hanging blocks simultaneously from rest, and call tL the time taken by the block on the left and tR the time taken by the block on the right to reach the bottom, respectively. The bar, pulley, and rope have negligible mass, the rope does not slip, and there is no friction in the axle of the pulley. Under these conditions 
A) tL = tR.
tR.
B) tL = tR.
C) tL =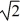 tR.
tR.
D) tL = 2tR.
E) tl = 4tR.

A) tL =
 tR.
tR.B) tL = tR.
C) tL =
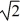 tR.
tR.D) tL = 2tR.
E) tl = 4tR.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
61
A uniform solid sphere of mass 1.5 kg and diameter 30.0 cm starts from rest and rolls without slipping down a 35° incline that is 7.0 m long.
(a) Calculate the linear speed of the center of the sphere when it reaches the bottom of the incline.
(b) Determine the angular speed of the sphere about its center at the bottom of the incline.
(c) Through what angle (in radians) does this sphere turn as it rolls down the incline?
(d) Does the linear speed in (a) depend on the radius or mass of the sphere? Does the angular speed in (b) depend on the radius or mass of the sphere?
(a) Calculate the linear speed of the center of the sphere when it reaches the bottom of the incline.
(b) Determine the angular speed of the sphere about its center at the bottom of the incline.
(c) Through what angle (in radians) does this sphere turn as it rolls down the incline?
(d) Does the linear speed in (a) depend on the radius or mass of the sphere? Does the angular speed in (b) depend on the radius or mass of the sphere?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
62
A uniform disk has a mass of 3.7 kg and a radius of 0.40 m. The disk is mounted on frictionless bearings and is used as a turntable. The turntable is initially rotating at 30 rpm. A thin-walled hollow cylinder has the same mass and radius as the disk. It is released from rest, just above the turntable, and on the same vertical axis. The hollow cylinder slips on the turntable for 0.20 s until it acquires the same final angular velocity as the turntable. What is the final angular momentum of the system?
A) 0.93 kg∙m2/s
B) 1.1 kg∙m2/s
C) 1.3 kg∙m2/s
D) 1.6 kg∙m2/s
E) 1.9 kg∙m2/s
A) 0.93 kg∙m2/s
B) 1.1 kg∙m2/s
C) 1.3 kg∙m2/s
D) 1.6 kg∙m2/s
E) 1.9 kg∙m2/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
63
A turntable has a radius of 0.80 m and a moment of inertia of 2.0 kg · m2. The turntable is rotating with an angular velocity of 1.5 rad/s about a vertical axis though its center on frictionless bearings. A very small 0.40-kg ball is projected horizontally toward the turntable axis with a velocity of 3.0 m/s. The ball is caught by a very small and very light cup-shaped mechanism on the rim of the turntable (see figure). The percent of the initial kinetic energy of the system that is lost during the capture of the ball is closest to 
A) 45%.
B) 51%.
C) 55%.
D) 60%.
E) 65%.

A) 45%.
B) 51%.
C) 55%.
D) 60%.
E) 65%.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
64
A 5.0-m radius playground merry-go-round with a moment of inertia of 2000 kg∙m2 is rotating freely with an angular speed of 1.0 rad/s. Two people, each having a mass of 60 kg, are standing right outside the edge of the merry-go-round and step on it with negligible speed. What is the angular speed of the merry-go-round right after the two people have stepped on?
A) 0.20 rad/s
B) 0.40 rad/s
C) 0.60 rad/s
D) 0.80 rad/s
E) 0.67 rad/s
A) 0.20 rad/s
B) 0.40 rad/s
C) 0.60 rad/s
D) 0.80 rad/s
E) 0.67 rad/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
65
A uniform solid sphere is rolling without slipping along a horizontal surface with a speed of 5.50 m/s when it starts up a ramp that makes an angle of 25.0° with the horizontal. What is the speed of the sphere after it has rolled 3.00 m up the ramp, measured along the surface of the ramp?
A) 4.01 m/s
B) 8.02 m/s
C) 1.91 m/s
D) 2.16 m/s
E) 3.53 m/s
A) 4.01 m/s
B) 8.02 m/s
C) 1.91 m/s
D) 2.16 m/s
E) 3.53 m/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
66
An 82.0 kg-diver stands at the edge of a light 5.00-m diving board, which is supported by two narrow pillars 1.60 m apart, as shown in the figure. Find the magnitude and direction of the force exerted on the diving board
(a) by pillar A.
(b) by pillar B.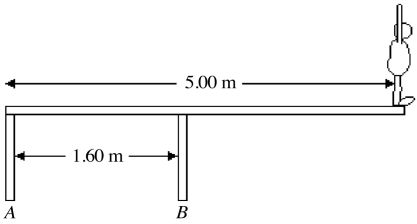
(a) by pillar A.
(b) by pillar B.


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
67
A solid, uniform sphere of mass 2.0 kg and radius 1.7 m rolls from rest without slipping down an inclined plane of height 7.0 m. What is the angular velocity of the sphere at the bottom of the inclined plane?
A) 5.8 rad/s
B) 9.9 rad/s
C) 11 rad/s
D) 7.0 rad/s
A) 5.8 rad/s
B) 9.9 rad/s
C) 11 rad/s
D) 7.0 rad/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
68
A lawn roller in the form of a uniform solid cylinder is being pulled horizontally by a horizontal force B applied to an axle through the center of the roller, as shown in the figure. The roller has radius 0.65 meters and mass 51 kg and rolls without slipping. What magnitude of the force B is required to give the center of mass of the roller an acceleration of 2.8 m/s2? 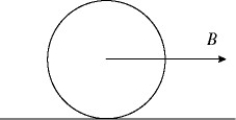


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
69
Three solid, uniform, cylindrical flywheels, each of mass 65.0 kg and radius 1.47 m rotate independently around a common axis. Two of the flywheels rotate in one direction at 3.83 rad/s; the other rotates in the opposite direction at 3.42 rad/s. Calculate the magnitude of the net angular momentum of the system.
A) 298 kg∙m2/s
B) 778 kg∙m2/s
C) 257 kg∙m2/s
D) 222 kg∙m2/s
A) 298 kg∙m2/s
B) 778 kg∙m2/s
C) 257 kg∙m2/s
D) 222 kg∙m2/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
70
A uniform hollow spherical ball of mass 1.75 kg and radius 40.0 cm rolls without slipping up a ramp that rises at 30.0° above the horizontal. The speed of the ball at the base of the ramp is 2.63 m/s. While the ball is moving up the ramp, find
(a) the acceleration (magnitude and direction) of its center of mass and
(b) the friction force (magnitude and direction) acting on it due to the surface of the ramp.
(a) the acceleration (magnitude and direction) of its center of mass and
(b) the friction force (magnitude and direction) acting on it due to the surface of the ramp.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
71
A uniform solid 5.25-kg cylinder is released from rest and rolls without slipping down an inclined plane inclined at 18° to the horizontal. How fast is it moving after it has rolled 2.2 m down the plane?
A) 4.3 m/s
B) 5.2 m/s
C) 3.0 m/s
D) 3.7 m/s
E) 2.6 m/s
A) 4.3 m/s
B) 5.2 m/s
C) 3.0 m/s
D) 3.7 m/s
E) 2.6 m/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
72
A figure skater rotating at 5.00 rad/s with arms extended has a moment of inertia of 2.25 kg∙m2. If the arms are pulled in so the moment of inertia decreases to 1.80 kg∙m2, what is the final angular speed?
A) 2.25 rad/s
B) 4.60 rad/s
C) 6.25 rad/s
D) 1.76 rad/s
E) 0.810 rad/s
A) 2.25 rad/s
B) 4.60 rad/s
C) 6.25 rad/s
D) 1.76 rad/s
E) 0.810 rad/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
73
A light board, 10 m long, is supported by two sawhorses, one at one edge of the board and a second at the midpoint. A small 40-N weight is placed between the two sawhorses, 3.0 m from the edge and 2.0 m from the center. What forces are exerted by the sawhorses on the board?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
74
A turntable has a radius of 0.80 m and a moment of inertia of 2.0 kg · m2. The turntable is rotating with an angular velocity of 1.5 rad/s about a vertical axis though its center on frictionless bearings. A very small 0.40-kg ball is projected horizontally toward the turntable axis with a velocity of 3.0 m/s. The ball is caught by a very small and very light cup-shaped mechanism on the rim of the turntable (see figure). What is the angular velocity of the turntable just after the ball is caught? 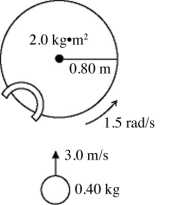
A) 2.1 rad/s
B) 1.3 rad/s
C) 0.94 rad/s
D) 0.75 rad/s
E) 0.30 rad/s

A) 2.1 rad/s
B) 1.3 rad/s
C) 0.94 rad/s
D) 0.75 rad/s
E) 0.30 rad/s

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
75
A uniform solid disk of radius 1.60 m and mass 2.30 kg rolls without slipping to the bottom of an inclined plane. If the angular velocity of the disk is 5.35 rad/s at the bottom, what is the height of the inclined plane?
A) 5.61 m
B) 4.21 m
C) 4.94 m
D) 6.73 m
A) 5.61 m
B) 4.21 m
C) 4.94 m
D) 6.73 m

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
76
A potter's wheel, with rotational inertia 46 kg∙m2, is spinning freely at 40 rpm. The potter drops a lump of clay onto the wheel, where it sticks a distance 1.2 m from the rotational axis. If the subsequent angular speed of the wheel and clay is 32 rpm what is the mass of the clay?
A) 8.0 kg
B) 5.4 kg
C) 7.0 kg
D) 8.8 kg
A) 8.0 kg
B) 5.4 kg
C) 7.0 kg
D) 8.8 kg

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
77
A 500-g particle is located at the point  = 4m
= 4m 
+ 3m
- 2m
And is moving with a velocity
= 5 m/s
-2 ms
+ 4 m/s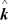
. What is the angular momentum of this particle about the origin?
A) (24 - 6
- 6  - 8
- 8 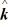 ) kg∙m2/s
) kg∙m2/s
B) (12 - 3
- 3  - 4
- 4 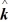 ) kg∙m2/s
) kg∙m2/s
C) (8 + 14
+ 14  - 13
- 13 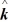 ) kg∙m2/s
) kg∙m2/s
D) (10 -
-  + 2
+ 2 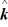 ) kg∙m2/s
) kg∙m2/s
E) (4 - 13
- 13  - 11.5
- 11.5 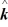 ) kg∙m2/s
) kg∙m2/s
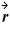 = 4m
= 4m 
+ 3m

- 2m
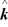
And is moving with a velocity
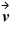
= 5 m/s

-2 ms

+ 4 m/s
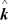
. What is the angular momentum of this particle about the origin?
A) (24
 - 6
- 6  - 8
- 8 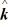 ) kg∙m2/s
) kg∙m2/sB) (12
 - 3
- 3  - 4
- 4  ) kg∙m2/s
) kg∙m2/sC) (8
 + 14
+ 14  - 13
- 13 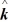 ) kg∙m2/s
) kg∙m2/sD) (10
 -
-  + 2
+ 2 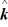 ) kg∙m2/s
) kg∙m2/sE) (4
 - 13
- 13  - 11.5
- 11.5 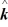 ) kg∙m2/s
) kg∙m2/s
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
78
A bicycle is traveling north at 5.0 m/s. The mass of the wheel, 2.0 kg, is uniformly distributed along the rim, which has a radius of 20 cm. What are the magnitude and direction of the angular momentum of the wheel about its axle?
A) 2.0 kg∙m2/s towards the west
B) 5.0 kg∙m2/s vertically upwards
C) 2.0 kg∙m2/s towards the east
D) 5.0 kg∙m2/s towards the east
E) 5.0 kg∙m2/s towards the west
A) 2.0 kg∙m2/s towards the west
B) 5.0 kg∙m2/s vertically upwards
C) 2.0 kg∙m2/s towards the east
D) 5.0 kg∙m2/s towards the east
E) 5.0 kg∙m2/s towards the west

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
79
A record is dropped vertically onto a freely rotating (undriven) turntable. Frictional forces act to bring the record and turntable to a common angular speed. If the rotational inertia of the record is 0.54 times that of the turntable, what percentage of the initial kinetic energy is lost?
A) 35%
B) 18%
C) 46%
D) 60%
A) 35%
B) 18%
C) 46%
D) 60%

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
80
A uniform solid cylinder of radius R and a thin uniform spherical shell of radius R both roll without slipping. If both objects have the same mass and the same kinetic energy, what is the ratio of the linear speed of the cylinder to the linear speed of the spherical shell?
A)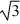 / 2
/ 2
B)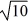 / 2
/ 2
C)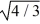
D) 4 /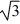
E) 4 / 3
A)
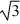 / 2
/ 2B)
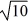 / 2
/ 2C)
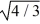
D) 4 /
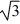
E) 4 / 3

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck


