Table 8-2 A Small Furniture Manufacturer Produces Tables and Chairs. Each Product

Multiple Choice

Table 8-2
A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 4 hours of assembly, 3 hours of finishing, and 1 hour of inspection. Each chair requires 3 hours of assembly, 2 hours of finishing, and 2 hours of inspection. The selling price per table is $140 while the selling price per chair is $90. Currently, each week there are 220 hours of assembly time available, 160 hours of finishing time, and 45 hours of inspection time. Assume that one hour of assembly time costs $5.00; one hour of finishing time costs $6.00; one hour of inspection time costs $4.50; and that whatever labor hours are not required for the table and chairs can be applied to another product. Linear programming is to be used to develop a production schedule. Define the variables as follows: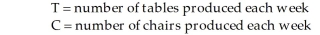
-According to Table 8-2, which describes a production problem, suppose you realize that you can trade off assembly hours for finishing hours, but that the total number of finishing hours, including the trade-off hours, cannot exceed 240 hours. How would this constraint be written?

A) 7T + 5C ≤ 360
B) 3T + 2C ≤ 240
C) 4T + 3C ≤ 140
D) −T − C ≤ 80
E) None of the above