TABLE 17-6 A Weight-Loss Clinic Wants to Use Regression Analysis to Build

Multiple Choice

TABLE 17-6
A weight-loss clinic wants to use regression analysis to build a model for weight loss of a client (measured in pounds) .Two variables thought to affect weight loss are client's length of time on the weight-loss program and time of session.These variables are described below:
Y = Weight loss (in pounds)
X₁ = Length of time in weight-loss program (in months)
X₂ = 1 if morning session,0 if not
X₃ = 1 if afternoon session,0 if not (Base level = evening session)
Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
Y = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₄X₁X₂ + β₅X₁X₃ + ε
Partial output from Microsoft Excel follows:
Regression Statistics 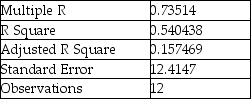ANOVA
F = 5.41118 Significance F = 0.040201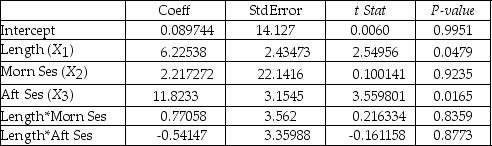
-Referring to Table 17-6,in terms of the βs in the model,give the mean change in weight loss (Y) for every 1-month increase in time in the program (X₁) when attending the evening session.

A) β₁+ β₄
B) β₁ + β₅
C) β₁
D) β₄ + β₅