Solved

Find a Geometric Power Series for the Function Centered at 0

Question 130

Multiple Choice

Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​ Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​ ​ A) B) C) D) E) ​


A) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​ ​ A) B) C) D) E)
B) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​ ​ A) B) C) D) E)
C) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​ ​ A) B) C) D) E)
D) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​ ​ A) B) C) D) E)
E) Find a geometric power series for the function centered at 0, (i) by the technique shown in Examples 1 and 2 and (ii) by long division. ​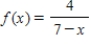 ​ A) 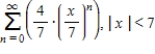B) 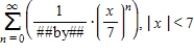C) 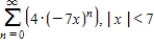D) 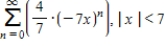E)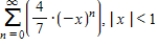

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q125: State where the power series <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg"

Q126: Determine the values of x for which

Q127: True or false: The series <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg"

Q128: Consider the sequence <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Consider the

Q129: Use the Integral Test to determine the

Q131: Which value is smaller, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Which

Q132: Use a power series to approximate the

Q133: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Consider the

Q134: Match the sequence with its graph. ​

Q135: Determine the convergence or divergence of the