The Number of Bacteria in a Culture Is Increasing According

Multiple Choice

The number of bacteria in a culture is increasing according to the law of exponential growth.After 5 hours there are 130 bacteria in the culture and after 10 hours there are 330 bacteria in the culture.Answer the following questions,rounding numerical answers to four decimal places. ​
(I) Find the initial population.
​
(II) Write an exponential growth model for the bacteria population.Let t represent time in hours.
​
(III) Use the model to determine the number of bacteria after 20 hours.
​
(IV) After how many hours will the bacteria count be 10,000?
​

A) (I) 51.2121 ; (II) 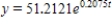; (III) 3,439.1838 ; (IV) 30.6439 hr
B) (I) 53.3621 ; (II) 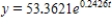; (III) 4,813.9010 ; (IV) 32.8719 hr
C) (I) 51.2121 ; (II) 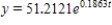; (III) 2,126.4497 ; (IV) 28.3094 hr
D) (I) 56.9921 ; (II) 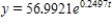; (III) 7,565.3544 ; (IV) 34.9831 hr
E) (I) 58.5521 ; (II) ; (III) 10,217.8179 ; (IV) 36.7625 hr