Solved

A Conical Tank (With Vertex Down)is 20 Feet Across the Top

Question 154

Multiple Choice

A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​


A) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E)
B) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E)
C) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E)
D) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E)
E) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. ​ A) B) C) D) E) A conical tank (with vertex down) is 20 feet across the top and 18 feet deep.If water is flowing into the tank at a rate of 20 cubic feet per minute,find the rate of change of the depth of the water when the water is 12 feet deep. 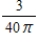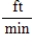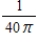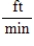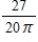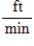​ A) B) C) D) E)

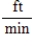
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q149: Differentiate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Differentiate with

Q150: An isosceles triangle is inscribed in a

Q151: Suppose that the total number of arrests

Q152: The radius of a right circular cylinder

Q153: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Evaluate for

Q155: Use Newton's Method to approximate the x-value

Q156: Find the derivative of the function <img

Q157: A population of 420 bacteria is introduced

Q158: Differentiate the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Differentiate the

Q159: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7497/.jpg" alt="Find by