Multiple Choice
What is an effective way of learning a complicated game such as chess? One recent study (de Bruin et al, 2007) had people learn using one of three methods: watching people play the game (the Watching condition) , watching and making predictions regarding what moves each player would do (the Predicting condition) , or watching and making predictions regarding what moves each player would do and explaining the reason for their prediction (the Explaining condition) . Later, each person played a series of games of chess against a computer and the percentage of time each person made correct moves was recorded; the higher the percentage, the better the player's ability to play chess. The researchers hypothesized that players who had to explain their predictions would have a higher ability than people who simply made predictions, who in turn would have a higher ability than those who simply watched others.
 You decide to conduct the analytical comparison of Watching vs. Predicting.
You decide to conduct the analytical comparison of Watching vs. Predicting.
In conducting this analytical comparison, how should the null and alternative hypotheses be stated?
A) H0: all μs are not equal; H1: not all μs are equal
B) H0: μWatching = μPredicting; H1: μWatching ≠μPredicting
C) H0: 1 ≠ 2; H1: 1 = 2
D) 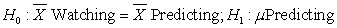
Correct Answer:

Verified
Correct Answer:
Verified
Q83: The Dunnett test is a statistical procedure
Q84: _ is the probability of making at
Q85: Which type of analytic comparisons is made
Q86: A one-way ANOVA is conducted comparing 6
Q87: The _ of the formula for the
Q89: The shape of the theoretical distribution of
Q90: Fred conducts a one-way ANOVA comparing five
Q91: Barney conducts a one-way ANOVA comparing the
Q92: If an F ratio is _ the
Q93: The likelihood of familywise error increases as