Solved

If the Lengths of Three Sides of a Triangle Are

Question 50

Short Answer

If the lengths of three sides of a triangle are known, then the following formula, known as Hero's (or Heron's) formula is sometimes used:
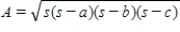​ If the lengths of three sides of a triangle are known, then the following formula, known as Hero's (or Heron's) formula is sometimes used: ​ ​​where a, b, and c are the given lengths of the sides, and . Use this formula to find the area of a triangle with the lengths given below (correct to the nearest square foot). 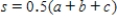​ , , and ​ __________ ft<sup>2</sup> ​​where a, b, and c are the given lengths of the sides, and If the lengths of three sides of a triangle are known, then the following formula, known as Hero's (or Heron's) formula is sometimes used: ​ ​​where a, b, and c are the given lengths of the sides, and . Use this formula to find the area of a triangle with the lengths given below (correct to the nearest square foot). ​ , , and ​ __________ ft<sup>2</sup> . Use this formula to find the area of a triangle with the lengths given below (correct to the nearest square foot).
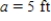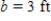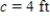
​ If the lengths of three sides of a triangle are known, then the following formula, known as Hero's (or Heron's) formula is sometimes used: ​ ​​where a, b, and c are the given lengths of the sides, and . Use this formula to find the area of a triangle with the lengths given below (correct to the nearest square foot). ​ , , and ​ __________ ft<sup>2</sup> , If the lengths of three sides of a triangle are known, then the following formula, known as Hero's (or Heron's) formula is sometimes used: ​ ​​where a, b, and c are the given lengths of the sides, and . Use this formula to find the area of a triangle with the lengths given below (correct to the nearest square foot). ​ , , and ​ __________ ft<sup>2</sup> , and If the lengths of three sides of a triangle are known, then the following formula, known as Hero's (or Heron's) formula is sometimes used: ​ ​​where a, b, and c are the given lengths of the sides, and . Use this formula to find the area of a triangle with the lengths given below (correct to the nearest square foot). ​ , , and ​ __________ ft<sup>2</sup> ​
__________ ft2

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q45: Consider the plot plan shown in the

Q46: Pick the best choice by estimating. Do

Q47: Find the perimeter by using the appropriate

Q48: If the lengths of three sides of

Q49: Pick the best choice by estimating. Do

Q51: Find the area of the shaded region.

Q52: The prefix centi- means _ (one thousand,

Q53: Name the metric unit you would use

Q54: Find the distance around the figure below

Q55: The perimeter <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7816/.jpg" alt="The perimeter