TABLE 14-15 the Superintendent of a School District Wanted to Predict the Predict

Multiple Choice

TABLE 14-15
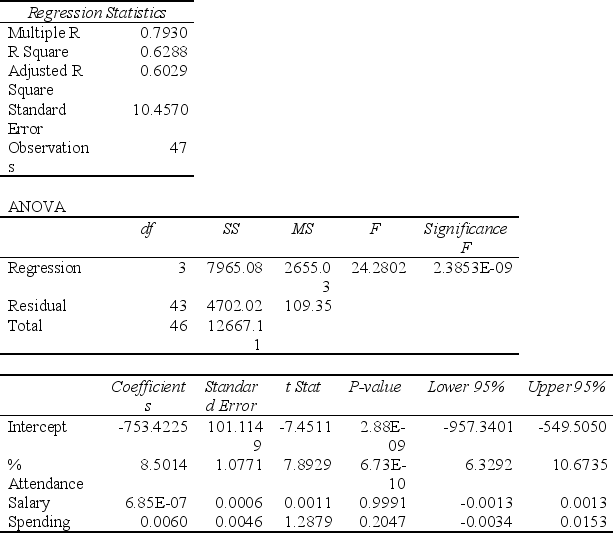
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing) , daily average of the percentage of students attending class (% Attendance) , average teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, X₁= % Attendance, X₂= Salaries and X₃= Spending:
Note:

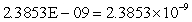
-Referring to Table 14-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?

A) H₁ : β₀ = β₁ = β₂ = β₃ ≠ 0
B) H₁ : β₁ = β₂ = β₃ ≠ 0
C) H₁ : At least one of β_j ≠ 0 for j = 0, 1, 2, 3
D) H₁ : At least one of β_j ≠ 0 for j = 1, 2, 3