Solved

Find the Fifth Roots of the Following Complex Number

Question 76

Multiple Choice

Find the fifth roots of the following complex number.Express the root(s) in trigonometric form. ​ Find the fifth roots of the following complex number.Express the root(s) in trigonometric form. ​ A) -3 B) C) D) E)


A) -3
B) Find the fifth roots of the following complex number.Express the root(s) in trigonometric form. ​ A) -3 B) C) D) E)
C) Find the fifth roots of the following complex number.Express the root(s) in trigonometric form. ​ A) -3 B) C) D) E)
D) Find the fifth roots of the following complex number.Express the root(s) in trigonometric form. ​ A) -3 B) C) D) E)
E) Find the fifth roots of the following complex number.Express the root(s) in trigonometric form. ​ A) -3 B) 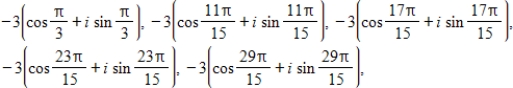C) 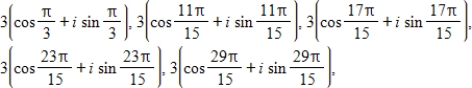D) E)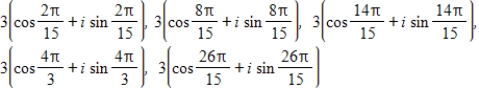

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q8: Raise the complex number to the fourth

Q24: Simplify the expression. ​<br>I <sup>-14</sup><br>​<br>A)i<br>B)-3i<br>C)-i<br>D)-1<br>E)1

Q71: Represent the complex number below graphically. <img

Q72: Use a graphing utility to represent the

Q73: Perform the addition or subtraction and write

Q74: Find the trigonometric form of the complex

Q78: Perform the operation and write the result

Q79: Use DeMoivre's Theorem to find the indicated

Q80: Use DeMoivre's theorem to find the indicated

Q81: Find a cubic polynomial function f with