Solved

Use the One-To-One Property to Solve the Following Equation for X

Question 197

Multiple Choice

Use the One-to-One Property to solve the following equation for x. Use the One-to-One Property to solve the following equation for x. A) B) C) D) E) 2


A) Use the One-to-One Property to solve the following equation for x. A) B) C) D) E) 2
B) Use the One-to-One Property to solve the following equation for x. 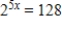A) 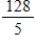B) 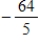C) 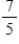D) 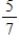E) 2
C) Use the One-to-One Property to solve the following equation for x. A) B) C) D) E) 2
D) Use the One-to-One Property to solve the following equation for x. A) B) C) D) E) 2
E) 2

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q5: Use the properties of logarithms to rewrite

Q192: Evaluate the logarithm using the change-of-base formula.Round

Q193: Sketch the graph of the function. ​

Q194: Find the magnitude R of an earthquake

Q196: Evaluate the function at the indicated value

Q198: Find the value of b that would

Q199: Write the logarithmic equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg" alt="Write

Q200: Rewrite the exponential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg" alt="Rewrite

Q201: Use the properties of logarithms to simplify

Q202: Solve the exponential equation algebraically.Approximate the result