Solved

Condense the Expression 3(log X - Log Y) to the Logarithm

Question 109

Multiple Choice

Condense the expression 3(log x - log y) to the logarithm of a single term.


A) Condense the expression 3(log x - log y) to the logarithm of a single term. A) B) C) D) 3(log x - log y) E)
B) Condense the expression 3(log x - log y) to the logarithm of a single term. A) B) C) D) 3(log x - log y) E)
C) Condense the expression 3(log x - log y) to the logarithm of a single term. A) B) C) D) 3(log x - log y) E)
D) 3(log x - log y)
E) Condense the expression 3(log x - log y) to the logarithm of a single term. A) 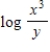B) 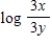C) 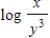D) 3(log x - log y) E)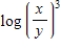

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q23: Find the exact value of the logarithmic

Q104: Solve the exponential equation algebraically.Approximate the result

Q106: Use the One-to-One Property to solve the

Q107: Identify the graph of the function. ​

Q108: Write the logarithmic equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7896/.jpg" alt="Write

Q110: What is the value of the function

Q111: Identify the x-intercept of the function <img

Q112: The population P (in thousands) of Orlando,

Q113: Write the exponential equation in logarithmic form.

Q114: Write the exponential equation in logarithmic form.